ガロア接続に基づく形式的概念分析の実験プログラム

Simple Program of Formal Concept Analysis
based on Galois Connection

by Akihiko Koga
30th Mar. 2021 (Update)
30th Mar. 2021 (First)

計算機（主にソフトウェア）の話題 へ
ホームページトップへ戻る

内容

  1. 趣旨
  2. 概略
  3. 動かしてみる
  4. いくつかの試行結果
  5. 考察
  6. プログラムの説明
  7. プログラムリスト
  8. 参考文献

趣旨

最近，別ページ

順序集合や束などに関する基本的な概念の説明
で，ガロア接続を詳しく説明しました．直接のリンクは
ガロア接続 (Galois Connection)
です．そのページを書いたとき，ガロア接続の応用として 形式的概念分析 のサンプルを作るために，Ruby でごく簡単なプログラムを作成しましたので， こちらにそのプログラムとそれを使ったいくつかの概念分析のサンプルを載せておきます．
2021.03.28 (日)

概略

ガロア接続は，二つの順序集合間である種の相互拘束がある状態で，その二つの順序集合の 間の共通の構造を浮かび上がらせることができます．形式的概念分析（Formal Concept Analysis）は， ガロア接続のこの特徴を，個体の集合とそれらの属性の集合の間にある関係に適用して， その関係から導出される概念を把握する目的に使うものです．

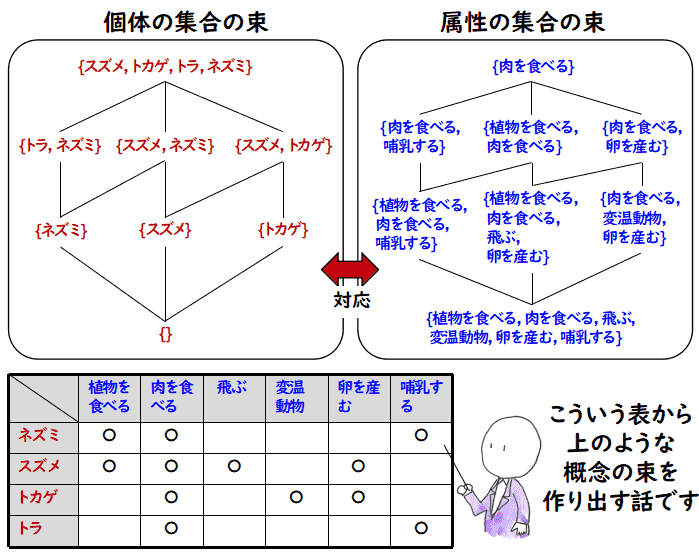
例えば，このページのオープニングの絵にあるように，

の間に，表
植物を食べる 肉を食べる 哺乳する 飛ぶ 卵を産む 変温動物
ネズミ 〇 〇 〇
スズメ 〇 〇 〇 〇
トカゲ 〇 〇 〇
トラ 〇 〇

で与えられるような関係が成立していたとしましょう．ガロア接続を使った形式的概念分析は この表から，

という概念の束（lattice）を作り出します．左は個体の集合間に包含関係で線を引いたもので， 右は属性の集合に逆の包含関係で線を引いたものです．この左右の束は対応しています．例えば，左側の 上から２番目の一番左には {トラ, ネズミ} があり，右側の対応する部分には {肉を食べる, 哺乳する} があります．これは，この表で，

ことを示しています．

この図で次の２つのことに注意してください．

  1. 個体側も属性側もすべての部分集合が列挙されている訳ではないこと

  2. 左右の束は同型で集合の包含関係は上下逆になっていること

一番目の項目について言えば，この例では個体は４つ，属性は６つありますから，個体の方の 部分集合の個数は 24=16個，属性の方の部分集合の個数は 26=64個 あるはずですが，左右とも 8 個ずつしか出てきていません．これは左右の対応において， お互いに相手側に含まれるものと与えられた表の関係になっているものすべて を列挙することにより，考える部分集合を減らすことができるからです．例えば，図の右側の 束で下から２番目の {植物を食べる, 肉を食べる, 飛ぶ, 卵を産む} は左側の {トリ} に 対応していますが，{トリ} を記述するだけなら，{飛ぶ} で良いはずです．しかし，ここでは 相手側の要素が共通に持っている属性すべてを列挙しています．このように対応する部分集合に 対して指定された表を満たす要素すべてを選び，それを標準的な対応とすることで，全部分集合を 考えないですむ訳です．

ここでもう一つ，{トラ} という部分集合が左の束に無いことに注意してください．「トラ」が 持っている属性は，{肉を食べる, 哺乳する} ですが，これを満たす左側の集合は {トラ, ネズミ} です．残念ながら，この，個体の集合も，属性の集合も最大化するという概念の表現体系では 「トラ」単独の集合は表すことができません．

二番目の項目について言えば，個体の数，属性の数が異なっていても，上のように表の関係を 満たすすべての要素を選ぶということで，左右がまったく同じ形になります．このとき， 図の線の意味は包含関係ですが，逆向きの包含関係になっていることに注意してください． 一般に，個体の集合が増えれば，それら共通の属性の個数は減り，また，属性の個数が 増えれば，それらを満足する個体の個数は減るのです．つまり，ガロア接続の概念束の 対応は上下の関係が逆になります．

これがガロア接続に基づく形式的概念分析のおよその内容ですが，詳しい話はこのサイトの 別ページ

ガロア接続 (Galois Connection)
を読んでください．

ここでは，上のように

を与えたとき，そこからガロア接続により抽出される概念の束を計算するごく簡単な プログラムを作成し，それを使っていくつかの例を見ていきます． ただし，ここではごくごく簡単なものを作るだけで，束の図を表示するような ものは作りません．単に，関係の表が与えられたとき，個体，属性でそれぞれどんな部分集合が この概念束に現れるかを計算するだけのプログラムです． 世の中にはすでにこの形式的概念分析のツールが色々出ているようです．それらのツールは 図を描いてくれたり，なにか高度な分析をしてくれたりするのだと思います．したがって， 皆さんはここで形式的概念分析がどんなものかを掴んだら，それらを調べて使ってみるのが 良いのではないでしょうか．

目次に戻る

動かしてみる

このプログラムは Ruby で作っています．このページの後ろの方の プログラムリスト にプログラムを掲載していますので，コピーしてファイルとして保存してください．ここでは "fca.rb" というファイルに保存したとします． 

c:\ruby\exper>irb                  # Ruby の対話的インタープリタ irb を起動します
irb(main):001:0> load "fca.rb"     # ファイル "fca.rb" をロードします
=> true
irb(main):002:0> fca($sample)      # $sample のデータから概念束を作ります
                                   # 以下がその結果です
----- Concept Lattice (Objects -> properties) -----
{スズメ, トカゲ, トラ, ネズミ}
 {肉を食べる}
{トラ, ネズミ}
 {肉を食べる, 哺乳する}
{スズメ, ネズミ}
 {植物を食べる, 肉を食べる}
{スズメ, トカゲ}
 {肉を食べる, 卵を産む}
{ネズミ}
 {植物を食べる, 肉を食べる, 哺乳する}
{トカゲ}
 {肉を食べる, 変温動物, 卵を産む}
{スズメ}
 {植物を食べる, 肉を食べる, 飛ぶ, 卵を産む}
{}
 {植物を食べる, 肉を食べる, 飛ぶ, 変温動物, 卵を産む, 哺乳する}
                                   # ここまでが概念束の出力です
=> [["スズメ", "トカゲ", "トラ", "ネズミ"], ["トラ", "ネズミ"], ["スズメ", "ネズミ"], ["スズメ", "トカゲ"], ["ネズミ"], ["トカゲ"], ["スズメ"], []]
irb(main):003:0>                   # 以上で終わりです

本プログラムの動かし方は上の通りです．掲載したプログラムリストの中には サンプルの表が $sample という大域変数に入っています．そのデータを

fca($sample)
のように，関数 fca() に入れて呼び出すだけです．

$sample の内容は次のような連想リストです． 

$sample = {
  "ネズミ" => ["哺乳する", "肉を食べる", "植物を食べる"],
  "スズメ" => ["卵を産む", "飛ぶ", "肉を食べる", "植物を食べる"],
  "トカゲ" => ["卵を産む", "肉を食べる", "変温動物"],
  "トラ"   => ["哺乳する", "肉を食べる"],
}

例えば，「ネズミ」が持つ属性を => の後ろにリストにして列挙してあるだけです． すべての個体のリストおよびすべての属性のリストは，この連想リストからプログラムが 集めます．

次に結果の見方を説明します．結果は次の部分です． 

----- Concept Lattice (Objects -> properties) -----
{スズメ, トカゲ, トラ, ネズミ}
 {肉を食べる}
{トラ, ネズミ}
 {肉を食べる, 哺乳する}
{スズメ, ネズミ}
 {植物を食べる, 肉を食べる}
{スズメ, トカゲ}
 {肉を食べる, 卵を産む}
{ネズミ}
 {植物を食べる, 肉を食べる, 哺乳する}
{トカゲ}
 {肉を食べる, 変温動物, 卵を産む}
{スズメ}
 {植物を食べる, 肉を食べる, 飛ぶ, 卵を産む}
{}
 {植物を食べる, 肉を食べる, 飛ぶ, 変温動物, 卵を産む, 哺乳する}

これは，次のように２行ずつ書いてあります．

個体の部分集合

対応する属性の集合

例えば，

{トラ, ネズミ}

{肉を食べる, 哺乳する}

というところがあると思いますが，これは個体の集合 {トラ, ネズミ} は 属性の集合 {肉を食べる, 哺乳する} に対応するということを表しています． 表示の順番は，集合の要素数の多い方から少ない方に表示しています． 属性の集合はこの逆ですね．属性の要素数の少ない方から多い方です．

ここで作ったプログラムの機能はここまでです．あとは一生懸命結果をパワーポイントなどで 図示してみてください．個体の束と属性の束は同型ですから，例えば，左右に分けるのではなく， 次の図のように，１つの束にして，そのノードの上下に個体の集合と対応する属性の集合を描くのでも 良いかなと思います．

目次に戻る

いくつかの試行結果

このツールは非常に単機能ですので，サンプルデータを変えてみるくらいしか 楽しみ方はありません．ということで，いくつかのサンプルでの実行結果を 載せておきます．あと，結果を図示するのは面倒ですので，プログラムの出力を ちょっとだけ読み易くするくらいでお許しください．あと，表も Web に貼るのに 自動生成したので， 属性の順番が機械任せで変なところもありますが，あまり気にしないようにしてください．

目次に戻る

考察

ここで作成したプログラムは形式的概念分析の原理を味合うのに本当に最小限のものでした． 多分，いくつかの例を自分で作ってみると次のような所が気になるのではないでしょうか？

自分で概念束を作ってみると，その他にも色々な気づきがあると思います． すでに世の中には，多くの形式的概念分析のツールがあるので，このような 点はいろいろな工夫があるのでしょう．興味がある人はそのようなツールを 調べてみるとよいでしょう．参考文献のところにも書きましたが， Wikipedia の formal concept analysis （英語版）の項目にはこのようなツールが いくつかあげてあるようです．

目次に戻る

プログラムの説明

Objects を個体の集合，Props を属性の集合とします．個体 x∈Objects に対して，x が 持つ属性の集合は f(x) で求められ，属性 y∈Prop に対して，その属性を持つ個体の集合は g(y) で求められるとします．

Objects : 個体の集合

Props : 属性の集合

f : Objects → P(Props)

f(x) は個体 x∈Objects が満たす属性の集合

g : Props → P(Objects)

g(y) は属性 y∈Props を持つ個体の集合

細かなことは省きますが，slist を属性 y∈Prop に対する g(y) すべてと Objects を 合わせた集合

slist := {g(y) | y∈Prop} ∪ {Objects}
slist は各属性 y∈Props に対して，その属性を満たす個体の集合 g(y) と 全個体の集合 Objects を合わせたもの
とするとき，slist から取って来た有限個の集合の交わりを求めていって， もう，これ以上新しい集合ができなくなったときのすべての集合が個体の束に 現れる個体の部分集合になります．疑似的なコードで書くと次のようになります． すなわち， slist の任意の２つの集合の交わりを作って次々に slist2 に入れていき， 新たに新しい集合が出来なくなったときに slist2 を結果とする訳です． 

    repeat {
      slist2 = {}
      for ∀x, ∀y∈slist do {
        slist2 = slist2 ∪ {x∩y}
      }
    } while (slist != slist2)

下に掲載したプログラムでは，連想リスト rel で与えられた個体と属性の関係から 逆の連想リスト rev を求めているので，slist は

[rel.keys.sort] | rel.values
で求めることができます．この式で | は集合の ∪ を表す Ruby の演算子です． sort しているのは集合としての等しさを判定しやすくするために，要素の順序を 標準化しているのです．

目次に戻る

プログラムリスト

ここで使っている簡易形式的概念分析のプログラムを次に掲載します． 各自でコピペして使ってください．こちらでは

で実行を確認しています．また，日本語は shift JIS を仮定しています． 

# -*- encoding: sjis
# Simple Formal Concept Analysis
#  Ver. 0.90 2021.03.29

$sample = {
  "ネズミ" => ["哺乳する", "肉を食べる", "植物を食べる"],
  "スズメ" => ["卵を産む", "飛ぶ", "肉を食べる", "植物を食べる"],
  "トカゲ" => ["卵を産む", "肉を食べる", "変温動物"],
  "トラ"   => ["哺乳する", "肉を食べる"],
}

def fca(rel)
  # make the reverse relation of rel
  rev = {}
  rel.keys.each {|k|
    rel[k] = rel[k].sort # standardize the order of elements in set
    rel[k].each {|p|
      rev[p] = (rev[p] == nil)?[k]:([k] | rev[p])
    }
  }
  rev.keys.each {|k|
    rev[k] = rev[k].sort  # standardize the order of elements in set
  }
  
  #  make the closure of the rel
  objects = fca_closure([rel.keys.sort] | rev.values)

  #  output the concept lattice
  printf("----- Concept Lattice (Objects -> properties) -----\n")
  objects.each {|u|
    fca_print_set("{", u, "}\n")
    v = rev.keys
    u.each {|y|
      v = v & rel[y]
    }
    fca_print_set(" {", v.sort, "}\n")
  }
end

def fca_closure(slist)
  slist2 = slist.map {|x| x.sort}
  begin
    slist = slist2
    slist.each {|x|
      slist.each {|y|
        z = (x & y).sort
        if !slist2.index(z) then
          slist2 = [z] + slist2
        end
      }
    }
  end until slist2 - slist == []
  slist.sort {|x, y| fca_compare(y, x)}
end

def fca_compare(x, y)
  if (x.length == y.length) then
    x.length.times {|i|
      if x[i] < y[i] then return -1
      elsif y[i] < x[i] then return 1
      end
    }
    return 0;
  else
    return x.length - y.length
  end
end

def fca_print_set(str1, x, str2)
  printf("%s", str1)
  n = x.length
  n.times {|i|
    printf("%s", x[i])
    if (i != n - 1) then printf(", ") end
  }
  printf("%s", str2)
end

目次に戻る

参考文献

ガロア接続に関する基礎や応用を勉強するのに有用な文献をあげておきます．

目次に戻る
計算機（主にソフトウェア）の話題 へ

圏論を勉強しよう へ
束論を勉強しよう へ
半群論を勉強しよう へ
ホームページトップ(Top of My Homepage)