以前,ある勉強会の発表用に集合論のサーベイ論文
を読んで,M. Randall Holmes, Thomas Forster, and Thierry Libert : ALTERNATIVE SET THEORIES, Sets and Extensoins in the Twentieth Century 2012, 74ページ
某勉強会で発表した「代替集合論」の発表資料に纏めました.
その中で
そういう状態だったのですが,どういう訳か,
最近,選択公理が
ということです.つまり,
あるいは,次のように閉集合の有限和は閉集合になりますが,無限和はどうなるか分からないと いう状況にも似ています.
その直観ををきちんと展開してみようと思ったので,まずは,その独立性の証明を思い出して 見ようと思い,その勉強会の発表資料を引っ張り出してきて読みなおしました. せっかく読んだので,もう一度,そこを纏め直すと理解が進むかなと思い,この ページを書いています.
ということで,ここでは
上のこと(選択公理と√2)に興味のない人も,一応,このページの内容は,ZFA と 選択公理の否定が無矛盾であることの簡単な解説になっているハズなので,お勉強には 役に立つと思います.ただし,「ZFA に選択公理の否定の追加が無矛盾なこと」であって 「ZF に選択公理の否定の追加が無矛盾なこと」ではありません.後者は証明に forcing を 使う必要がでてくるらしいです.前者はかなり簡単です.
これから ZFC, ZFA, そして,ZFA + ¬選択公理のモデルの説明をしますが, 読者は,1階述語論理とモデルについては知っているものとして話を進めます. もしご存じなければ,
に簡単に書いたものがありますので,参照してみてください.
まず,ZFC から思い出します.ZFC の公理は,公理スキームという形では,10個くらいの ものなのですが,たかが 10 個,されど 10 個で,慣れないうちは, なかなか全部をすぐ頭に思い浮かべることができません.何しろ,それで,現代数学を 全部導出できる訳ですから.
それで,私は次のように ZFC の公理系をとらえることにしています(私のとらえ方ですから,一般的な捉え方ではありません).
それは,公理的集合論 ZFC は,上の図のように,4方向から取り囲む公理群
∀A, B (A=B ↔ ∀x (x∈A ↔ x∈B))
x ∪ {x} を x+1 と表すことにします.(x+1)+1 を x+2, (x+2)+1 を x+3,以下同様です.
{x, y} は ∀u(u∈{x, y}→u=x ∨ u=y) を満たす集合です.この公理はそのような集合が存在することを保証します. 存在すれば,これは外延性公理から一意に決まります.
また,この対を作る機能を使って順序対 (x, y) を作ることができます.
を(x, y) := {{x, x}, {x, y}} = {{x}, {x, y}}
(u, v) = (x, y) ↔ (u=x ∧ v=y)を満たします.
∪ x := {u| ∃y∈x, u∈y}です.
2x := {y | y⊆x}
y⊆x ↔ ∀u (u∈y → u∈x)
です.
ここで,u∈X と u の範囲を限定しているのがミソです.
これが無いもの,つまり,
置換公理は,巨大な集合を作っていくときとても便利です.我々は無限集合
ω = {∅, ∅+1, ∅+2, ...}を持っていますが,実は,
ω2 := {ω, ω+1, ω+2, ...}さえ置換公理なしでは作ることができません.φ(u, v) := v=ω+u とすると,φ は関数性を有します.従って,置換公理から
ω2 := {v | φ(u, v) u∈ω}のように集合 ω2 を作ることができます.
ωn+1 := {ωn, ωn+1, ωn+2, ...} として,
{ω = ω1, ω2, ...}を作ることはできるでしょうか.
再帰を使っては作ることができますから,とにかく出来るのはできます. もっと簡単に出来ることを言えるかどうかは今思いつきません. でも,とにかく出来ることは出来るのです.
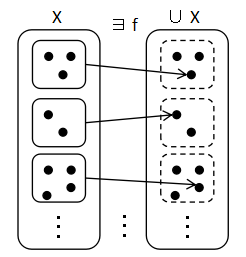 集合 X が空集合でなく,また,X のどの要素の集合も空集合で無いなら,
それらの集合から1つずつ要素を選ぶ関数があるということです.そのような
関数を
集合 X が空集合でなく,また,X のどの要素の集合も空集合で無いなら,
それらの集合から1つずつ要素を選ぶ関数があるということです.そのような
関数を
f(u)∈u for ∀u∈Xとなります.これは,∀u∈X から1つずつ要素を取って来た集合 C が 存在すると言っても同じです.そのような集合をここでは
|C ∩ u| = 1 for ∀u∈Xです.ただし,集合 S に対して,|S| でその要素数を表すことにします.
ここまでの説明は,|S| など,若干,未定義な用語を使ったりして,公理的な 扱いとしては荒っぽいところはあるとは思いますが,|S|=1 は
S≠∅ ∧ ∀x ∀y (x∈S ∧ y∈S →x=y)など,厳密に論理式で書けるということで勘弁してください.私は やはり直観的なイメージが無いと書き辛いので.
直観的には,集合 X には,無限に∈を下に辿っていける鎖
は無いと言う公理です.ここまで集合の包含関係を ∈ としてきましたので, 左側に ... がありますが,逆の包含関係 ∋ を使って...x2∈x1∈x0∈X
と書いた方が分かりやすいかもしれません.とにかく,そういう無限降下列が無いと いう公理です.X∋x0∋x1∋x2∋...
底に関する規定は,通常,次のような分かりにくい論理式で規定します.
Axiom of Regularityこれで ∈ の無限降下列を防げることを見て取るのは難しいのですが,例えば, X∈X という状況の起きる集合 X があったとすると,B:={X} という集合を考えれば B には X という要素しかない訳ですから,B∩X={X}∩X で,X∈X ならば, B∩X={X}≠∅ となり,この公理に反します.∀ A (A ≠ ∅ => ∃ X ∈ A (X ∩ A = ∅))
(空でない集合は自分自身とまじわりの無い要素を1つは持つ)
この形をよく使うのは,順序数として,Von Neumann 順序数を使った場合,集合に 含まれる順序数の最小値が,この全体の集合との交わりが ∅ の集合として 与えられるという恩恵があるからのようです. これらについては別ページ集合論:正則性 (Regularity)に少し詳しく説明しています.
上に ZFC の説明をしました.ZFC では,∅ だけが要素を持たない「もの(集合)」でした. ZFA は,集合以外のもの,アトムを許した集合論です.アトムは,どんな要素も含んでいない「もの」です.ZFA では,集合とアトムを区別するために,set(_) という述語を導入します. set(X) は X が集合であるときだけ成り立つ述語を意図しています.
ZFA の公理系は,ZFC の公理の内,外延性公理を次のように集合についてだけ成立するように弱めたものです.
弱外延性公理選択公理も一応抜いておきます.後で,ZFA に選択公理の否定を追加した公理系のモデルを 作るとき,邪魔になりますから.
∀A ∀B( set(A) ∧ set(B) → (A=B ↔ ∀x (x∈A ↔ x∈B)))
ZFA のイメージとしては,
のような感じです.空集合 ∅ や {∅}, {∅, {∅}} と言った,ZFC に 現れる集合があり,また,ZFA は,∅ の他にも,要素を含まないアトムが存在する世界です.図では アトム全体を A と書いています.A の要素は他の集合の要素になることができます.図では, アトム a を含む集合 {a, ∅} などが書かれています.
我々が学校ではじめて集合論を習うときのイメージがこういうものだと思います.
ここでは,ZFA のモデルを加工して,ZFA + ¬選択公理 のモデルの構築が作れることを 説明します.
まず,ZFA + ¬ 選択公理 のモデル作成の概要を説明します.これは 概要ではありますが,実のところ,殆どこの説明で,説明は終わっています. 次の図が.そのモデルの作り方と,そのモデルで選択公理が成り立たないことがあることの 証明の概略を表しています.
まず,前提として,
ここで,M の部分集合で,M' の要素にするための条件を記述するための用語を定義します.
B⊆M が,A の中の有限個の要素の集合 S⊆A を固定した全単射 φ に対しては
φ*(B)=B となるとき,B は
ZFA + ¬ 選択公理 のモデル (M', ∈) は次のように作ります.
です.M' :={B⊆M |ある有限集合 S⊆A が存在して,S の要素を動かさない φ に対して φ*(B)=B}
あとは,この (M', ∈) で選択公理が成り立たないことがあることと,(M', ∈) が ZFA になっていることを言えば良い訳です.
次に,(M', ∈) が
以上が,ZFA + ¬ 選択公理 のモデル (M', ∈) の構築と,そこで選択公理が 成り立たないことの証明の概略です.
ほぼ,これで全部のような気はするのですが,以下に,細かな用語の定義などを きちんとしておきます.
ZFA にモデル (M, E) があったとします.また,そのアトムの集合を A として,さらに A は無限集合であるとします.そのような ZFA のモデルがあったとするということです.
A から A への全単射 φ があったとき,これを M の部分集合に作用させる関数 φ* に 拡張する方法を説明します.
φ : A → A を A から A の全単射(bijection)とします.
このφ の B⊆M に対する拡張 φ*(B) を次の図のように定義します.
つまり,B の中のどの階層でも A の元 u が現れたら,それを φ(u) に置き換える訳です.ここでは直観的にだけ φ* を定義しておきます.ただし,これが定義できるのは ZFA に底に関する規定,つまり,∈ の無限降下列がないことを使っていることを注意しておきます.
B⊆M とします.
集合
B が |S|<∞ の support を持つとき,B は
B に A の要素が有限個しか現れなければ,それらを固定した全単射 φ に 対して,φ*(B)=B ですから,B は有限の support を持ちます.特に,∅ は 有限の support ∅ を持ちます.
この準備のもとに,「ZFA + ¬ 選択公理」のモデルを作ります.これは permutation model と 呼ばれます.自分自身への全単射は permutation とも呼ばれるからです.
今,(M, E) を ZFA のモデルで,そのアトムの集合 A⊆M は無限集合であるものとします.
このとき,モデル (M', ∈) を次のように作成します.
M' には,空集合 ∅ や無限集合 ω が入っています.また,アトムの 集合 A もどのような全単射 φ : A → A に対しても φ*(A)=A ですから, M' に含まれています.
選択公理が成り立つとすると,任意の集合の上に整列順序がある訳で, アトムの集合 A は M' に入っていますから,A の上に整列順序を定義できないと いけません.このような整列順序の一つを WA とすると,これは全順序にも なっています.WAは M' に入っていますから,有限の support があるはずです. それを S とします.A は無限集合ですから,S - A は二つの異なる要素を持っています. それを a と b とします.A→A の全単射 φ として,この a と b を入れ替える全単射を とると,これは S の要素を入れ替えませんが,WAは全順序ですから,(a, b) あるいは (b, a) のいずれか一方だけを含んでいたはずですから,φ*(WA) でこれが入れ替わってしまい,WAと一致しません.従って,WA は M' には入っておらず, 選択公理が成り立つと言う仮定に矛盾してしまいます.
(M', ∈) が ZFA のすべての公理を満たすことを示さなければなりません.
∅∈M' は簡単に言えます.A の要素を含まないのですから,support は ∅ で良い訳です.
新しい集合を生成する公理の,基本的なもの
上の「...と思います」も含めて,今はここに書く心理的な余裕がないので, とりあえず,先人の言を信じておくことにします.そのうち,元気がでたら,ここにも 証明を書くかもしれません.
上の説明では,選択公理が成り立たないことをいうのに,
新しい ZFA のモデル (M', ∈) で選択公理が成り立っていれば,その中にある集合 A の整列順序が あるはずだが,これは M' にないという持って回った説明でした.ここを改定して,私は,もっと直接的に,
ある集合 X の選択集合 C は存在しませんと言えないかなと思いました.持って回った言い方を避けるだけでなく,このページの 最初に書いていたように,
いろいろ考えた結果,次の集合の選択集合は存在しないのではないかと思います.
これは,A の任意の2要素 a, b に対して,(a, b) とその順序を逆にした (b, a) のペアからなっていますから, どのような全単射 φ : A → A に対しても変化しません.従ってXA := {{(a, b), (b, a)} | a, b∈A}
では,XA の選択集合はどうでしょう? XA の各要素は集合で,どれも 空集合ではありません.この選択集合のうち,ある集合を CA とします.CA は,任意の a, b∈A に対して,(a, b) か, あるいは,(b, a) かのどちらか一方だけを含んでいます.
CA に有限の support が存在するでしょうか.そのような support を S と してみます.そうすると,A - S は無限集合ですから,最低でも2つの異なる要素 a と b を 含んでいます.これを入れ替える全単射 φ を取ると,CA の中の,a と b の 順序対は前後が入れ替わりますから,φ*(CA)≠CA で,これは M' には入っていません.
こちらの説明の方が,選択公理が成り立つとして,整列順序が存在するという矛盾を導くより 直接的な説明かなと思います.また,この XA の選択集合の一つが整列順序であり, 全順序ですね. A の選択集合 CA は,選択の仕方によっては全順序じゃないかもしれませんが, これも上の説明の通り,M' には存在できません.
一応,上の説明は正しいとは思うのですが,やはり,人間のやることですし, 特に私だし,最近,ミスが多いので,「証明」という言葉を使うのが憚られて, 「説明」と言っています.変ですけど.
上の説明で,より直接的に,この集合の選択集合は無いという格好にしたので,とりあえず,ZFA + ¬選択公理 の permutaion model の作り方を復習したので, 「選択公理と √2 の類似性」の考察に入ります.
ZFA のモデル (M', ∈) では,
XA := {{(a, b), (b, a)} | a, b∈A}の
いま,アトムの集合 A の有限部分集合を A1 ⊆ A2 ⊆ A3 ⊆ ... ⊆ A のように 取って行ったとします.
XAi := |{(a, b), (b, a)} | a, b ∈ Ai}と置くと,XAi には選択集合があるのに,XAにはありません.
このページの先頭では √2 の近似を,実はニュートン法でやって言っていました. 分母分子がいくらでも大きくなっていく様子を表現したかったからです.でも,選択公理 との関係で言うと,10進数の小数で各桁を 0, 1, ..., 9 から選ぶようにした方がよいかも しれません.それで,この二つを対比させてみます.
今度はかなり類似性が明確になってきたと思います
しかし,この図を描いているとき,嫌なことを思い出しました.√2 の 場合は各桁は,{0, 1, 2, ..., 9} から選択する必要はなく,桁により一意に 決まるのです.従って,選択する必要はなく,せっかく近寄っていたイメージが また無関係になってしまいました.
上で,√2 の場合は,各桁が一意に決まり,選択の必要が無いので,√2 との類似性は特に言えないのですが,選択が必要な 任意の無理数とは,この類似性があるように思います.従って, 「ZFA+¬選択公理」と「有理数や代数的数の集合」の対応がなんとなく言えるのでは ないでしょうか.
集合,位相,論理など へ
圏論を勉強しよう へ
束論を勉強しよう へ
半群論を勉強しよう へ
ホームページトップ(Top of My Homepage)