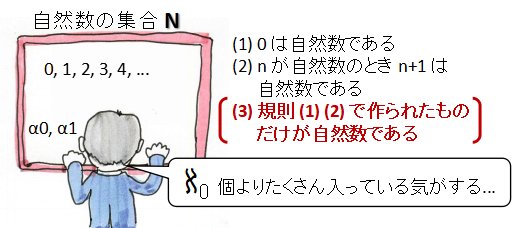
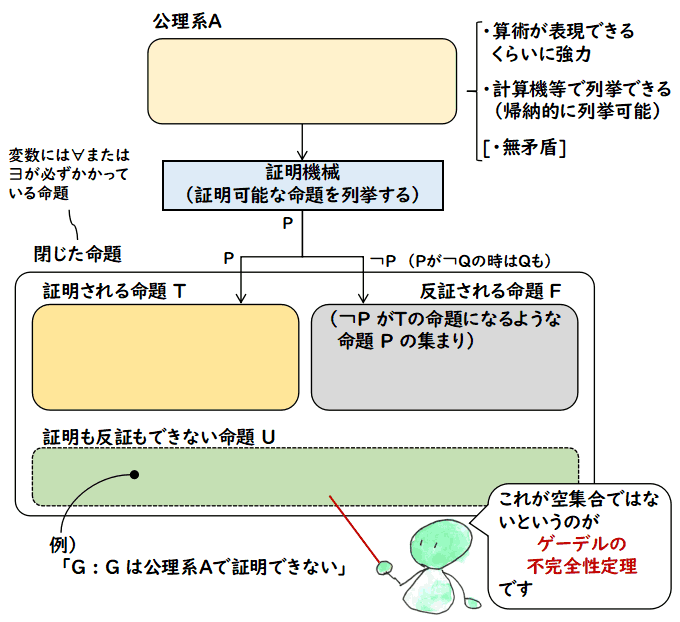
きちんとした公理的集合論の教科書の情報でも書けば良いのでしょうが, なんとなく,たまたま読んだ本や論文の情報を書いていきます.以下,素朴集合論, 圏論ベースの集合論,そのほかの項目も同様です.
Jaroslav Ježek : UNIVERSAL ALGEBRA, 2008, Chapter 1 Set Theory, pp. 3-22
これは普遍代数 (Universal Algebra) の教科書で PDF でダウンロードできます. URL は書かないので,上のタイトルと著者に PDF 位を入れて検索してください.本全体は227ページの普遍代数の本なのですが,
その第1章として,集合論が公理的に 導入してあります. 第1章の章始めには次のような説明があります.数学は集合論の上に築かれているが,直観的な集合論は 簡単にパラドックスに導かれてしまう.したがって,ここでは注意深く 集合の公理を選んだシステムを導入する.このようなシステムとしては,
とのことです.Gödel-Bernays のシステムとZermelo-Fraenkel のシステムがあるが Gödel-Bernaysのシステムの方が普遍代数に便利なのでそれを導入する
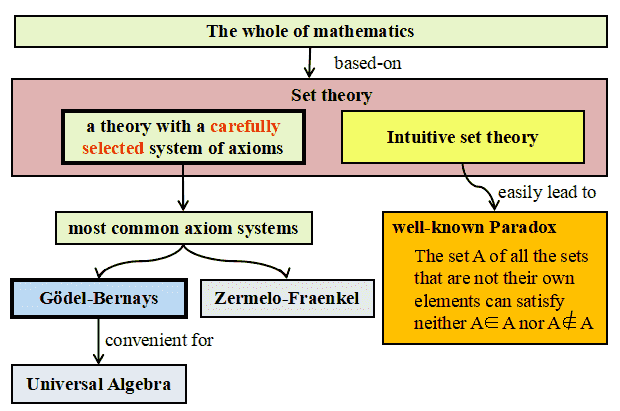
論理システムとしては,クラスまで含んだ公理系が記載されており, その中で何かの要素になっているものが集合で,そうでないものが純粋な クラスという具合に概念を定めています.
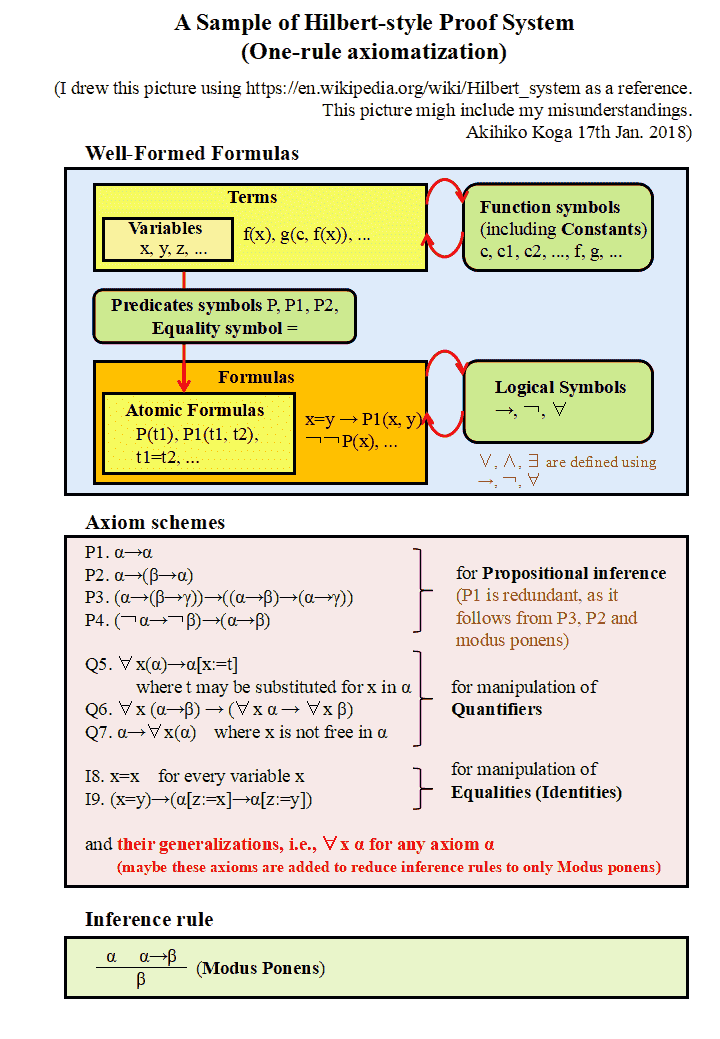
一応,このテキストで導入された公理系の概要を図にしておきます.
公理系は3段階あります.一番下が述語論理の公理系です注意1).ここで一通りの 論理的推論が可能になります.そして,その上にクラスの公理が9個置かれています. それぞれの公理のおよその役割は 図の中に書きました.ここではすべての集合のクラスは設けられていますが, すべてのクラスを集めたものはありません.このようにしてクラスの性質が 規定された後,最後に集合の公理が6個設けられています.正確な論理式は Ježek のテキスト(PDF)を参照してください.
この章の節は次の通りです.
- Formulas of set theory
- Theory of classes
- Set theory
- Relations and functions
- Ordinal numbers
- Cardinal numbers
- Comments
注意1) このテキストでは,述語論理(+ 等号(=)とメンバーシップ関係(∈))の公理が 15 個と推論規則が2個導入されています. ただ,p 4 の下の方に導入されている推論規則の2番目は私には怪しげに見えます. その規則は
(2) obtain f from (∀x)f
と書いてあるので,全称記号を外す推論規則のようですが,これは逆に 全称規則をつける推論規則が必要な気がします.著者が書き間違えたのでは ないでしょうか(2018年3月8日時点).追伸:知り合いとも話し合ってみた結果,ここはほぼ確実に 書き間違えだということになった.したがって,正しくは
と思われる.ただし,最終的な判断は読者自ら行ってほしい(2018年3月19日).(2) obtain (∀x)f from f
上の Jaroslav Ježek の普遍代数の本では, Gödel-Bernays のシステムとして紹介されていましたが, Wikipedia には von Neumann-Bernays-Gödel と3人の名前がついたシステムとして紹介されています(2018 年 1 月 19 日時点の英語版 Wikipedia).3人の貢献の内容,そして,その後のクラスに関する表現力を 強化した Morse-Kelley の体系など,結構分かりやすく書かれていました.ただ,細かな公理の 内容は違うようです(こういうの,標準的な公理系が欲しいな.あるいは,それぞれの公理系に 固有名詞がついていて,名前をあげれば公理系が一意に決るとか).
Ježek のところでも書きましたが,この公理系はすべての集合のクラスは導入されていますが, それ以上の集まり,たとえば,すべてのクラスの集まりは導入されていません(集合の圏は 記述できても圏の圏は無理ということかな).ということで, この体系は2種類の批判があるそうです.一つは強すぎるという批判で, もう一つは弱すぎる(不十分)という批判だそうです.世の中,なかなか,ままなりませんね(^_^)).
一般的に公理的集合論と言えばこちらのことみたいです (2018年1 月 19 日時点),こちらはクラスは定義されていません.ということで,上に書いた Gödel-Bernays より表現力は弱いのですが,記述を集合に限ると同じ定理が導出できるそうです.ここらあたりは,Wikipedia に分かりやすく書かれていました(2018 年 1 月 19 日時点の英語版 Wikipedia).
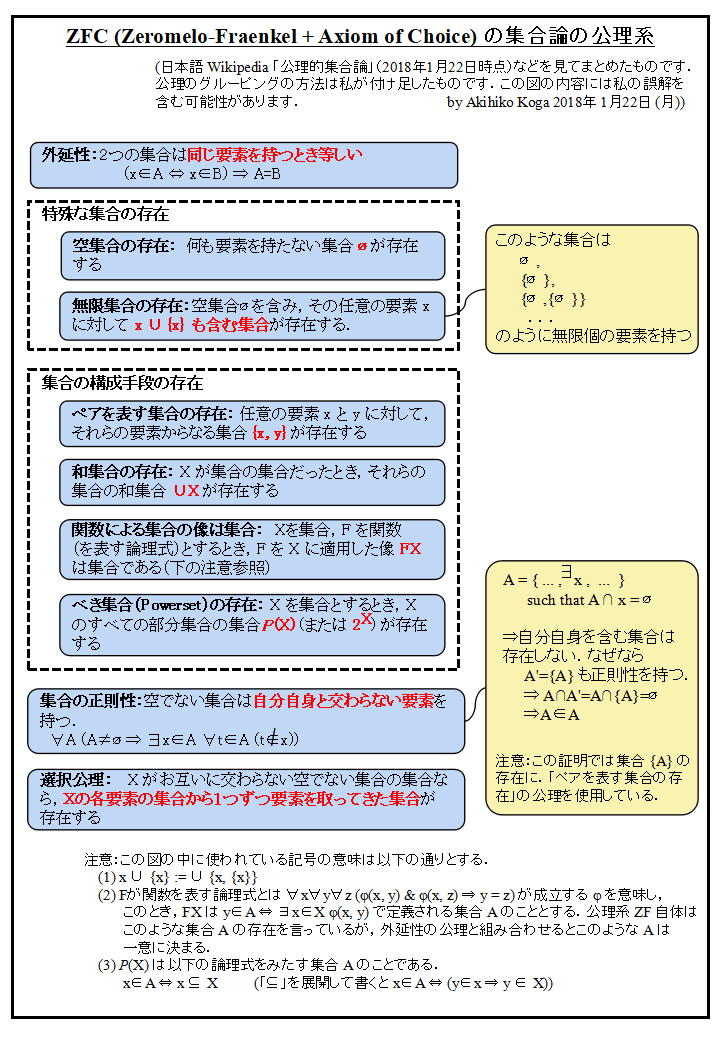
図のまとめ方は私が感じたまとめ方になっていますが,ZFC の公理系は5種類
の公理(群)からなっています.まず,第1に,集合が等しいとはどういうことかを決める外延性公理,第2に特殊な形の集合の存在(つまり空集合と最低限1つの無限集合),
第3に既存の集合から新たに集合をつくる手段の提供(ペア,和集合,関数適用,べき集合),
第4に自分自身を含むような集合の排除(ラッセルのパラドックスなどの排除)のための
上で書いた新たに集合を作る手段の関数適用のところは,
集合への関数適用の結果は集合になるという公理ですが,もとはここには分出公理(集合の中からある性質を持つ要素だけを取り出したものは集合)があったが,1922年に Fraenkel によって上に書いた公理に置き換えられたとのことです.分出公理は現在の公理系から導くことができます.
しつこいかもしれませんが,さらに ZFC の公理系の全貌を簡単にまとめた図を描いておきます. 本当は上の図でも描こうと思ったのですが,描いているうちに大きくなりすぎてポイントがぼやけて しまったので,もう一枚の図で補足しておきます.ポイントは,
- 考察する世界(ユニバース=集合の集まり)を構成するのに,まず集合のタネとして 空集合と最低1つの無限集合を仮定すること
- すでにある集合から新たに集合を作る手段として4つの方法を用意すること
- こうしてできた集合の性質として,外延性,正則性,選択関数の存在を課すこと
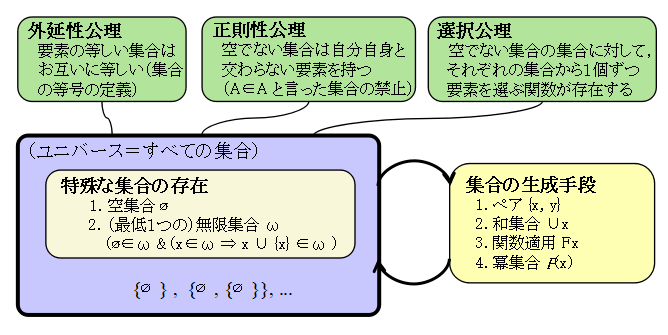
実は選択公理も集合を作るので,「集合の生成手段」に入れても良いかもしれません. ただ,「選択公理を仮定すれば...」というように,ほかのZF の公理系との結びつきは多少弱いように思うので,この図では別のところに書いています.
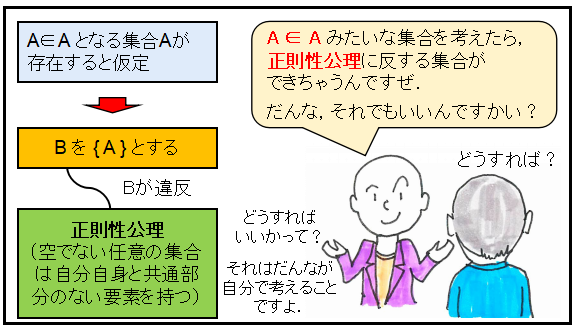
ところで,ここでの集合の公理の中で,私は,どうしても
に,そのことについて書いてみました.もし,私と同じように(かどうか分かりませんが)
渕野昌 : Is "naive set theory" really that naïve?, 数理解析研究所講究録 (2012), 1787: 183-189
タイトルがとても面白いと思います.普段,私たちはあまり意識せずに naïve set theory と言って おり,この言葉を使うたびに頭に浮かぶ「いったいこの言葉は正確には何を指すのだろう?」という疑問を黙らせて過ごしているように思います.このことについてきちんと考察した論文であり,貴重だと思います.
Tom Leinster: Rethinking set theory, 2012, pp1-8
この文献は arXiv
Rethinking set theory
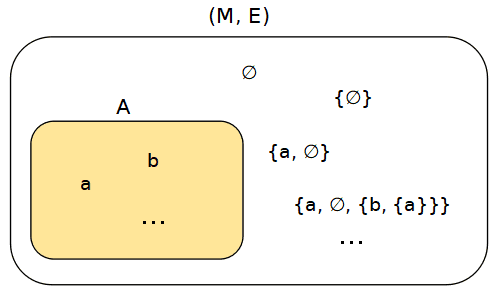
にあります. 圏ベースの集合論はなんとなく抽象的な感じがして敬遠していたのですが, この論文を読んでみたところ,むしろこの主張の方々は,直観にあう基礎を作りたがっているの かもと思うようになりました.およそ次の図のようなことが書いてあります.
でも,個人的にはZFCで円周率πが集合であってもあまり違和感はないです. 無理数を切断で定義するやりかたとかは,数を2つの集合のペアと思っているわけですから. 慣れというか,感覚の麻痺の問題じゃないでしょうか.あと,上の表で f : X → Y から f-1(y)をとる操作の存在の要請は,どこに分類したらよいのかはっきり理解していません.最後の選択公理にも関係しているような気もしますし.すみませんが,興味のある人は自分で読んで,ご判断ください.
ちなみに,この論文に関しては
Asaf Karagila : On Leinster’s “Rethinking set theory
で議論が戦わされています.本人(Leinster) も後で参戦されていますが,Asaf Karagila という人が,あまり圏論的な集合論を好きになれないということで,自分の ブログを持ったのを機会に意見表明されたみたいです.かなり濃く長い議論が交わされていて 面白そうなのですが,私は英語読むのが大変だし,英語じゃなくても議論そものもが 大変そうだしで,根をつめて読んではいません.また時間ができたら読ませてもらおうかと 思っています.皆さんもご興味があれば見てみると面白いかもしれません.Tom Leinstr: Basic Category Theory. 2014 の第3章 Interlude on sets
「集合に関する幕間」ですかね?
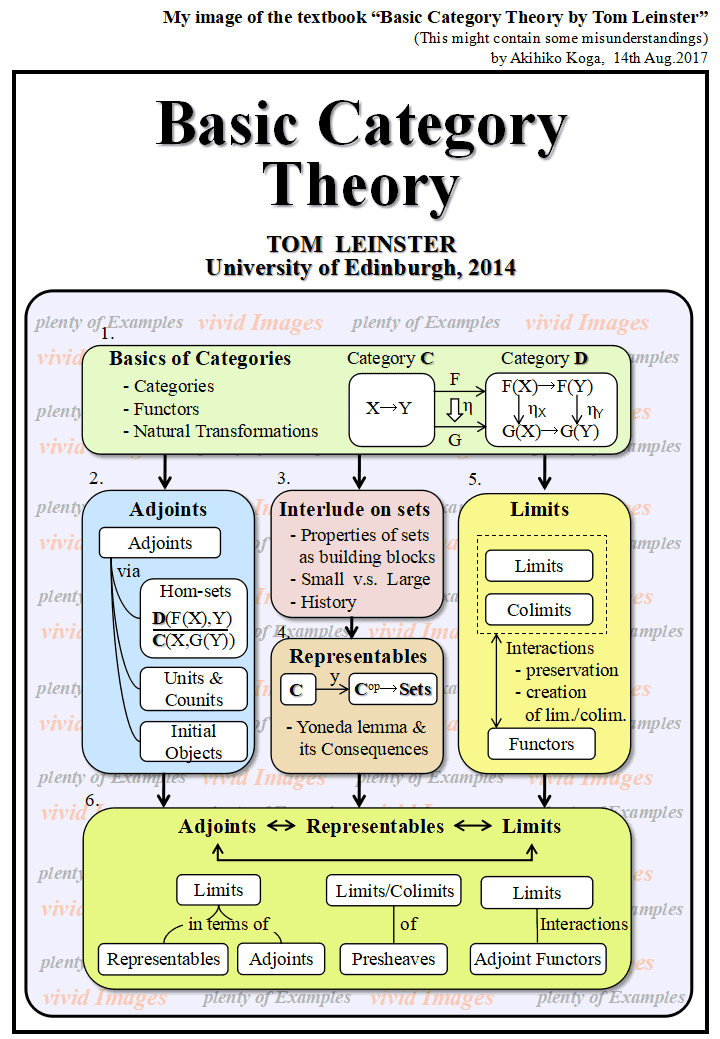
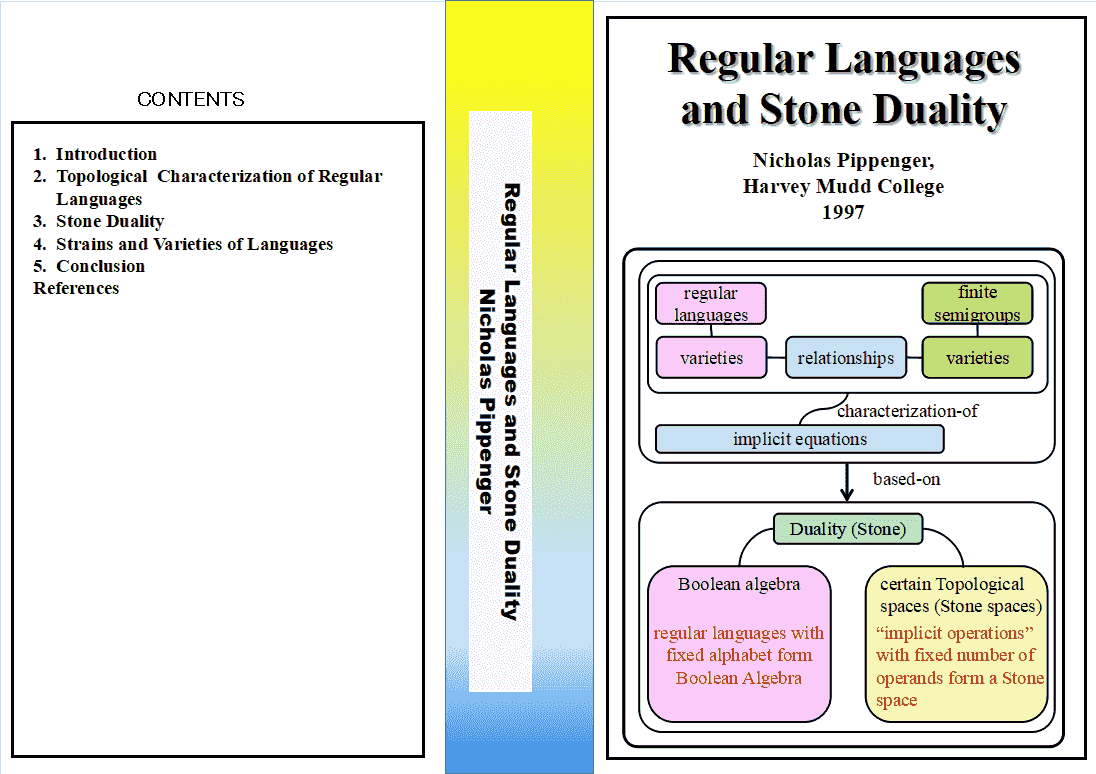
上の論文とかなり似ています.実は,上の論文を読んで間もなく, その論文がLeinsterだと忘れていて,この章を読んでところ 「あれ? どこかで読んだ内容だな」と思ってしまいました. こちらは圏論の教科書で次の章の Representables (米田のレンマ, 集合を"利用した"圏の表現)のために 集合について一言言っておくという内容です.ただ,こちらは, 圏による集合の特徴づけのほかに, 集合になる小さな圏,集合にならない大きな圏の話, また,集合論についての歴史的な話もあります. どちらにしても,これできちんと集合論について勉強するための ものではなく,ちょっとした読み物という感じです.18ページしかないので, ざっと読んでおくと,ほかの読みものを読むとき役に立つと思います. 本全体の構成と第3章の「幕間」の関係は次のような感じです.
こちらは 上の絵の下絵です.手書きで,ちょっと汚いですが,日本語なので残しておきます.
ここでも標準的な ZFC (Zermelo-Fraenkel + Axiom of Choice) の拡張として
クラスを許す von Neumann-Bernays-Gödel の集合論, Morse-Kelley の集合論 を
述べましたが,他にも,
代替的な集合論の積読(To Read List)に積読リストを作っておきました.
某勉強会で発表した「代替集合論」の発表資料