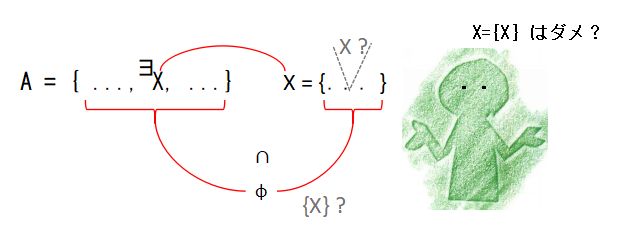
∀ A (A ≠ ∅ => ∃ X ∈ A (X ∩ A = ∅))
(空でない集合は自分自身とまじわりの無い要素を1つは持つ)
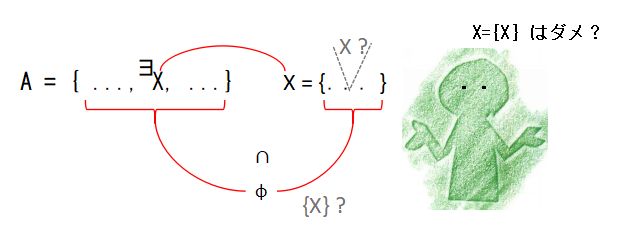
本当は,
というように脅かされている気がして気分が悪い.これは公理の形こそ肯定的な文章になっているが,私には背理法の匂い注)がする.もし,A ∈ A となる集合や Ai ∋ Ai+1 となる集合の無限列があったらこの正則性の公理に反する集合を簡単につくれちゃいますぜ.それでもいいんですかい?
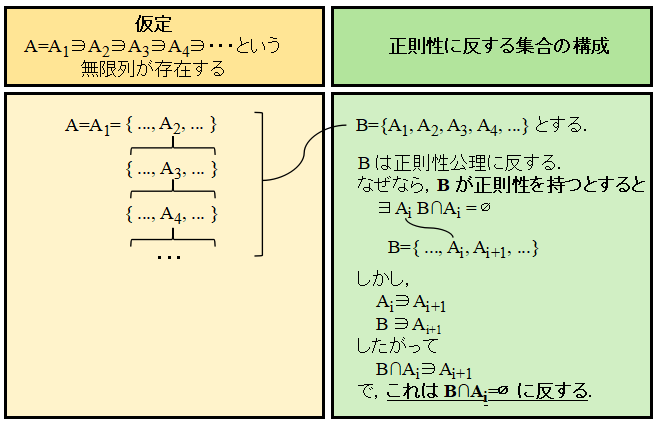
次の図のように,このような無限列 A1 ∋ A2 ∋ A3 ... が存在すれば
とすることにより正則性に違反する集合 B を作れる.こういう大元の集合の A が違反すると言わずに,わざわざ B を作って,それが違反するというところがいやらしい.B := {A1, A2, A3, ...}
これは,A ∈ A のように書くとすぐには見て取れないが,A ∋ A とかくと,
という無限列ができるから,上の場合の特殊な場合になっていることが分かる.A ∋ A ∋ A ∋ A ∋ A ∋ A ∋ A ∋ A ∋ A ∋ ...
でも,単独でも証明しておこう.
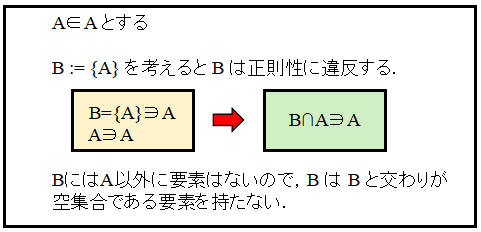
A を A ∈ A となる集合とする. 次の図(と言って良いかどうか)のように B := {A} とおけば,この B が正則性に反する.
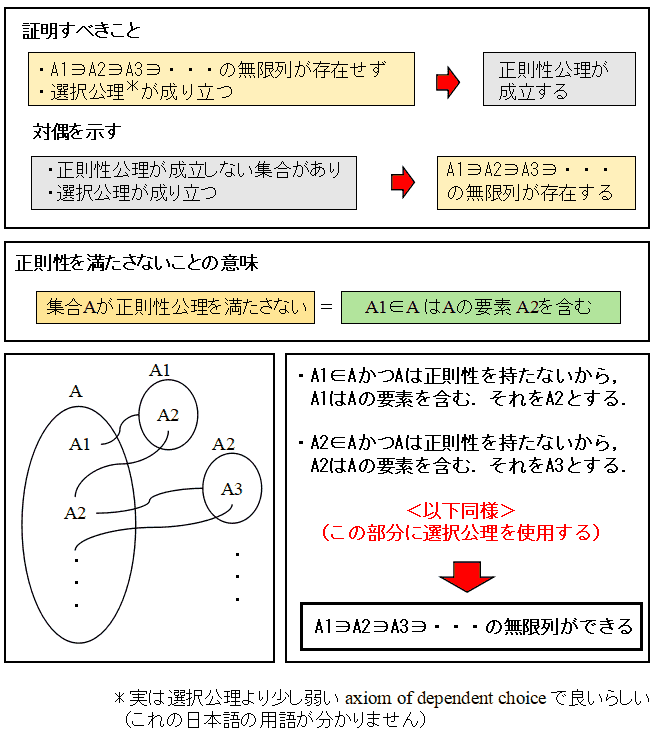
対偶をとり,選択公理が成り立つとの仮定の下に,正則性を満たさない集合があったとき,正則性を満たさない集合があったとき,A1 ∋ A2 ∋ A3 ...という無限列が作れることを示します.
正則性を満たさない集合 A があったとすると,A の任意の要素 X は A の要素を含みます( つまり ∀X (A∋X => ∃Y (X∋Y & A∋Y)).ですから, A の勝手な要素 A1 をとると,A1には A の要素がありますから,それを A2 として, A2 は A の要素 A3 を含みますから,A3 を取ってと言う具合に,次々に ∋ 関係にある集合の列
A1 ∋ A2 ∋ A3 ...が得られるわけです.ただし,ここで無限回の要素の選択が必要ですから,選択公理を使う必要性があることに注意してください.
私が正則性の公理に感じる気持ち悪さは,その意図は
どんな集合の要素を ∋ 関係で辿って行っても無限列は作れないのはずなのに,
〇〇な要素が存在するという形の公理になっていることなんです.それじゃあ,「その存在する以外の要素に ついてはどうなるのだろう?」という疑問が湧いてきます.それなのに, すべての集合について,その要素に ∋ の無限降下列を禁止できていると!
A を集合としたとき,その要素すべてについて A との共通集合が空である必要は ないのだから,そのようなお目こぼしにあずかった要素をつないで,∋ の 無限列を作れないのだろうか? いや,これは上の
で証明したのだから無理なんだろうけど,「なんで?」.たぶん,と言うか,上の 証明から,こういう ∋ の無限列ができるような状況が生じたときは, うまく集合を構成しなおして,つまり余分な部分を削り取って,正則性に 違反する集合を作れるということがミソだと思うんだけど.正則性 => A ∋ A1 ∋ A2 ∋ A3 ... という無限列は存在しない
正則性に違反する集合の再構成をもう少しみておきましょう.
それぞれの集合について,その要素との共通集合は,
A ∩ B = {B} ∩ {A} = ∅だから A も B も直接は正則性公理に違反しないけど,この二つで ∋ が 巡回する集合集合を作ることができる.A ∋ B ∋ A ∋ B ∋ ・・・ですね.
B ∩ A = ∅
これから正則性を持たない集合は C := {A, B} とやればよい.うーん, 証明のままですね.連立方程式を行列を使って1つの1次式にしている ようなものかな.
上に書いた最後の
の証明からは,正則性の公理の正体は,∋ の無限降下列の禁止を 選択公理と独立にしたものみたいですね.A1 ∋ A2 ∋ A3 ... という無限列は存在しない & 選択公理 => 正則性
別のところでも書いたが,公理的集合論 ZFC 以外の いろいろな集合論(alternative set theories),たとえば,ここの正則性公理が成り立たない集合論など, を調べる機会があった.それで分かったのだが,この正則性の公理( 基礎の公理 axiom of foundation とも言う)は成り立ちからしてちょっと技巧的な 感じがする公理のようだ.
この公理は,フォン・ノイマンの提案により,1925 年に ZFC に追加された.
フォン・ノイマンは
といった集合を次々に作っていってそれを順序を表すために使うというものである.こうして作った任意の二つのフォン・ノイマン順序数 X, Y は X∈Y または X=Y または Y∈X のどれかになっている.
話を元に戻して,正則性公理の意図としては,∈ の無限降下列が存在しないことの要請なのだが, フォン・ノイマン順序数だけの集合 x に対しては,この元の集合 x と交わりを 持たない要素 y∈x の存在は大変ありがたい.これは ∈ を順序 < と したときの x の最小値 min x になるからだ.つまり,
y1 < y2 iff y1 ∈ y2と定義すると,フォン・ノイマン順序数のある集合 x に対しては,
∃ y∈x (x ∩ y = ∅)という条件は,y に対しては,
¬ (∃ y1∈x y1∈y)となる.これは順序集合の最小値が必要な時,すぐそれを取り出すことができる 論拠を公理として与えることができることを意味する.
(つまり ¬ (∃ y1∈x y1<y) となり,y が x の中の最小値)
正則性公理は,集合の要素として,それ以上要素を持たない「もの」として∅以外に 許すとき(そのような「もの」をアトム(atom)と言ったり,Urelementというが),
∃ y∈x (x ∩ y = ∅)の形では言うことができない.例えば,a をアトムとして,「もの」
aの中には要素がないので,上のような y∈a の存在は言えない.小さいことを 言うようだが,
set(x) → ∃ y∈x (x ∩ y = ∅)のように x が集合ならという条件 set(x) を付けることになる.また,その時の y は当然 x の 中の要素の最小値ということではなくなる.それは例えば,もうひとつアトム b をとって,x={a, b} としてみればよい. a と b の間に ∈ 関係はないのであるから,どちらが最小ということもない.ということで,正則性公理の上の形は, ZFC のようにすべてが ∅ に還元される集合論とフォン・ノイマン順序数を順序の 基準に取っているとき役に立つことになる.
基礎の公理/正則公理の表現方法としては,もう少し素直に,∈の無限降下列が 存在しないという表現方法もあるようだ.ただし,無限降下列の定義も難しいので フォン・ノイマンのこの形の正則性公理は便利かつコンパクトな表現であるということは 言えると思う.
集合,位相,論理などへ戻る