形式的論理体系の定義から

レーベンハイム・スコーレムの定理までの大急ぎのまとめ

(Rapid Summary from Syntax of Logic to Löwenheim-Skolem Theorem)

by Akihiko Koga
27th Mar. 2020 (Update)
13th July 2018 (First)

集合，位相，論理など へ
ホームページトップへ戻る

目次

概要

某勉強会で今年(2018年)の10月に連続体仮説(の否定)を解説すると宣言してしまった． 自然数の集合 N と実数の集合 R の間に中間的な大きさの集合を挟んでも ZFC集合論に矛盾しないということの 証明に関する解説である．

その解説の中でレーベンハイム・スコーレムの定理（Löwenheim-Skolem Theorem）を 非常に手短に説明しなければならないので，ここで少しずつ書きながら， 本番の資料を改良していこうと思う．なお，その勉強会の顛末とその時の資料の表紙に ついては 某勉強会での連続体仮説の解説についての顛末に書いた(2019.04.25 追記)．

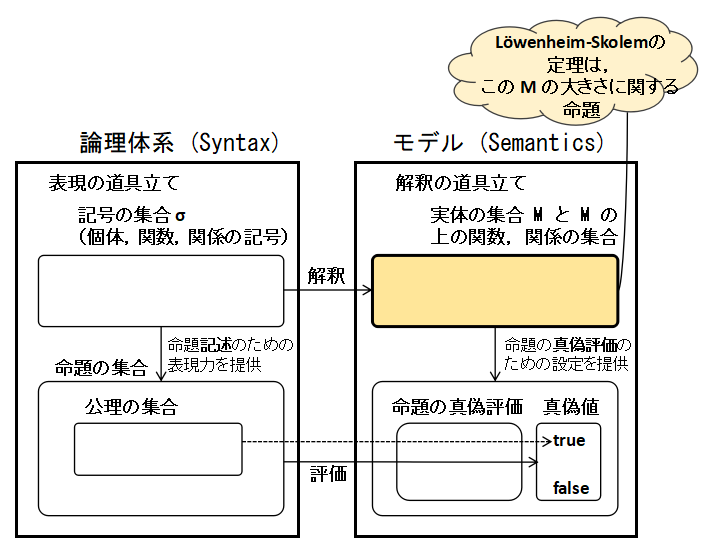
レーベンハイム・スコーレムの定理（レーベンハイム発表 1915年，スコーレムによる厳密な証明 1920年）は，一階の記号論理体系（一階述語論理）の「モデル（その体系の公理系を 満たす数学的な実例）」のサイズに関する定理である．後でもう少し詳しく説明するが，前提と なる枠組み，つまり，記号論理の体系やモデルなどの概念についてちょっと説明しておく．

１９世紀の終わりから２０世紀にかけて，数学の 世界では，数学的な推論過程の正しさを確信するために，それ自身を数学的対象として研究 する必要に駆られていた．その枠組みが下記のようなものである．図の左側は，数学での言葉と 推論過程の枠組みで Syntax の世界と言われる．ここでは，数学で使う表現の道具立て（ 定数，関数，述語などの記号）を用意し，その上に色々な命題を書けるようにする．それらの 命題の一部分を公理として，それからある規則を適用し「正しい」命題を導出していくのが 数学の推論であるとするのである．

この Syntax の世界は記号とその操作の世界である．それに対して，図の右側は， その記号が表す実体と操作の意味を定める世界で Semantics の世界と呼ばれている． 左側の Syntax の世界で提供された記号を解釈するための集合 M を与え，左の 記号の実際の値を決め，左の命題の真偽を評価する枠組みを与える．この枠組みの左で 公理に選んだ命題がすべて成立するものを左の体系の「モデル」という． 例えば，算術の体系の場合，左側では 0 とか 1 とか + とかの記号が提供され， 1+(1+1) などの式が記述できるようになる．右では，自然数の集合が提供され，記号の 0 を自然数の 0 で 解釈したり，式の 1+(1+1) を 3 と評価したりといったことができるようになる． 「論理体系がモデルを持つ」という性質は，「少なくともそのモデルは矛盾を起こさない」ことを 保証することであり，とても重要な性質である．

レーベンハイム・スコーレムの定理は，このときの記号を解釈するための「実体の集合 M」の 大きさに関する命題である．より詳しく言うと， 記号論理の体系がモデルを持つと 分かったとき，そのモデルを非常に巨大な大きさにしたり，またはその逆に， 非常に小さくしたりできると いう定理である．

上でも述べたように，記号論理のある公理の集合Ａがモデルを持つ，つまり，その公理集合を満たす数学的な実例が あるということは，その公理集合が無矛盾であるとみなせることを意味する．

レーベンハイム・スコーレムの定理でモデルを 小さくするときは，自然数の集合のサイズ（可算無限 ℵ0）まで小さくできる．

我々は，自然数の集合サイズの集合については 直観もけっこう働くし，また，ノウハウも 溜まっている．したがって， ある公理系Ａにモデルがあるときは レーベンハイム・スコーレムの定理で 自然数の集合レベルのサイズのモデルまで 小さくして，扱いやすくして， 加工することで別の公理系Ａ’のモデルを 作るということができる． １０月の勉強会での連続体仮説の独立性証明も この方法を使う予定である．

ということで，（私が）レーベンハイム・スコーレムの定理を手短に説明しなければ ならないという動機が出てきたのである．

上で非常に簡単に述べたように，この定理を説明しようと思うと，一階の記号論理の体系（の Syntax）とモデルの説明をしなければならない．ここでは，次の３つ

を大急ぎで，分かった気になり，かつ，その後の連続体仮説の説明で使える程度には 正確に説明するのが目的である．

記号論理の文法 (Syntax) と意味 (Semantics)

まず，記号論理の体系とそのモデルについて説明する．

いきなり細部の定義からはじめると分からなくなりそうなので，概要を話して， 次に詳細なイメージについて記述する．

記号論理とモデルの説明（概要編）

もともと，これは，１９世紀の終わりから２０世紀の初めにかけて，集合論が 現れ，カントールのパラドックス，ラッセルのパラドックスなど数々のパラドックスが 発見され，人々が自分たちのロジックに疑いを持ち始めたことから始まる． つまり，それらのパラドックスが集合論のせいなのか，もしかしたら， そもそも我々の数学的推論自身に欠陥があるものなのか自信がなくなってきた のである．

ということで，記号論理学のそのころの目的の一つとして，数学で我々が行っている 数学的推論をきちんと書き出し，それが正しいことを証明することだった．

その枠組みが次の図（冒頭の Syntax & Semantics の絵をもう少し詳細に書いたもの）のようなものである．

図の左側（Syntax と書かれている側）が， 我々の数学的推論を記述しようとする体系である．ここでは下半分の 「数学的推論のメカニズム」というところに書かれているように，まず， 公理の集合を定めて，三段論法などの数学的推論を何段階か続けて，定理に 至るという我々が数学で通常行っているプロセスを記述したいという欲求がある． このための前提として 左上の方に書かれているような，ものや関数の記号，関係を表す記号などを 定め，0 とか 0+1 とか 空集合 ∅ などの数学的対象の記述，また，それを使った 0+1 ≤ 0 などの命題を記述する仕掛けを作る．この道具立てとして導入した関数記号や 述語記号の集合をシグニチャと呼ぶ．ここではσというシグニチャが導入されたとする． 公理や定理はシグニチャσが与えられたとき，その上に作られた 命題の集合の部分集合になる．

こうして命題の集合が厳密に定められ，そのうちのいくつかが公理として設定され，そこから あらかじめ決められた推論ルールを何度も適用しながら，定理となるべき 命題を証明していく．

こういう我々が数学で行っているらしいプロセスを記述する ことはできたが，今度はこれが真理にたどり着く正しい方法だろうかという判断方法が 必要になってくる．それを判断するのが，図右側の部分（Semantics と書かれた部分）である．

左側で命題と言っているものは，あくまで，単に文字列である．推論規則は文字列の 集合から新たな文字列を作り出す規則である．例えば，1+1+0 と書いてあれば，これは イチ，プラス，イチ，プラス，ゼロという文字列であって，2 を表しているという 意味付けはここではまだ無い．もちろん，公理系をうまく選んでやれば， 0+1+1=1+0+1, 1+0+1=1+1+0, 1+1+0=2 などの等式はこの記号論理の体系で証明できる だろう．しかし，これはこの記号論理の中のいくつかの記号列がお互いに等号で結ばれる 関係になっているということを表すに過ぎず，これが我々の意図と同じということは 言えない．したがって，我々がこの記号論理の体系に込めた意図を表す仕掛けが 必要になって来る．図の右側の仕掛けはそのために左側の文字列に数学的な意味を 与えるためのものである．

右側の一番基本的な部分はσ-構造と書かれている部分である．これは 左側で導入されたシグニチャσを解釈する構造である．まず， ここでは左側の体系で扱う「もの」の集合をさだめた集合 M を決める．そして，左側の 体系で現れる関数記号や関係記号を，M の上の関数や M の上の関係に対応付ける 関数 m を定める．こうすると，左側の命題，例えば， 0+1 > 0 は右側で意味を持ってくる． 例えば，ものの集合として自然数の集合 N をとり， 文字 0 と 1 を数 0 と 1 に対応させ，文字 > を自然数 N の上の大小関係の 比較関係 > に対応させると，文字列 0+1 > 0 は真か偽か具体的に計算することが できるようになる．こういう与えられた記号論理の語彙 σ に現れる記号を解釈する 道具立てである集合 M と集合 M 上の関数の集合，関係の集合 をσ-構造 という．σ-構造と記号の集合σから σ-構造への対応 m が決まると，左の命題が 解釈できるようになる．このσ-構造と対応を合わせて，もとの記号論理の解釈という． さらに解釈のうち，左の記号論理で設けられた公理をすべて満たすものを， 与えられた記号論理の公理系のモデルという．

大急ぎで概念説明を進めてきたので，未消化だったり，疑問を持たれる方も多いと 思う．例えば，私は最初にこの定式化を勉強した時，次のような疑問を持った．

そもそも，我々の数学的推論のプロセスが正しいかどうかを検証するために このような記号論理の体系を作ったのではないか？　では，右側のモデルに 翻訳された個々の命題の真偽はどのようにして判断するのか？ これは，もしかしたら，間違っているかもしれないと疑っている， 普通の数学的推論で判定するのではないか？　これは本当に我々の 数学的推論の検証になっているのか？　議論がサイクルになっているのでは ないか？

結論から言うと右側での命題の正しさの判定は普通の数学的推論で行う．「十分注意しながら」 という但し書きが付くとは思うが．

この状況をある人はサイクルでないという．私はサイクルだと思う．ただし， 「十分注意しながら」だし，一度，我々の推論がどんなものがきちんと書き下して あるので，このサイクルも意味のあるサイクルなのじゃないかなと感じている．

サイクルかそうでないのかを議論しはじめると，たぶん，サイクルとはなにか， どうなればサイクルなしで説明したことになるのか，など実りの多い議論になるとは 思うが，私は疲れるので，上の，「一度数学的推論」を机の上において眺めたという 実績を評価して，この枠組みを使わせてもらうことにしている．

記号論理とモデルの説明（詳細編）

前節で，記号論理とそのモデルのおよそのところは話した．ここでは，このページの 本題であるレーベンハイム・スコーレムの定理を説明できる程度に 記号論理とモデルの詳細に入る．

レーベンハイム・スコーレムの定理はモデルの 大きさに言及する定理である．したがって，記号論理で指定できる「もの」がどれだけ 多いかということを無視しては成り立たない定理である．ここでは，主に，この部分， つまり，どのような記号とそれらの組み合わせで記号論理の中の命題ができているかを 中心に上での説明を詳細化して話す．

いままで左の世界を記号論理の体系と呼んでいた．また，時々，「一階の」記号論理と いうように「一階の」という修飾子を付けたりしていた．多少，用語が乱れているが， これから話す体系は「一階述語論理」と呼ばれているもので，かつ， 「ヒルベルト流」の 体系を念頭に置いて話す．

「一階」というのは，命題中に，「任意の（∀）」とか 「存在する（∃）」の限量子と呼ばれるものが，関数や述語（関係）には 掛からないという意味である．逆に関数や述語に掛かる場合は，「二階」の体系と 呼ばれる．一階であることは，レーベンハイム・スコーレムの定理に本質的である． レーベンハイム・スコーレムの定理は一階の述語論理で成り立つ定理である．

こういう記号論理の体系には，大きくヒルベルト流 (Hilbert-style) と， もう一つゲンツェン流 (Gentzen-style) がある (たとえば，NK や LK)． 主な違いは，公理の量と数学的推論規則の量のバランスである．ヒルベルト流は 公理をたくさん入れて，推論規則を極端に少なくとる． 通常，モーダス・ポーネンス（三段論法 modus ponens, A と (A → B) から B を導く）と全称化（A(x) から ∀x.A(x) を導く）の２つだけで， 全称化を公理の中に押し込めて，モーダスポーネンスだけでやるものもある． とにかく，推論規則が単純なのである．これに対して，ゲンツェン流では 推論規則は２０個程度あり，我々の通常の推論規則に近い．

では，次の図を使って一階述語論理の体系とそのモデルについて説明する．

シンタクスの世界の説明

まず，左のシンタクスの世界から説明する．命題を記述するための基盤となる記号の集合 σ は 関数記号の集合と関係記号の集合の２つからなる．関係記号は述語記号とも言われる． モデルの大きさがどのくらいになるかは，σ に含まれる記号の多さに依存する．

関数記号も関係記号もそれがいくつの引数を取るかが予め決められているとする．通常， この数を関数記号の arity ，関係記号の arity という．arity は 0 でも良い．arity 0 の関数記号は引数を取らないである値を返す関数を表すので，これは定数と同一視される． 図の中で関数記号の中に点線で囲われた部分がそれを表している．

シンタクス側のもう一つの道具立ては，その下に書かれている変数記号の集合である．この 意図としては，命題の中で色々な元を取り得るものを表す．以下の記述では， 変数記号の集合は常に可算無限個であるとしておく．

関数記号の集合と変数記号の集合が決まると，「もの」を指し示す 「項（terms）」を 定義することができる．これは次のような方法で関数記号や変数を組み合わせた文字列である．

  1. 変数記号は項である
  2. t1, ..., tn が項で，f が arity n の関数記号のとき，f(t1, ..., tn) は項である
    ただし，f が arity 0 の関数記号のときは，f 単独でも項である．
  3. この２つの規則で作られたものだけが項である

「もの」を指し示す「項」の概念が定義出来たら，次は，それらの項がある関係にあるという 言明を定義することができる．つまり，t1, ..., tn を項とし，P を arity n の 関係記号とするとき，

P(t1, ..., tn)

を原子式（atomic formula）という．これは，項 t1, ..., tn で 指し示されている「もの」が P の関係にあることを意図した式である．こうやって， 言明の一番基本が定義出来たので，次は一般的な言明 「論理式（formulas）」が定義できる．これも項と同様，次のように 再帰的に定義される．

  1. 原子式 P(t1, ..., tn) は論理式である．
  2. αとβが論理式であり，x が変数記号であるとき，
    1. α ∨ β は論理式である．
    2. ¬α は論理式である．
    3. ∀x.α は論理式である．
  3. この２つの規則で作られたものだけが論理式である

さらに，α ∧ β は ¬(α ∨ β) の略，α → β は， ¬α ∨ β の略， ∃x.α は ¬(∀x.(¬α)) の略であるとしておく．

また，論理式に現れる変数についての用語として束縛変数，自由変数という用語を 定義しておく．論理式 ∀x.P や ∃x.P において，P の中で x は 束縛されているという．束縛されていない変数を 自由であるという．束縛されている変数を束縛変数， 自由な変数を自由変数という．

以上で，一般的な言明を記述するための論理式を定義することができたので， つぎは，これを推論していく機構を定義する．

まず，公理という用語から定義する．その体系で選ばれた論理式を公理という． 公理は有限個でも無限個でも構わない．ただし，どんな体系を作るにしても，論理的体系を 成立させるために，最初から選ばれている公理がある．例えば，P→P などである． これについては列挙するのは煩雑になるので，ここで改めて列挙することはしない．Wikipedia など，適切な述語論理の文献を参照いただきたい．

シンタクス側の最後の道具立ては，推論ルールである．先に述べたように， ヒルベルト流の証明システムでは， この推論ルールを非常に少なるとるのが流儀みたいで，通常，次の２つが使われる．

以上で，シンタクスの世界の説明を終わる．沢山の用語がでてきたので，まとめを 付けておく．

シンタクスの世界のまとめ

セマンティクス（意味，semantics）の世界の説明

セマンティクスの世界は，上で定めたシンタクスの世界で作られた項を なにか「もの」に対応させ，論理式の真偽を解釈する機構である．

まず，シンタクスの世界で作られる項を解釈するための集合 M を定める．

次に，シンタクスの世界での関数記号 f の M の上の関数への対応 m(f) を決める．このとき，f のアリティが n なら，m(f) は 関数 Mn → M の関数を対応させる．n が 0 の時は m(f) は M0 → M の関数であり，それは M の要素と同一視する．

これにより，再帰的に項を表す M を決定することができる．例えば，g(a, f(b)) に対しては，

m(g(a, f(b))) = m(g)(m(a), m(f)(m(b))
となる．

述語記号 P については，M の上の関係 m(P) を割り当てる．つまり，m(P) ⊆ Mn である．

今述べた，M, m(f), m(P) がシンタクスの世界の解釈の基本になる．これをシグニチャーσの構造 という意味で，σ-構造（σ-structure）という．

σ-構造はが決まると，変数を含まない原子式の解釈ができるようになる．つまり， t1, ..., tn の項に変数が含まれないとき， P(t1, ..., tn) の 解釈を次のように定める．

P(t1, ..., tn) が成立する ≡ (m(t1), ..., m(tn)) ∈ m(P)

これらをもとに自由変数を含まない論理式，つまり閉論理式 P に対しては次のように再帰的に真偽を決めていく．

以上で，閉論理式については，真偽が定められた．問題は，自由変数を含む論理式であるが， これは，

その自由変数が M のどんな要素をとっても成立するとき，その論理式を真とし， それ以外の場合は偽とする
と言う方法で真偽を定める．要は，それらの自由変数には ∀ が掛かっているのと 同じである．

以上でシンタクスの世界で作られた論理式の解釈の方法を述べた．

次にシンタクスの世界で独自の公理が与えられている場合（論理として成立させるための 予め組み込まれている公理以外の公理）であるが，ここで与えた集合 M への解釈 m がそれらの 公理をすべて満たす時には，M あるいは m も含めて，そのシンタクスの世界の体系の モデルであるという．

以上で，シンタクスの世界を解釈するセマンティクスの世界の機構について説明し終わった． こちらも導入した概念のまとめを作っておく．

セマンティクスの世界のまとめ

レーベンハイム・スコーレムの定理と集合論での解釈

ここでは，「ダウンワード・レーベンハイム・スコーレムの定理」 （あるいは可算レーベンハイム・スコーレムの定理）と呼ばれるものを説明する． 定理の内容は次の通りである．

可算(または，ダウンワード・）レーベンハイム・スコーレムの定理
(Countable Löwenheim-Skolen Theorem)

シグニチャー σ が可算無限個の一階述語論理が，無限基数のモデルを持てば， 可算無限の基数のモデルも持つ．

ただし，変数記号の集合は可算無限個であるとする．

レーベンハイム・スコーレムの定理としては，もう一つ，アップワード・レーベンハイム・スコーレムの定理というものがあり，こちらはσの基数以上ならとんな基数 k のモデルも存在すると いうものである．

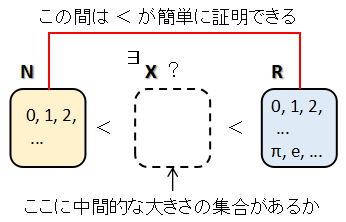
まず，定理の文章だけでは何を主張しているのか掴みにくいので，一番最初の単純な図に 戻って，この定理の言っていることを解釈してみよう．

つまり記号の集合σが可算無限個の述語論理がモデルを持てば，図右側に おける，その述語論理での項を解釈する集合 M も 可算無限個（基数 ℵ0）で済むということを意味する．

レーベンハイム・スコーレムの定理は，それが発表された当時（1915年, 1920年）は， レーベンハイム・スコーレムのパラドクスと言われていた． これは，この定理の集合論における解釈がパラドクスのように見えるからである．

いま，記述しようとしている体系が集合論で，ZFC のような体系で記述されているとする． シグニチャは論理記号の = と ∈ だけである（記述を見やすくするために ∅ など， 「もの」を表す記号を加えても良いが，無くてもよい）．このとき，右側の M は，ZFC の 理論体系で作られ得るすべての集合を含んだ集合である．レーベンハイム・スコーレムの定理は， この M が可算集合で十分であるというのである．

この帰結は，少し加工すると，

集合論 ZFC のモデルとして，すべての無限集合が可算集合であるモデルが存在する
という形にできる．一方，左側の ZFC の公理からは，依然として，
集合 X から，すべての部分集合の集合 P(X) へは全単射は存在しない
（|X| < |P(X)|）．

従って，非可算集合 P(ω) が存在する（ωはすべての自然数の集合）．

が証明できる．つまり，ZFC で定めた公理系からは非可算集合の存在が証明できて，一方， それを解釈するモデルとしては可算集合だけしかないモデルが存在するということである． 当初，これはパラドクスと捉えられていた．

しかし，これは次のような解釈で，パラドクスでは無いということが分かってきた． つまり，「冪集合P(X) はもとの集合 X より真に大きい」という命題は，実は，

P(X) から X へは単射 (injection) が存在しない
ということを言っているのである．例えば，モデル M に次の図のような単射 g を 加えなければ，そのような状況になる．つまり，可算集合が集まって，それらの集合の 間の関数をモデルに加えるか加えないかで，それぞれの集合の大きさを演じるような モデルを作ることができるという訳である．

もちろん，関数個別に好き勝手にモデルに追加する/しないを決められるわけではない． 例えば，f1 : X →Y, f2 : Y→Z がモデルに入っていたら，関数 f2・f1 : X→Z は モデルに入っている必要がある．こういう制約を守りつつも，全部が可算無限集合で， 非可算無限を演じることができると言っている訳である．

参考までに，連続体仮説の解説のとき作成したこの状況を表す絵をのせておく．

連続体仮説およびその否定の ZFC 集合論からの独立性証明は，それぞれが 成り立つ/成り立たないような ZFC 集合論のモデルを作ることによってなされる． これにはいろいろな証明方法があるようであるが，一つの方法として， レーベンハイム・スコーレムの定理で保証される可算モデルを使う方法がある． つまり，すべての無限集合が可算無限のモデルを持ってくれば，その間の単射として 何を加えるかで，それらの大小を決めることができる訳である．すべてが可算集合で あるから，原理的には中への単射は作りたい放題である．都合のよい単射を加えて， 連続体仮説が成立する/しないモデルを作ればよい．もちろん，そうして作ったモデルが 実際に ZFC の公理系を満たすことを確認しなければならない．ここらあたりの保証が フォーシング（forcing）と呼ばれる技法である．このページは， レーベンハイム・スコーレムの定理の解説なので，これ以上，ここでは連続体仮説には 深入りしない．

レーベンハイム・スコーレムの定理の証明

この定理は単独で証明してある本もあるし，また，完全性定理（Kurt Gödel 1929年）の系という扱いの本も ある．実際，完全性定理の証明は，その体系が無矛盾であるとき，シグニチャ σから生成される 項の集合にある同値律を入れて，その商空間として作成される．したがって，基数 |σ| の モデルが得られるわけである．ここでは，たった今述べた第二完全性定理との関係で証明される ということをもう少し詳しく書いておく．直接の証明は，もしかしたら，元気がでていつか書くかもしれないが，当面は書かないと思う．

完全性定理を使った証明のアウトライン

まず，完全性定理を書いておく．これは一階述語論理において，

証明できる命題＝すべてのモデルで正しい命題

を述べている定理である．

完全性定理（第１形）

φ を論理式とするとき，

|- φ ⇔ |= φ

つまり，φが証明できるための必要十分条件はφがすべてのモデルで成立することである．

この定理には同値な別の述べ方（第２形）がある．

完全性定理（第２形）

Σ を論理式の集合とするとき，

Σが無矛盾 ⇔ Σのモデルが存在する

つまり，Σから矛盾が証明されなければ，Σはモデルを持つ．また，逆にΣがモデルを 持てば，Σは無矛盾である（こちら側の含意はほぼ当たり前である）．

レーベンハイム・スコーレムの定理は，こちらの完全性定理の第２形と関係が深い．

第２形完全性定理の <= の含意はほぼ当たり前で，もし，矛盾が証明されるならば， モデルを持つことはできない．証明が難しいのは => の含意で，

その体系から矛盾が証明されないなら，その体系はモデルを持つ
という命題である．この証明には，与えられたシグニチャσと論理式の集合Σから， 具体的にそのモデルを作ることによってモデルの存在を示している．

次の図に完全性定理（第２形）とレーベンハイム・スコーレムの定理の関係を示す．

まず，前提として，シグニチャσは可算集合であるとする．シグニチャとは， その体系の項や述語を記述するための関数記号の集合と関係記号（述語記号）の集合 のことであった．関数記号には特に 0 引数の関数として定数記号も含まれる．

完全性定理（第２形）は赤く横長の四角で囲まれた部分であり，与えられた論理式の 集合Σが無矛盾ならΣのモデルが存在することを主張し，その逆にモデルがあれば Σは無矛盾であることも主張している．先にも述べたようにモデルがあれば無矛盾で ある（①）は自明である．難しいのは，Σが無矛盾であるときモデルがある（②）であるが， これは実際に，モデルを作成することにより証明される．それが③のラインである． ここで作るモデルは項モデルと呼ばれ，σの関数記号（含む定数記号）を組み合わせて，項の集合 Termσを 作成し，それを同値関係～Σ

t1 ～Σ t2 iff Σ |- t1 = t2

(つまりΣで t1 = t2 が証明できるとき，t1 と t2 は同値)

で商空間 Termσ/～Σ を取ったものである． 商空間 Termσ/～Σ は，項を作る元になった集合σが 可算集合であることから，可算集合になる． 実際は，この項モデルが∑のモデルになるためには，元のσと∑に次の条件が必要になる．

  1. ∑⊢∃φ(x) ならば，∑⊢φ(c)となるc がσの関数記号に存在す（c は witnessと呼ばれる）．
  2. ∑は完全，即ち，任意の論理式αに対して，∑⊢α または∑⊢￢α
ここでは証明を省くが，選択公理を仮定するともとのσと∑を拡張することにより， 基数を可算集合に保ったまま，これらの条件を満たすようにできる．したがって， まず，これらの条件を満たすようにし，その後で項モデルをつくれば，可算集合の モデルができる．

以上，論理式の集合Σにモデルがあれば，Σは無矛盾になり（①），Σが無矛盾なら Σはモデルを持つ（②）が，そのモデルは可算集合に取ることができる（③）． この①と③の２つを合成すれば，図の右側に縦に青色で囲んだ命題になり，これが丁度，レーベンハイム・スコーレムの定理である．

（補足）

（ダウンワード）レーベンハイム・スコーレムの定理成立の本質

当然のことながら証明は厳密にしなければならないのだが，レーベンハイム・スコーレムの 定理が成り立つ本質的な理由は，

有限，あるいは可算無限個の関数記号や述語記号から 作り出すことができる要素の総体は可算無限個である
ことによる．これは上の証明の中の Termσ/～Σ を 考えればわかる．

ちなみに我々の自然言語も有限のアルファベットあるいはかななどからなるので， それらの言葉で直接指し示すことができる数学的概念も，高々可算無限個である． 我々が直接言葉で表すことができるものは結構少ないのだ． 2019.01.17 (木)

二階述語論理などの関連事項

レーベンハイム・スコーレムの定理は一階述語論理で成立する定理である．二階以上では 成立しない（らしい）．二階述語論理とは，関数や述語に限量子（∀, ∃）を 使うことができる記号論理である．一階述語論理では対象の要素に対してだけ限量子を 使うことが許されている．

一階述語論理でレーベンハイム・スコーレムの定理が成立するということは，一階述語論理では 無限集合の実際の大きさを論理式で限定できないことを意味する．もし，これが出来たとしたら， 自由にモデルの大きさを可算無限から任意の無限基数に変えられないはずである．これは 自然数論に関して考えると奇妙な帰結を得る．我々は，自然数の集合 N は可算無限個の 要素からなっていると思っているが，ZFC のモデルの中には自然数の集合 N が非可算無限集合であるものも存在するということである．しかし，数学的帰納法は成り立つので，ある述語 P(n) がすべての自然数で成り立つためには，P(0) と P(n) → P(n+1) を証明しさえすればよい． 本来我々が自然数と思っている 0, 1, 2, ... 以外の非可算無限個の要素は 0, 1, 2, ... と同時に P(n) を成立させてしまう．

一階述語論理では，レーベンハイム・スコーレムの定理が成立して，このような奇妙な 現象が起こるので，もしかしたら，一階述語論理では我々の数学は記述できないのでは ないだろうかという気がしてくる．そうすると二階以上の論理に期待してしまうが， 世の中を見渡したところ，二階以上の記号論理はまだそれほど整備されていない．私は 二階以上の数理論理学に関して包括的に書いてある成書は知らない．どちらかというと， 論文をたくさん集めることによってはじめて，二階数理論理学の姿が見えてくると いった状況のように思う．

二階数理論理学について私が聞きかじった部分だけを書くと，次のようになる．

  1. シンタクスについては一階述語論理に関数と関係の値をとる関数の変数と関係の変数を 加え，それに対して限量子（∀, ∃）を付けることができるようにしたものが使われる．

  2. このシンタクスに対して２つの意味論が提案されている．
    1. standard semantics (full semantics)
    2. Henkin semantics

  3. Quine, Willard V によると，二階数理論理学は，「羊の皮を被った集合論」 らしい．つまり，一階述語論理で，集合論を定式化し，関数や関係を集合として 定式化してしまえば，一階述語論理の中でも関数や関係に限量子は使うことができるじゃないか という非難である．
    Willard van Orman Quine（1908年6月25日 - 2000年12月25日）は1930 年代に 新基礎集合論(New Foundation) を提案したアメリカの数学者/哲学者である． New Foundation では，すべての集合の集合が（クラスではなく）集合である 集合論 NF である．これが無矛盾であるかどうかはまだわかっていない．これを 多少修正した NFU と呼ばれる集合論は ZFC が無矛盾ならこちらも 無矛盾であるという相対的無矛盾性を持つことが証明されている．

以上のような理由もあって，私はまだ二階以上の論理学について真面目に勉強していない． ただ，いくつか読もうと思っている資料は集めたので，以下，それを列挙しておく．

二階数理論理学の勉強用の私の積読（つんどく）
検索すれば PDF が見つかります(Wikipedia 以外)．
  1. ETHAN JERZAK : "SECOND-ORDER LOGIC, OR: HOW I LEARNED TO STOP. WORRYING AND LOVE THE INCOMPLETENESS THEOREMS", 2009, pp1-22

  2. Marcus Rossberg : "First-Order Logic, Second-Order Logic, and Completeness", 2004, pp303-321

  3. J Väänänen : "Second order logic or set theory?", 2012, pp1-26

  4. Wikipedia の second-order logic

雑感

この定理をレーベンハイムが最初に発表したのが1915年であるから，これを書いて いる今（2018年9月29日），すでに 100年以上がたっている．この定理は， Gödel の完全性定理と非常に関係が深いのだが，完全性定理や不完全性定理ほど 有名ではないと思う．しかし，集合論における解釈はとても深遠である． なにしろ，言ってみれば，人間の思考は，可算無限の集合の世界で，それぞれの関係を 使って，可算無限でない集合があるように振舞っていれば，それを「本当の」 非可算無限と区別できないと言っているのである．

いま， 応用としての人工知能（AI）がもてはやされているが，時々は基礎に戻って， もうすこし，このような定理にも注意を向けて，人間の思考について再考することは 意味のあることではないだろうか．

参考文献

変更履歴
集合，位相，論理など へ

圏論を勉強しよう へ
束論を勉強しよう へ
半群論を勉強しよう へ
ホームページトップ(Top of My Homepage)