(about Zorn's Lemma and Axiom of Choice)
日記にも書いたが，ここしばらく選択公理からZornの補題 (ツォルンの補題) の証明を独力でやろうと
四苦八苦していて，先日（2018年7月26日（木））ようやく完了した．実は，はずかしいくらい
長い時間をかけた（日記には書いたが，こちらにはとても書けない）．色々考えたことも
あったので，ここではそういうことも含めながら，選択公理と Zorn の補題に
関すること（証明のアプローチ，証明の内容，応用，関連事項）を書こうと思う．ここで書く
話題は，どちらかと言うと，選択公理より
ここの内容は Zorn の補題を独力で選択公理から証明してみようと思う人にとっては
一種の
また，上に書いたように紆余曲折を書くつもりなので，ここの記事は
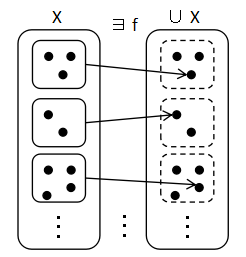
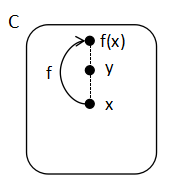
空集合でない集合の集合 X （つまり，x ∈ X ならば x は空でない集合)があり，かつ，X が空集合でないなら，X の各集合から１つずつ要素を選ぶ関数
f : X → ∪X で f(x) ∈ x for ∀ x ∈ X
が存在する．
選択公理にはいくつかバリエーションがあるが， ここではそのうちの一つを載せた．他に，X の集合がお互いに交わりがないとか， ∪ X = B として，X 側を P(B) = 2B にするなどの バリエーションなどがある．当たり前の内容に思えるが，無限個の選択でも保証する ところにポイントがある．
次は Zorn の補題を書いておく．Zorn の補題は，チェイン（全順序集合のこと．「鎖」 とも言う）の上が「上限」か「上界」の二つのバージョンが あるようだが，ここではより条件のきつい「上限」版の方を載せておく．結局はそれらは同値 なのだが．
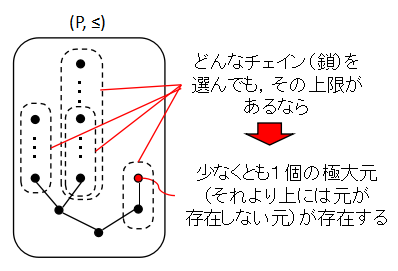
(P, ≤) を任意のチェイン（P の中の部分集合で全順序集合になるもの．鎖ともいう）に
必ず上限がある
順序集合とする．このとき， P には少なくとも一つの極大元（それより大きい元が存在しない元）がある．
（この補題の中の「上限」を「上界」に変えてもよい）
読み取りにくいかもしれないが，どの上昇列もどこかで止まっていたら， もう上に上がることができない元があるということである．これも 当たり前に見えるが，無限集合上の順序では威力を発揮する補題である．
選択公理と Zorn の補題は同値な命題として扱われるが，
選択公理 → Zornの補題 の証明
は逆よりかなり難しい．
実際，これらが同値なのは ZF の集合論の下にであって，
Zorn の補題 ← 選択公理 + 多くの ZF の公理と推論
となっているわけである．感覚的には次の図の左下側の配分位である （選択公理成分 : ZF 集合論成分 = 1 : 10 よりも ZF 集合論成分が多いかなと思う）．
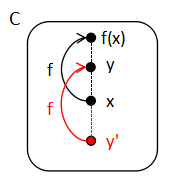
Zorn の補題の証明において，選択公理は，順序集合 (P, ≤) に，関数 f : P → P で，
f(x) = x if x が極大
> x otherwiseの存在を保証するだけである．そういう関数が存在すれば，ZF の集合論で，Zorn の 補題の残りの部分は証明できてしまう．つまり，
f(x) = x if x が極大
> x otherwise
が存在すれば，P には少なくとも１つの極大元がある．
が，ZF 集合論の中で言えてしまうのである．
ということで，まず，数学での用途だが，無限回の選択操作をやらなければ構成できないものの存在証明に使える．こちらは私の専門という訳ではないので，いくつかの例を挙げておくだけにする．
回転と平行移動でこれができるということは「スゴい」と思うが，我々は，
無限集合の場合，部分が全体と
書いていると長くなってきたので，「これは読むのが怠い」と思い，中断した．そのうち整理してどこかに書くが，ここでは書きかけたことの概要だけ書いておく（ということで，数学の方の 分量の方が多くなってしまった）．
もちろん，
その構成的な作り方は工夫を要するので，
Zorn の補題の証明方法は（私が知っているものは）次のような方針のものがある．
ここの考察や証明では，最初の，長いかもしれないチェインを構成することを考える．
インターネットで Zorn August Max lemma あたりで画像検索すると Zorn さんの顔写真がでてきます．あまり似てなくて申し訳ないですが，ご参考までに絵を描いてみました． 興味のある方はご自分で検索してみてください．
Wikipedia によると
Max August Zornだそうです．後に書いた年表によると Zorn の補題は 1935 年ですから，29歳のときですか．研究分野は， 集合論ではなく，抽象代数学， 群理論，数値解析なんですね．1906-1993
Zorn の補題に出てくる順序集合 (P, ≤) は任意のチェインに上限があるから，
が見つかってしまえば，そのもうその上に元を加えることができないようなチェイン C (⊆ P)
P のどれか適当な元 x0 をとって，それから，上にたどっていき，もう上がないところまでたどり着ければ問題ないのだが，なかなかそんなチェインが見つからないかもしれない．
我々の場合は，選択公理を仮定しているので，
というものは存在すると仮定して話を進める．f(x) = x if x が極大 > x otherwise
たぶん，最初の直観は，x0 から f で上に上に行けば良いのではないだろうかという予想を 訴えてくるだろう．(P, ≤) はすべてのチェインに上限があるから，x0 から f(x0), f2(x0), ... と求めて行って，その列と，その上限 ∨ n = 0 to ∞fn(x0) を合わせたチェインが上に極大なチェインの 第一候補となる．
ここで疑問を抱く方もいると思う．つまり，
という疑問である．今までの例で，確かにどれだけでも長いチェインが 発生し得ることを示して頂いた訳だが，結局，どれだけ長くても全部 チェインになっていた訳で，(P, ≤) のチェインには上限があるのだから， 問題ないのではないか？
確かにこれは一理あるのだが，今までの例はチェインの途中で止めたらチェインと いう訳で，まだ上がある場合は「上に極大な」チェインは完成していない訳で， 上限をとって極大元が得られるチェインはまだ得られていないのではないだろうか．
それに対して，
という反論があるかもしれないが，それは極大元が存在するのとほぼ同等のことを 言っている訳で，話は堂々巡りになってるような気がする．だから，極大なチェインになるまで伸ばしてから考えれば良いのではないか？
いや本当はこれで正しいのかもしれない．結局，何とか上に極大なチェインを作ることでしか 証明はできないわけで，ここでの議論を精密化すれば良いのかもしれない．
・・・・・・・・・・・・・・・・・・・・・・・・
こういう，直接，巨大なチェインを構成できないときは，
部分部分を作ってつなぐというよりは，段々伸ばしていったチェインの集合を作り，それらの 和集合を作る方法である．つまり，次の図のように x0 から始めて， より上の元を選ぶ関数 f と上限をとる操作 ∨ で上に 伸ばしていったすべてのチェインの集合 C を考え，その和集合
∨ C
を作ることによって，「上に極大な」チェインを作るのである．
ここでちょっと気を抜いて，集合論のゲームみたいなものをやってみよう．ここのタイトル
では始めよう．
次のような２人でやるゲームを考える．このゲームをやる人を A さんと B さんとする． ゲームのルールは次の通りである．
B さんが持っている集合が有限集合の場合，A さんは毎回一番大きくなった集合を 提示すれば，B さんは新しい元を一つずつ差し出さざるを得ず，いつかは，すべての元を 含む集合が F にできて，A さんが勝つ．
では，
B さんが最初に持っている集合を，すべての自然数の集合
N = {0, 1, 2, 3, ...}
としてみる．
このときは B さんは次々に偶数を出し続けることによって，奇数にはまったく手を 付けずにゲームを続けることができる．A さんは決して F に自然数の集合 N を作ることができない．
それでは再度，
A さんは，F の中の集合の和集合をとって，Fに 入れてよいものとする．この和集合の取り方は，無限個の和集合でもよいとする． なんで無限個の集合が F に入っているのかは，実は，出題者の私も 多少不思議に思うことがある．とにかく，このやり取りを無限回やってよいので， それで出来た無限個の集合の和集合を F に加えて，A さんの 次の番にそれを出せるとするのである．よけい混乱したら申し訳ない．
ここで A さんはおもむろに，偶数全体の集合を提示すると，B さんは何か奇数を 出さざるを得ない．このようにして，A さんは最初の奇数 1 をゲットし，あとは 次々に残りの奇数をゲットしていって，ついには自然数全体をゲットしてしまう．
今まで仮想のゲームの話を自然語で話してきたので，曖昧なところもあったと 思う．そこで，話を数学に戻して，上の話で言いたかったことを少し正確に記述してみる．
X を集合とする．次のような性質を持つ集合族 F には X は含まれるか？
(集合族とは集合の集合のこと）
答えとしては，X ∈ F は成立するのである．実は，
X = ∪ F
となる．つまり，F の全部の集合の和集合をとると X になり，それは上の
３番目の要請から，F の元でなければならないのだ．
もとのゲームの話に戻るが，今，行った数学上の議論から，先のゲームで A さんが最初に 持っていた自然数の集合を実数の集合 R に変えても，A さんが勝つゲームに なってしまう．
実数の集合は自然数の集合より沢山の元が入っているので，本当に長い長いゲームで ある．A さんは新しい元を次々に獲得していって，それらをまとめて新しい集合を 作る．そして作られたそれらの集合を使ってまたゲームを続ける．そしてついには B さんが持っている実数すべての集合を手にしてしまうのだ．
それでは最後にもう一回だけルールを微修正してみよう．
前回のルールでは，A さんは F の中のどんな集合の和集合でも作って 良いことにしていたが，ここで少し制約を加えてみよう．
A さんは， C が ⊆ に関してチェインになっているときだけ， ∪ C を F に加えてよい．
この新しいルールでも，Zorn の補題を使えば A さんは R を F に 加えることができる．つまり，A さんが勝つためには，一般には選択公理を仮定しなければならなくなるのである（最初の集合 S が特殊な集合の場合は選択公理が必要ないこともある）．
同じような絵ばかりで申し訳なかったが，Zorn の補題における集合論の役割を 考えるきっかけにはなったのではないかと思う．実は，この絵は，私が Zorn の 補題の証明をあれこれ考えているときに試してみたことを絵にしてみたものである．
一応，ここでは，
方法での証明を１つ挙げておく．
まず，記号の確認をしておく．この証明の章を通して，f : P → P は選択公理から作った
f(x) = x if x が P で極大
> x otherwise
なる関数とする．これはこの証明を通して
証明は命題と命題の間の数学的推論に殆どジャンプが無いようにしたのと， 非常に基本的な概念だけを 使ったので，かなり長い．それらを追って行く前に，どういう戦略で証明していくのかを 述べる．こちらは本当に短い．その後は，その戦略がきちんと実現できるということを 長い証明で確かめていくだけである．
このような長いチェインを直接作るのは難しそうなので，以前の章
「何が難しいのか(長いチェインを作る証明について）」 で検討したように， 上の元が存在するならそれを選ぶ関数 f の適用と，そうしてできた元の集合の
上限をとる操作の２つで
作成した，
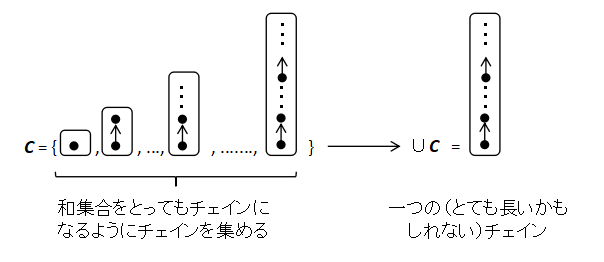
そのチェインは，ゆくゆくは全体の和集合をとって，（とても長いかもしれない）チェインを 作り，その上限をとることで (P, ≤) の極大値を作るチェインの集合である． ちょっと，そのチェインに対する我々の願望をまとめておこう． 願望をきちんと書くと次のようになる．
この２つが満たされたチェインの集合 C が定義できれば，∨(∪ C) が極大元である．なぜなら，∨(∪ C) の上の元 f(∨(∪ C)) は，一番目の願望から， Cのどれかのチェインに入っているはずだから，
f(∨(∪ C)) ≤ ∨(∪ C)
一方，f は自分以上の元を割り当てる関数だから，常に x ≤ f(x)． したがって，
f(∨(∪ C)) ≤ ∨(∪ C) ≤ f(∨(∪ C))
となり，
∨(∪ C) = f(∨(∪ C))
つまり，∨(∪ C) は極大である．
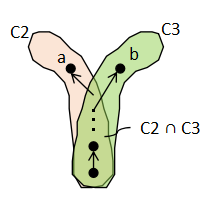
例えば，
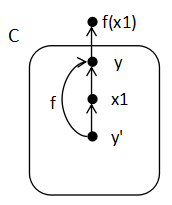
右の図のような状況を考えてみよう．チェイン C1 を真ん中の薄緑に
塗った部分 {x0, f(x0), x1, f(x1)} とし，
これらの元の間の大小関係は右図の点線で示されているとする（点線の上が大きい）．
チェイン C1 が，C に入っていたとする．もし，C の
チェイン C の中の任意の元 x∈C に対して，f(x) を加えたチェインを
加えるという方法で
チェインを伸ばしていこうとすると，チェイン C1 にf2(x0) を
加えたチェイン C2 と
f2(x1) を加えたチェイン C3 が C に入ってきてしまい，
C は，和集合の操作で統合できないチェインの集合になってしまう．
C は次の条件を満たすような P のチェインの集合とする． C の中のチェイン C∈C は 次の条件を満たすものとする．
- C は
整列集合（well-ordered set）である （つまり C の 任意の部分集合 D ⊆ C が最小元 min D を持つ）．- x∈C ならば，
x = x0 またはx = f(x') ∃x'∈C またはx = ∨ {x'∈C | x' < x} このような C としては {x0} があるので，C は空集合ではない*．
* （公理的集合論 ZF で利用した公理が気になる人への補足）
このような集合 C が存在することは， ZF 集合論 の中の，冪集合の公理と分離公理を使っている． つまり，C := {C ∈ 2P | C は上の条件を満たすチェイン}また，{x0} という集合が存在することは対集合の公理 {x, y} が 存在することを，{x0} = {x0, x0} として使っている．
二つ目の条件 1, 2, 3 は，C に属する元は，（どこか特定の元から始まって いれば，それぞれは）x0 から始まっていることを要求している．問題は， 無限降下列があり，いつまで元をたどってもきりがない場合である．つまり，x0 から始まっているのかどうか判定できない場合である．このような 場合がないことを一つ目の条件の「C は整列集合である」で担保しているのである．
こういう C の定義方法は一通りではない．例えば，このページの 終わりに載せてある J.B. Nation 教授の束論のテキストの付録では， 別の条件を使っている．
証明の方法としては 超限帰納法を使うという手 もあり，その場合はここの 証明より短くなる．しかし，ここでは，本当に基本的な推論の列で上のことを 確かめてみよう．そのほうが，起こり得る状態を具体的に認識できるので， 順序集合に対する 我々自身の感覚を磨くことができると思う．
一応，迷子にならないように 証明の全体像 を載せておく．
ということで始めよう．
(∪C)∈C を証明するためには次のことを 証明しなければならない．
まず，C∈C の構造に関する次の２つの命題を認識しておく． これらは後で証明する．
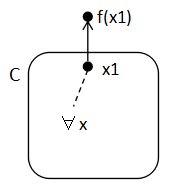
C∈C, x1∈C に対して
f(x1) ∉ C ならば x ≤ x1 for ∀x ∈C
つまり，f(x1) が C を飛び出すなら，x1 が C の最上の元であるということである． 直観的には，上限をとる操作 ∨ は，x1, f(x1), f2(f1), ... の無限列が あって，その上にくるのであって，先ほどの無限列の途中にはこないということである．
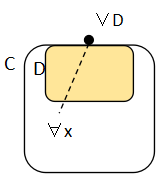C∈C, D ⊆ C に対して
∨D ∉ C ならば x < ∨D for ∀x ∈C
チェイン C ∈C において，途中のある上限 ∨D が C の中に なくて，その上が C の中にある状況は無いということを言っている．もっと直観的にいうなら， ∨D の下の元が f で∨D を飛び越えて上に出るということは無いということである． D⊆C は，x3 を C のある元として，x3, f(x3), f2(x3), ... というような上昇列をイメージ すればよい．
これらを頭において
∀C2, C3 ∈ C に対して C2⊆C3 または C3⊆C2
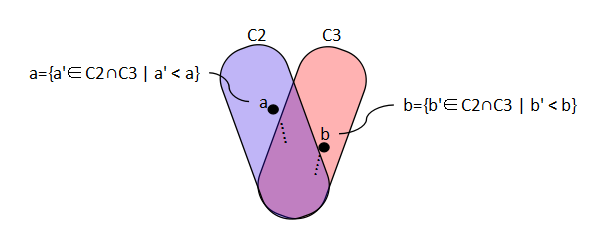
これが示されれば，x, y ∈ ∪C のとき，∃ C2, C3 ∈ C であるから，x, y はどちらも C2, C3 の大きな方に入っており，比較可能になり，∪C は任意の二元が比較可能でありチェインであることが示される．
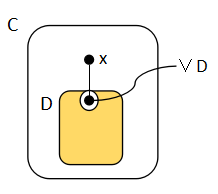
(C, ⊆)がチェインになっているということは，C の勝手な チェイン C2, C3 を取ったとき，次のような状況になっていないということである．
つまり，C2 も C3 も相手のチェインに含まれない元を含んでいるということである． C2, C3 は整列集合であるから，このような元の中で最小元がある．C2 のものを a ， C3 のものを b とする．a, b はどちらも x0 ではありえないから，
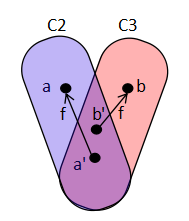命題１をC2, b'∈C2, b=f(b')∉C2 に適用すれば，C2 の元は
みな，b' 以下になるから，a'≤b'．
C2 と C3 の役割を変えて命題 1 を適用すれば，a'≥b'．故に a'=b'.
これは
a = f(a') = f(b') = b
を意味し，a, b が相手のチェインに
属さないということに反する．
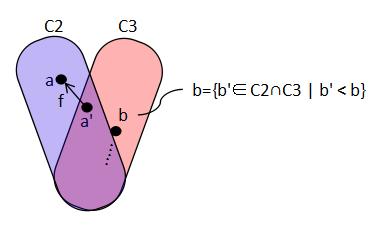命題 1 を C3, a'∈C3, a=f(a')∉C3 に適用すると C3 の元は
みな a' 以下になるから，b≤a'．
一方，命題 2 を C2, b, a'∈C2 に適用すると b > a' が得られ，これらはお互いに
矛盾する．したがって，このような場合はあり得ない．
いま，空集合でない任意の D⊆∪C をとり，これに最小元が あることを示す．D は空でないので，なにかある元 d∈D がある．C の 中で d を含むチェインの一つを C1 とすると，すぐ後で書くように ∪C の d 以下の部分は C1 の d 以下の部分と一致することが証明される．したがって，D の最小元は， もし存在すればそれは D ∩ C1 の 最小元と一致し，後者は整列集合 C1 の部分集合なので，最小元が存在する．
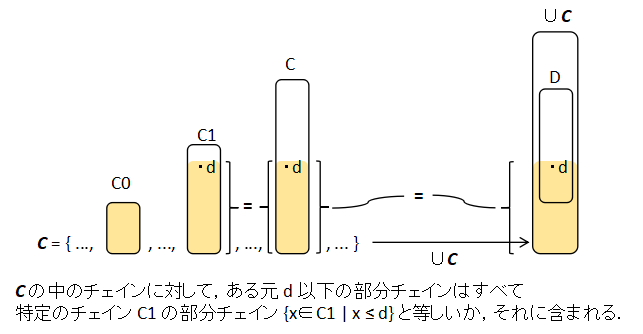
上で仮定した
∪C の d 以下の部分はC1 の d 以下の部分と一致すること
を示す．
まず，C∈C の中で，d を含まないものは，(C, ⊆) がチェインであることから，C⊆C1 であり，和集合の中では無視して構わない．
d∈C とする．このとき次のような二つのチェインを定義してみる．
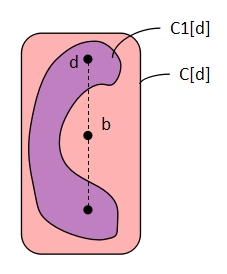これらはともに d を最大限とする C のチェインである．
C のチェインはお互いに包含関係があるので，これらが
一致しない場合には，片方に，もう片方には無い元がある．これを右の図の
ように b∈C[d] としてみよう．b は最小にとっておく．
b が b=f(b') b'∈C1[d] の場合は，C1[d] の元は全部 b' 以下になり，
d も C1[d] の元であるから，d ≤ b' < b=f(b') となるが，これは d が C[d] でも
最大であることに反する．また，b={b'∈C[d] | b' < b} のときは，C1[d] の
元はみな b より小さくなり，この場合も d が C[d] で最大であることに反する．
したがって，
C1[d] = C[d]
が得られ
{x∈C | x≤d} = C1[d]
であることがわかる．したがって，D の最小元 は D∩C1 の最小元と等しく，後者は
C1 が整列集合であることから存在する．故に，∪C の任意の
部分集合 D が最小元を持つことから ∪C も整列集合である．
x ∈ ∪C ならば
- x = x0 または
- x = f(x') ∃x' ∈ ∪C または
- x = ∨ {x' ∈ ∪C | x' < x}
x∈∪C とする．このときあるC1∈C が存在して， x∈C1である．したがって，
これですべてが証明された．
C∈C, x1∈C に対して
f(x1) ∉ C ならば x ≤ x1 for ∀x ∈C
もしこのような x < y < f(x) が存在したなら，C が整列集合であることから，
そのような x の最小元が存在するので，x をその元にしておき，y もこの関係を満たす
最小元とする．このとき， y∈C だから，y=x0 または，y=f(y') ∃y'∈C
または y={y'∈C | y' < y} であるが，x < y < f(x) の関係から，
y=f(y')のケースしかあり得ない．
y' < x < f(y')
が最初に述べた関係を満たすことになり，x の最小性に反する．したがって， チェイン C の中では
x < y < f(x)
となる2つ組はない．
f(x1) ∉ C for ∃x1∈C かつ x1 < y for ∃y∈C
が成立したとする．C は整列集合で あるから，このようなx1 の最小のものが存在する．また，y もこの関係を満たす 最小元ととっておく．このとき，上と同様の議論から，y'∈C が存在して，
y' < x1 < f(x1)
という関係にならねばならないが，これは上で証明したようにあり得ない．
これで命題１が証明された．
C∈C, D ⊆ C に対して
∨D ∉ C ならば x < ∨D for ∀x ∈C
命題2が成立しないとすると，x∈C で，∨D と比較不能のもの， あるいは，x > ∨D なるものが存在する．
x が∨D と比較不能としてみる．このとき，D の元は C に入っているので x と比較可能である．もし，D の元で一つでも x 以上のものがあれば， ∨D はそれ以上なので，x ≤ ∨D となり，比較不能ではない．また， D のすべての元が x より小さければ，x は D の上界であり，∨D は， D の最小上界であるから，このときも比較不能にはならない．
x∈C で，C は整列集合であるから， x>∨D の最小元がある．x をそのような最小元としてとっておく．x∈C であるから，
x' < y < ∨D < x
となる4元 x', y, ∨D, x が存在することになり，このうちの x', y, x は C の元になるが，これは命題１の証明で述べた関係にあり，あり得ない．したがって，C の中に ∨D より大きな元は存在しない． これで命題2が証明された．
C ∈C の条件として
- C はチェインである
- x0∈C
- x0≤y for ∀y∈C
- もし A が C の空でない order ideal で z∈C∩(Au - A) ならばγ(A)∈B∩z/0
ここでAu = {x∈P | x ≥a for ∀a∈A}
γ(A)=φ(Au - A)
φ(A) は，空でない集合 A からその要素のどれかを返す選択関数
z/0 = {x∈P | x≤z}
A が順序集合 P の order ideal であるとは，A⊆P が，x∈A, y∈P かつ y≤x ならば y∈Aを満たすことである．
∪C ∈ C を示すために，本ページでは 非常に長い証明を行った．これは超限帰納法を使うことである程度短くできる．それは， いま，チェイン C に対して C(x) = {y∈C | y < x} と書くことにして， C2, C3 ∈ C ならば
のどれかのケースしかないことを超限帰納法で証明する方法である． このときの証明の流れを下図に示す．
本ページでは， 順序集合に対する我々自身の感覚を磨くために敢えてイバラの道を選んだ．
Tukey の補題は，
A を集合，F ⊆P(A) = 2A を A の部分集合のある集合とする．
集合族 F が
X ∈ F <=> X の有限部分集合がすべて F の元である
が成立することである（<=> は論理的な同値を表す）．
この定義は少し分かりにくいかもしれないが，次に Tukey の補題を述べた後に 有限の性質を持つ集合族の例をいくつか挙げる（その方が説明の効率が良いので）．
この定義の下に Tukey の補題は次のように述べられる．
A を集合，F ⊆P(A) = 2A を有限の性質を持つ集合族とするとき， F には ⊆ に関して極大元がある．
それでは，有限の性質を持った集合族の例を挙げる．
なぜなら，C0 ∈ C つまり，C0 がチェインであるというのは，C0 の有限部分集合がすべてチェインであるとき，かつ，そのときに限るからである．特に，有限部分集合として， ２つの元からなる部分集合 {x, y} がチェインであるということは，∀x, y ∈ C0 が比較可能 であるということを意味している．また，任意の２元が比較可能なら，C0 の有限部分集合は チェインである．つまり，本質的なことは，任意の２元が比較可能であるということである．
C0 ∈ C の代わりに，「C0 がチェインである」と言うことにすると，
C0 がチェイン <=> C0 のすべての有限集合がチェイン
<=> ∀{x, y} ⊆ C0 がチェイン
<=> ∀x, y ∈ C0 が比較可能
となるので，C0 が普通の意味でチェインと同じ意味であることが分かるだろう．
ということで，この集合に Tukey の補題を適用すると，
ことになる．もし，(P, ≤) が，すべてのチェインに上限がある順序集合なら，P の極大なチェインの一つ C1 の上限 ∨C1 が，P の極大元となり，
A(G) := {A ⊆G | xy = yx ∀x, y ∈A}
とする．A(G) の中の集合 A ⊆ G は群とは限らないが，要素がお互いに可換である． A(G) は有限の性質を持つので，Tukey の補題から 極大元 H ∈ A(G) を持つが，H はその極大性から，次のように群になる．
(ab)c = a(bc) = a(cb) = (ac)b = (ca)b = c(ab)
となり，ab は H の全部の元と可換なので，極大性から ab ∈ H
a-1b = a-1b (aa-1) = a-1(ba)a-1 = a-1(ab)a-1 = (a-1a)ba-1 = ba-1
となり，H の極大性から a-1 ∈ H
ということで，無矛盾な論理式の集合族には極大集合がある．すなわち，もう これ以上論理式を（公理として）加えると矛盾してしまうというギリギリの ところがあるのである．この事実は計算機科学でも記号論理学を学習する 上で非常に役に立つ感覚を育成すると思う．
X を集合，R を X 上の n 項関係とするとき，n 個の要素の組が 全部 R を満たすような Y ⊆ X には極大集合があるn-項関係 R は１個だけでなくとも，複数個あって，それらが同じ 個数の引数を取らなくても，有限個の要素の関係ならこれは成り立つ． 群の中の極大可換群，論理式の集合の中の極大な無矛盾集合はこのタイプで ある．
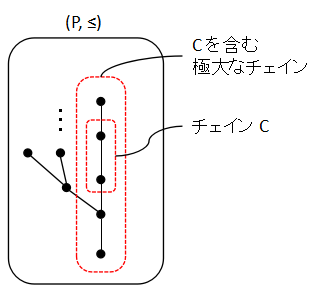
(P, ≤) を任意の順序集合とし，C⊆P を P の任意のチェインとする． このとき，C を含む極大なチェインがある．
ここで極大なチェインとは，もうこれ以上の元を加えると
チェインでなくなってしまうようなチェインである．
最初のチェイン C の指定をなくして，
順序集合には極大なチェインがある
我々は，Zorn の補題の証明で，上に極大なチェインを作るのに四苦八苦した． この命題があれば，上に極大といわず，とにかく極大なチェインがあるので， その上限が P の極大元になり，あっという間に Zorn の補題の証明が終わってしまう． 結構，強力な原理であることがわかると思う．登場する順序集合に特に条件がついていないのも 私は好きだ．
私自身は計算機科学の分野で長いこと仕事をしてきたので， やはり選択公理を使うか使わないかは大いに気になる．使わないで済むなら 使わないし，また，日ごろ使っている定理が，選択公理にどの程度「汚染」されて いるかは気にかかる．
ここには選択公理に類する公理，命題の情報を集めておく．私自身のメモの ような意味で設けた記述なので，あまり読む人への配慮はしていない．
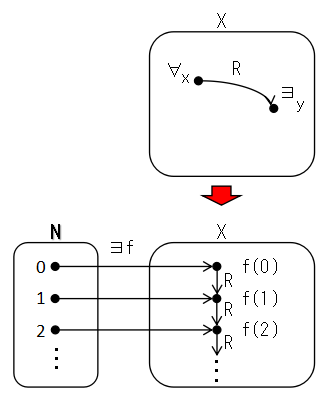X を集合，R を X の上の entire binary relation とする．このとき
自然数の集合 N から X への関数 f :N→X で，
f(n) R f(n+1) for ∀n∈N
となるものが存在する．ここで二項関係(binary relation) R が
∀x∈X ∃y∈X (x R y)
が成立することとする．
命題「整礎集合でなければ無限降下列がある」，対偶をとれば， 「無限降下列の無い順序集合は整礎集合である」の証明にはこれが必要．
ZF集合論のもとでは Löwenheim-Skolem の定理と同値らしい．
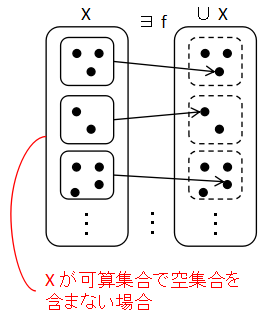
集合 X が空でない集合の可算個の集合であるとき，X には選択関数
f : X→∪X
f(x)∈x for ∀x∈X
が存在する．
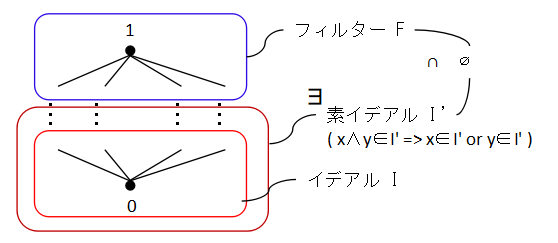
B をブール代数， I⊆B をイデアル， F⊆Bをフィルターとし，I∪F=∅ とする． このとき，I を含む素イデアルで F と共通集合を持たないものがある．
用語や関連命題など：
どういう応用かというと，部分関数をたくさん集めて，それらを合わせて全域関数を 作るという応用である．
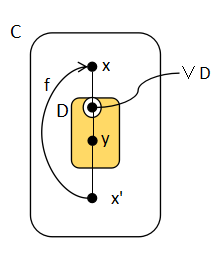
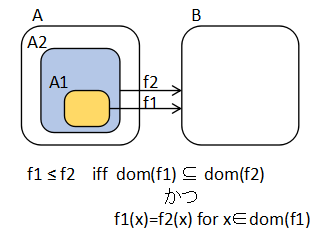
集合 A から集合 B への
PFun(A, B) は次の定義で順序集合になる（右図を参照）．
f1 ≤ f2 iff dom(f1)⊆dom(f2) かつ f1(x)=f2(x) ∀x∈dom(f1)
計算機科学では（たぶん，数学でも）局所的に定義された部分関数をたくさん集めて
全域関数を作りたいことがしばしばある．このような応用に対して，選択公理とZorn の
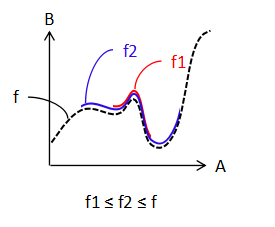
補題がどのように寄与するかを示したのが次の図である．
左が選択公理を使ったときの利用である．すでに関数が領域 A1 で定義されているとする． 選択公理の利用では，さらにどんな点でもA1での定義と互換性のある関数定義が可能なら 全域の関数が存在することが保証される．つまり A - A1 のどの点ででも，お互いに 独立に関数の値を決められる状況で全域に拡張できると言っている訳である．
それに対して，Zorn の補題では，すでに与えられた領域それぞれに対して， 拡張できる点が １点でもあれば，関数を集合 A 全域に拡張できると言っているのである．このとき すでに領域に加えた点によっては次に拡張できる点が限定されてしまうかもしれない． しかし，一点でも拡張できる点があるならば全域に拡張できると言っている．
これはずいぶん選択範囲が限定された状況で利用できるのでとても有難い． こういう強力さが Zorn の補題が多用される理由だと思う．
P.S. この∀と∃の同値対応は，ガロア接続や随伴関手（Adjoints）の香りがする． そのうち考察してみたい．
関係と関数はどこが違うかというと，
この問いに対する一般的には答えは私にはないが，Zorn の補題の我々の証明の 中では，関数性は次の箇所で寄与している．
つまり，上の元を与える操作に関数性があるおかげで，決まった１つの長いチェインの 部分だけを集めることができていて，それらを和集合操作で合成することが できている訳である．これが複数の候補を出してくる関数（関係）だと， 少なくとも我々の証明ではうまく行かない．
特徴的なところは最後の文言「上の規則で作られたものだけが〇〇である」である． こういうスタイルの定義は数理論理学や形式言語理論，λ計算などで よく使われている．このスタイルは〇〇に関する性質を 証明するとき，構造に関する帰納法を使うことの根拠になって， とても便利である．自分自身でも多用していたのだが，今回の Zorn の補題の 証明で苦しんでいて，この文言の使用に疑問を持った．
今回の Zorn の補題の証明は，基本的には x0 ∈ P から，上の元を与える 関数 f とその部分集合の上限を与える操作∨で上に伸ばしていったチェインの 集合をきちんと定めることがポイントである．そのとき，x0 以外から始まる チェインを除外するのに苦労した．しかし，もし，上のような 「上の規則で作られたものだけが〇〇である」が許されるなら話は簡単である．
とすれば良いのである．
私が，「上の規則で作られたものだけが〇〇である」スタイルの定義に疑問を 持ち始めたのは，これが２階の記述だからである．つまり，記述される対象の 性質を述べているのではなく，その記述に関した言及を含んでいる点である． たぶん，これは一階述語論理では書ききれないであろう．もし書けるとしたら， 〇〇である集合の基数を例えば可算集合に制限することができることになるが， これは下に注釈を書いたレーベンハイムスコーレムの定理から無理である．だから，きっと この記述は少しメタな記述になっていて，利用には細心の注意が必要なのに 違いないと思う．そういえば，最近，あまり，この手の記述を見なくなった ような気がする．気のせいかもしれないが．
「上の規則で作られたものだけが〇〇である」と同様な記述で，
〇〇を満たす最小の集合
という表現もある．こちらは完全に１階述語論理で表現可能である．上の 「上の規則で作られたものだけが〇〇である」はこちらに翻訳できる場合も あるだろう．だから常に２階の表現になるとは限らない．安全に使える条件と いうものがあると良いなと思う．
注意：レーベンハイム・スコーレムの定理
一階述語論理で記述された公理系がモデルを持つなら，そのモデルの要素を絞り込んで， 可算無限個の要素からなるモデルを作ることができる（ダウンワード・レーベンハイム・ スコーレムの定理）．また同様に，任意の無限基数に対してその基数のサイズのモデルに 作り変えることもできる（アップワード・レーベンハイム・スコーレムの定理）．ということで 一階述語論理での記述では，モデルの基数を制御することができない．これに対して， 「上の規則で作られたものだけが〇〇である」は，例えば，そうやって定義した集合が 可算無限個の基数を持つことを強いる可能性があるように思える．従って，一階述語論理に 閉じた話をしたいときは，これを使わない方が良いのではないだろうかというのが 今の私の気持ちである．
選択公理のやっていることは，やっぱり，一番最初に，各元が極大元でなければ，より上の元を
まあ，一応，修飾詞を入れると，
で，この選択公理が問題があるかどうかだが，きっと今までいろいろな人が議論して
きたことなんだと思うが，基本的には，私は
基本的には人間に無限の操作はできない（と思う）．有限の世界の中で暮らしている． しかも，有限の中のごくごく小さな 数のところで活動している．帰納関数の中には急速に大きくなり，あっという間に， 認識できる宇宙に存在する粒子で２進数を作ったくらいでは到底表現できない数になってしまうものが いくらでもある．そのような関数を我々は表現可能，操作可能というのだろうか． 単に有限の理論を作るとあちらこちらで記述に制約ができてきて，面倒が増えるので 無限を考えているだけではないだろうか．計算理論でも，一部の人たちは， チューリングマシンのようないくらでもメモリーを増やせる機械を考えるのは 有限の世界に生きている人間には無理があるので，有限オートマトンをベースに して計算理論を作り直せと言っている．
と言いつつ，ことがチューリングマシンやオートマトンなどの，自分に身近な
計算理論に及ぶと，やはり，
この節は比較的重要であり，ページの後ろに置くのはあまり格好の良いものではないが， 目次から飛べるようにしているのでご容赦願いたい．
本ページの大部分では，上に極大なチェインを求めるのに，１つの元から次の２つの 上昇原理を使ってチェインを上に伸ばしていっている．
証明では，この二つの場合を区別して述べているため，量がかさんで読みにくくなっていると 思う．
一方，選択関数を，次のように P の中のチェインから P の元を割り当てるように とってみる．C を P のすべてのチェインの集合とする．
g : C → Pg(C) は，P に C の中のどの元より大きい元があればそのうちのどれか， なければ C の上限（これはZorn の補題の仮定から存在は保証されている）． 具体的には，上の f を使って，
g(C) := f(∨C)
として置けばよいだろう．
実は，このような関数 g : C → P を考えた段階で P の各元 x に対して，そこから極大元まで登っていく整列集合が定まってしまうのである． つまり，最初は，x だけからなる集合 {x} で，次は {x} ∪ {g({x})} でという具合に， 次々に出来た集合に g を適用した元を加えていく．このようにして作られた無限上昇列に 対しても g は定義されているので，上限 ∨ を個別にとらないでも上昇列は 一意に定まる．また，これは整列順序になっている．このように，選択公理を使った f や g から１本の長いチェインが定まるというのは，f や g の関数性に寄っている． つまり，任意の元 x や任意のチェイン C に対して，f(x) や g(C) が一意に定まるので １本の整列集合が定まるのである．
これは任意の集合に対する整列可能定理の証明でも同様である．整列可能定理は 任意の集合に整列順序を導入できるという定理であるが，A を最初の集合とし， A の任意の真部分集合 B に対して，A - B の元を与える選択関数 h を決めた 段階で∅からはじめて A のすべての元を取りつくす列がきまり，取り出した 結果をその取り出された順序で順序つければ整列順序が出来上がる（容易に わかると思うが，元（げん）を取る列そのものが結果の整列集合と同型の整列集合になる）． この場合の選択関数 h と整列順序は同一のものと言っても良い．
この整列可能定理については
に書いたのでよければ参照してほしい．話を戻して，このページでは上に極大なチェインを求める方法を二つの上昇原理として理解し， 延々と述べて行った． 一般的にこのようなアプローチが本当に必要かどうかは自信がないが，自分自身に ついて言えば，一時，このような個別の場合分けまでどっぷりつかり， 順序集合や整列集合の細かい部分を使う練習をしたことは良かったと思っている．
上の考察２では，順序集合 (P, ≤) の中のチェインを上に昇る方法として二つの方法を述べた．
このページの証明では
しか作れるような{x, f(x), f2(x), f3(x), ...}
このページでは，幕間のゲームの話も含めて，「f でチェインを上昇する」など，人の 操作イメージに結び付ける表現が多かった気がする．有限回の操作は有限長の証明と 書けるので操作に結びつけてもそれほど問題はないが，無限に関することは何らかの 公理に結びつけて証明として裏付けする必要がある．
と言うことで，ここではとにかく，上で出てきた次の２つの疑問点に関して，そのような裏付けを取っておこうと思う．
以下，それぞれについて述べる．
ここでは次の図の(1) と (2) の同値性を ZF + Zorn の補題の条件のもとに言えば良い．
ZF の公理系がどのようなものか知らない読者もいると思うが，この段階では あまり詳しい ZF の知識は要らない．
とりあえず，上の図の①と②の矢印を証明しておく．
g(C) := f(∨C)とすれば，望む g が得られる．チェイン C の上限 ∨C は Zorn の補題の条件から，常に存在が保証される．
f(x) := g({x})とすればよい．{x} は ZF から集合として存在することが保証され，また，これはチェイン でもある．したがって，{x} が極大のチェインでない限り，f(x) = g({x}) > x である．
これで，少なくとも ZF + Zorn の補題の条件の下では f と g の存在は 同値であることが保証された．
ここで示すべきことを
要素への f の繰り返し適用と，そうしてできたチェイン C に対して 上限 ∨C を取る操作で P の中のある上に極大なチェインに到達できることとしてしまうと，それは Zorn の補題そのものであり， このページで一生懸命証明したことなので，ここではそれを繰り返すのではなく， ZF と Zorn の補題の条件のもとで，
ことを説明していくことにする．この操作を「任意回数」，つまり，有限回数，可算無限回数，それ以上の集合の基数回数 繰り返したチェインが作れる
ここでは ZF に関するある種の知識が必要になってくるが，それはその場面で 説明することにする．ZF の公理について詳しく知りたい人は，私が以前，ある勉強会で 発表してきた資料
某勉強会での Alternative Set Theories の発表 PDFの中に，ZFC についてまとめた章（「公理的集合論ZFCの概要」 2019年８月18日（日）修正版で pp27-35）があるので，そちらも参照されたい．
まずは有限回の f の適用ができることは自明だろう．
{x, f(x), f(f(x)), ..., fn(x)}と有限回書き下せば良い．
次に，自然数の集合 N に対して
C1 := {fn(x) | n∈N}を作ることができることを示す．
これには多少の ZF の知識が要る．ZF には
φ(x, y) が，φ(x, y1) かつ φ(x, y2) なら y1=y2 を満たすような述語で あり，A が集合なら，
B := {y | φ(x, y) for x∈A}も集合である．
φ(x, y) は x に対して高々１つの y しか φ(x, y) を満たさないので，関数の記法を 使って， この y を F(x) と書くと，B は
F(A) := {F(x) | x∈A}というような集合である． （正確にいうと φ(x, y) となる y が存在しない x もあるかもしれないので， 関数というよりは部分関数であるが，直感的には集合の要素に関数を適用した結果を 集めた結果は集合になるという公理ととらえておく）．
プログラミング言語での例えで 言うと，置換公理で作られる集合 B は関数型言語でのリストに map 関数を適用した ものである．
map([x1, x2, ...], f) = [f(x1), f(x2), ...]
一応，置換公理を論理式の形でも書いておく．
∀x,y1,y2 (φ(x, y1) ∧ φ(x, y2) → y1=y2)
→∀A ∃B ∀y (y∈B.∃x (x∈A ∧ φ(x, y))
この置換公理と，これも ZF の公理であるが，
自然数の（無限）集合 N が存在する．
ここに N は次の性質を持つ集合である．
（N はこのような性質を持つ集合のうち，最小の集合としておく．）
という公理を使うと，
C1 := {fn(x) | n∈N}の存在が言えることになる．もっとも，n から fn(x) へ対応付ける関数が存在すると いうことは，正確には再帰の原理を使わないと証明できないということと， その再帰の原理にも，置換公理が使われているということは留意する必要がある．
Zorn の補題の条件からC1 の上限 ∨ C1 の存在も言えるので， その上限に f を繰り返し適用して得られる無限集合
C2 := {fn(∨C1) | n∈N}の存在も言える．これはどこまででも続けていけるので，ωをNに対応する順序数とするとき，
0, 1, 2, ..., ω, ω+1, ω+2, ..., 2ω, 2ω+1, 2ω+2, ...の列に対応する f の適用列も作ることができる．
この列は，ZF の次の公理を使うともう少しきちんと作ることができる．
x が集合の集合なら，∪x = ∪y∈xy は集合である
（（注）ZF には集合しかないので，「x が集合の集合なら」は本来要らない 条件であるが，ZF に不慣れな人もいると思ったのでつけておいた）
これは ∪{{a}, {b, c}, {a, d}} = {a, b, c, d} のように中の{} を解いた 結果も集合であるという公理である．
h(n) として，
h(0) = {x, f(x), f2(x), ...}が再帰的に定義できるので，
h(n+1) = {∨h(n), f(∨h(n)), f2(∨h(n)), ...}
∪ h(N)が
0, 1, 2, ..., ω, ω+1, ω+2, ..., 2ω, 2ω+1, 2ω+2, ...に対応する f の適用列ということになる．
しかし，ここまでで出来たのは可算無限回の f の適用だけである．
では，非可算回数の f の適用列はどのようにして作れるだろうか？
置換公理を使うとすれば，集合 A として
A = {∅, S(∅), S(S(∅)), ..., ω, S(ω), S(S(ω)), ...} ただし，S(x) は，x の次の順序数を返す関数．具体的には S(x) := x ∪ {x}
かくして，この集合 ω1 と置換公理を使って，f を非可算無限回 x に 適用していったチェインを作ることができるという訳である．
また，このような順序数は 任意基数の大きさのものがあるので，それを使えば，どんな基数についても，その基数の 回数だけ f を適用したチェインができる．
ということでメデタシ，メデタシである．
上の非可算無限回数の f の適用列ができるという話では，全然，非可算無限回数の 「...」が具体化した気がしない．単に，
f の代わりに非可算無限回数 S を適用する無限列があるので， 置換公理で，その S を f に置き換えろと言っているにすぎないのではないか？ f の適用で，無限に続く「...」の中にはあるところで，可算から非可算に 切り替わる，種類の違う「...」があると期待したのに，そこが分からないじゃないか．
自然数の集合 N のときは，「なるほどそうか」と一旦は思ったけど， これも非可算無限回の S の適用と同じカラクリなのではないか？ 単に
{∅, S(∅), S(S(∅)), ...}という無限集合があると言っているだけで，「...」がどうなっているかは なにも言っていない．有限にいくら続けても無限まで届かないので， そのギャップを埋める公理が欲しいのだけど，与えられたものは，
無限に続けたものがあるという公理だったというのではあまり良く理解できた気がしない． こちらも，感情的には，有限の部分の「...」，無限になりかけの「...」，そして 無限になってしまった「...」があってほしい．なんか，有限から突然無限になって しまった．でも，本当のところ，そんなものなのかもしれない．
ここでは，ZF の置換公理の利用により，可算無限回数，さらに非可算無限回数 f を適用してチェインを作る「...」のメカニズムを説明した（ハズ）．
ちなみに，ここまで置換公理を持ち上げておいてではあるが，整列可能定理や Zorn の補題は，ZFC でなくとも，Zermelo の集合論（置換公理の代わりに，それより弱い分出公理が ある体系）で証明できたはずなので，f の適用による非常に長い（非可算集合の） チェインの存在自体は，置換公理なしに証明できるはずである．
尚，年表の色はほぼ10年毎に変えてます．また，選択公理は AC (Axiom of Choice) と略しているところもある．
任意の整列部分集合に上界がある順序集合には少なくとも１つの極大元があるというものである（文面上，ここの命題より強い）．
証明の方法は，
もし極大元がなければ，選択公理より，任意の整列部分集合 C に 対して，そのすべての要素より大きい要素を対応させる関数 g(C) があるが， この関数 g を空集合 ∅ からはじめて，次々に今まで適用してできた値からなる 整列集合に適用して新しい整列集合を作ると，上界のない整列集合ができて しまうというもの（要約すれば）．
もともと，1950 年に Hellmuth Kneser により発表された証明であるが，あまり知られて いないので，改めて紹介するとのこと．
上の著者と論文の名前 + PDF 位で検索すると，この論文の PDF が見つかると思う．
この本では Zorn の補題のために章が設けられ，pp61-72 の 12 ページで説明している． 証明の仕方は，チェインに次々にそれより上の元を加えて行って沢山のチェインを 作り，それらの和集合をとるという，このページでも考察した方法によっている． Tukey の補題に関する説明もある．
集合，位相，論理など へ
圏論を勉強しよう へ
束論を勉強しよう へ
半群論を勉強しよう へ
ホームページトップ(Top of My Homepage)
