半群の構造(Structure of semigroups)

第３章は主にグリーンの関係(Green's relation)について書かれています．
(This page gives an intuitive image of green's relations of semigroups.)

グリーンの関係の定義を知りたい人はこちらの解説を 参照してください．

グリーンの関係は半群の構造を知る上でとても重要らしいですけど， 定義からだけではなかなかそれがどんなものか想像できません． そこで，ここでは比較的小さな半群で あるT₃のペーパークラフトを作ってみました．T_n は{1, 2, ..., n}から自分自身への 写像の集合ですね．T₃ は {1,2,3} を {1,2,3}に写すわけですから，3³個=27個の 写像からなります．
(We made a paper craft of relatively small monoid T₃, the whole transformations of the set {1, 2, 3} to itself.)

Greenの関係のペーパークラフト(Paper craft of Green's relation)

次の写真は私が作ったT₃のグリーンの関係のペーパークラフトです． ピンボケで申し訳ありませんが，そのうち撮りなおすかもです (I am sorry for the out-of-focus pictures)． 型紙はこれ(paper pattern)です．

• T₃ from Upper Front1
  T₃ は3つのフロアからなる３階建ての構造をしています．各フロアはDクラスです．同じフロア，あるいは，上のフロアから下のフロアへは写像を左右から作用させることで行けます．
  (This is composed of three floors(D-classes).)
  

  型紙を見れば分かりますが，各フロアの見取り図はこんな感じです (Layouts of Floors)．四角の上に書いてあるのは写像のイメージで，左側に書いてあるのが写像のkernelです（Images of map are written up-side and the kernels are written left-side.）．
  

• 真横からみた図です．(Horizontal view)
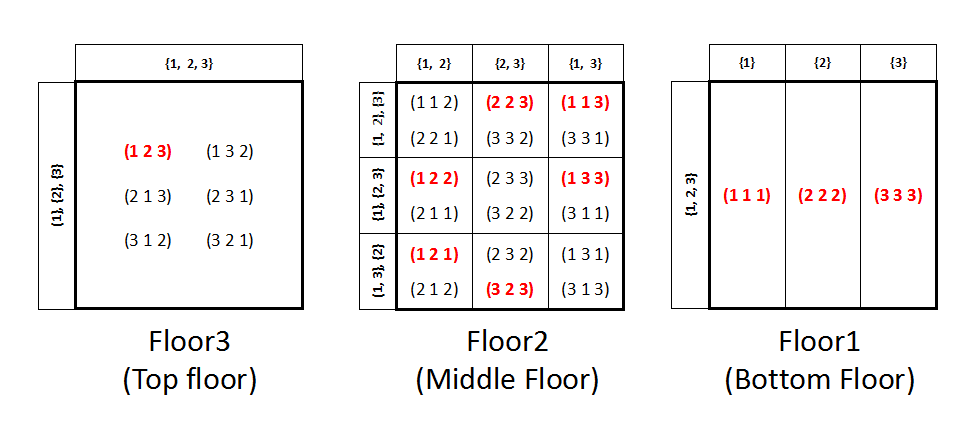
  左側にはkernelの束，右側にはImageの束からボトム（空集合）を取り除いたものが描かれています．
  (The lattice of kernels in left side, the lattice of images minus empty set in right side)
  
  
• ではT₄はどうなるでしょう？(How looks like T₄)
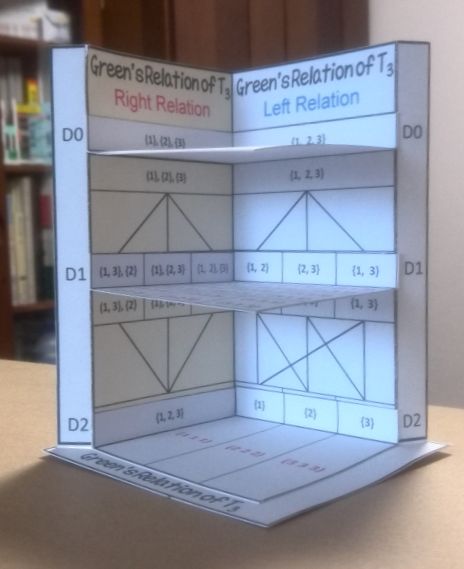
  T₄ は４階建ての建物で，４つのDフロアからなっています．
  (T₄ is a building composed of 4 floors(D-classes))
  Green's relation of T4 (In this data, we used {0, 1, 2, 3} insted of {1, 2, 3, 4})
  
• ではどんな半群のグリーンの関係もn階層のD-フロアからなっているのでしょうか？
  (Any green relations of any semigroups has one D-class at each floor?)
  違います！(No!)
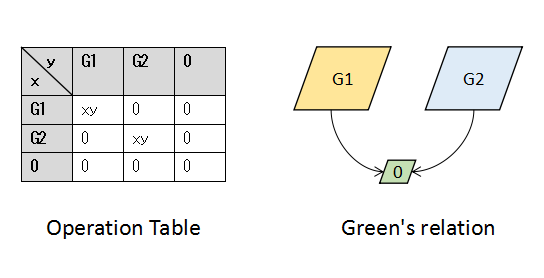
  例えば，お互いに素な２つの群G1, G2に0元を加えて，G1同士，G2同士の積は元の定義通り，それ以外は全部0にした半群のグリーンの関係は下のように，0だけからなるフロアの上にG1とG2が載っている形になります．
  (For example, let G1 and G2 be groups. (G1 + G2)⁰ with xy := xy if both x and y are in the same Gi, 0 otherwise, has the structure below)
  
  Tnは全部の写像が入っているために小部屋が皆つながっているのです．
  (Because Tn is FULL transformation monoid, all mappings are in Tn, and all small rooms are connected in one floor.)
• いくつかグリーンの関係のサンプル(Some Samples of Green's Relations)
  1. ２進化４進数を受理するオートマトンの半群
     (Semigroup of the Automaton that accepts Binary-coded Quaternary)
  2. D-class が沢山あるもの
     (Sample with many D-classes)
• 半群ではありませんが，ペーパークラフトとしては，ほかにも
  (We have further some paperscrafts other than semigroup crafts)
  
  1. 三気筒式高級米田のレンマ 1/17.5 モデル
     (Three cylinders high quality Yoneda's lemma 1/17.5 Model)
     本当は二気筒でも良いのですが，三気筒の方がパワーが出るのです．
     (High power model beyond the normal two cylinders Model)
  2. 観音開き高級随伴関手のペーパークラフト
     (Double doored high quality Adjunction Model)
  などがあります．ただし，こちらは，将来，型紙を１枚30円位で売ろうと思っているので公開できません．
  (It is regretable that I cannot open them here because I would sell them about $0.3 per one paper pattern)