ガロア接続, Closure, 形式概念分析 (Formal Concept Analysis), Abstract Interpretation
これはチュートリアル.探せば Postscript で見つかります.残念ながら,PDF では見たことがありません.
これもチュートリアル.内容は以下の図の通り,だと思う.目次やら内容やらを 斜め読みして適当につけた表紙です.大きく見るためには図をピックしてください. クロージャーとは,例えば,位相空間で,集合に対してその集積点を加えて 閉集合にするような操作です.大学1年生の「集合と位相」というような教科で ちょっとだけは出てくると思います.これと反対に開集合にする操作をカーネル操作と 言います.どちらにしても,位相が決まればクロージャー操作(カーネル操作)が 決まり,その逆もしかりです.クロージャーの概念は位相空間だけでなく,例えば, 概念集合の階層構造を表現する形式概念分析など,いろいろな領域で使われます.

一応,言葉でも説明しておきます(図に書いてあることを自然語にするだけですが).
最初に19世紀からのクロージャーの歴史が章があります.これはすでにある程度内容を 知ってないと読めません.著者も,予備知識が無い人は次の章を読んでからこちらに戻ってくれ と書いています.
次は集合論的な閉包操作と古典的な設定でのクロージャーシステムの話があります. クロージャーの基礎的な知識がここで示されます.
次は順序集合的な設定でのクロージャーの理論です.クロージャー操作(閉包操作)と ガロア接続,随伴(Adjunctions)の相互関係が説明されます.随伴(Adjunction)は 次の章でも説明される圏論の概念です.実は順序集合は圏と見ることができます. ガロア接続は順序集合を圏としてみたときの随伴の関係になっています.
最後に,クロージャーを圏の立場から見たときの話があります.ここでは拡張された 束論的な設定で完備なクロージャーのなす代数について説明があります. このような見方をすることにより,古典的な問題はより透明に,澄んだ見通しが可能になり よりエレガントな解法が可能になります.
この著者はイラストが上手で漫画っぽい挿絵がところどころあります.
これもチュートリアル.上と同じようにガロア接続などのことが書かれています.こちらは かなり計算機よりの話で具体例が沢山書いてあります.
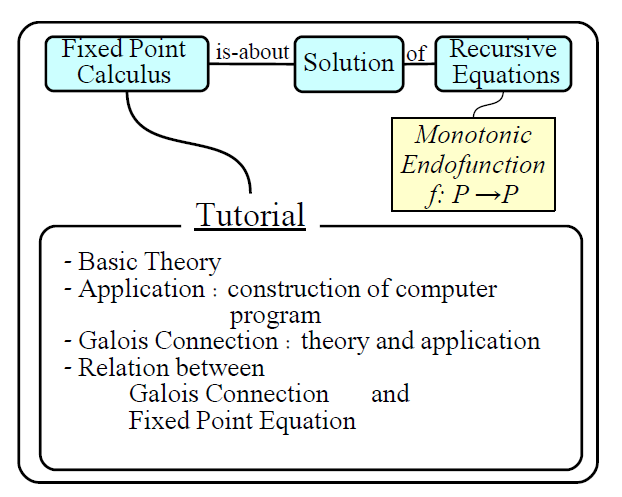
アブストに書いてある程度の概要ですが,上の図に書いたようにものです.すなわち, 不動点計算 (fixed point calculus) というのは順序集合の自己単調関数 f : P → P の解に関する 理論のことです.ここでは,この理論のチュートリアルとして,
- 基礎理論
- 計算機プログラムの構成に関する応用
特に - ガロア接続に関する理論と応用
- ガロア接続と不動点計算
Galculator は Galois 接続を利用して任意のドメインでの証明を導出するツールだそうです. これと,Point free transform および Indirect equality principle を組み合わせれば,プログラム検証の複雑な証明に対する強力で汎用的な道具になるということです.この論文ではガロア接続の性質から導出された書き換え規則を Haskell で書いた Strategic rewriting system のプロトタイプに入れることで証明を生成することができることを示します.また,この論文では, Galculator とそのほかの証明支援システム,例えば,Coq と統合する展望を議論します.
ソフトウェアの可変性を表現する概念束だそうです.ソフトウェアの可変性とは,例えば, 似たソフトウェアをたくさん作らないといけないとき,その一部をパラメータ化して, そこだけを変更することにより,それらのソフトウェアを作るようなことを意味します. 短い論文です.
解説です.貴重な日本語の解説.
ソフトウェアの意味論に関係していて,ガロア接続を活用してソフトウェアの検証などを行う技術です.
オートマトン,言語理論
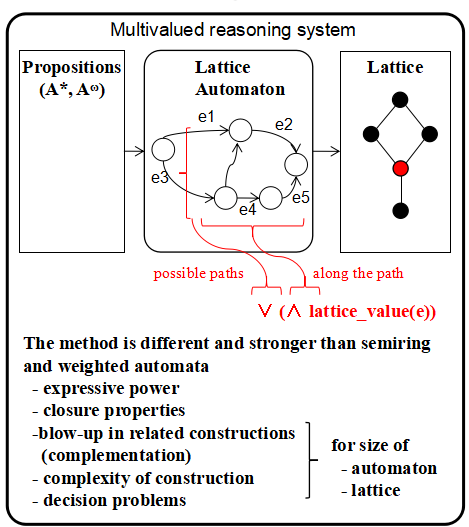
A∞ = A* ∪ Aω の文字列を命題と考えて,それを 入力として状態遷移を行い,命題の真偽値として束の値を割り当てるオートマトンです. Semiring あるいは重み付きオートマトンの方法より,図の下に書いてある性質についてより 強い結果が得られると書いてあります.
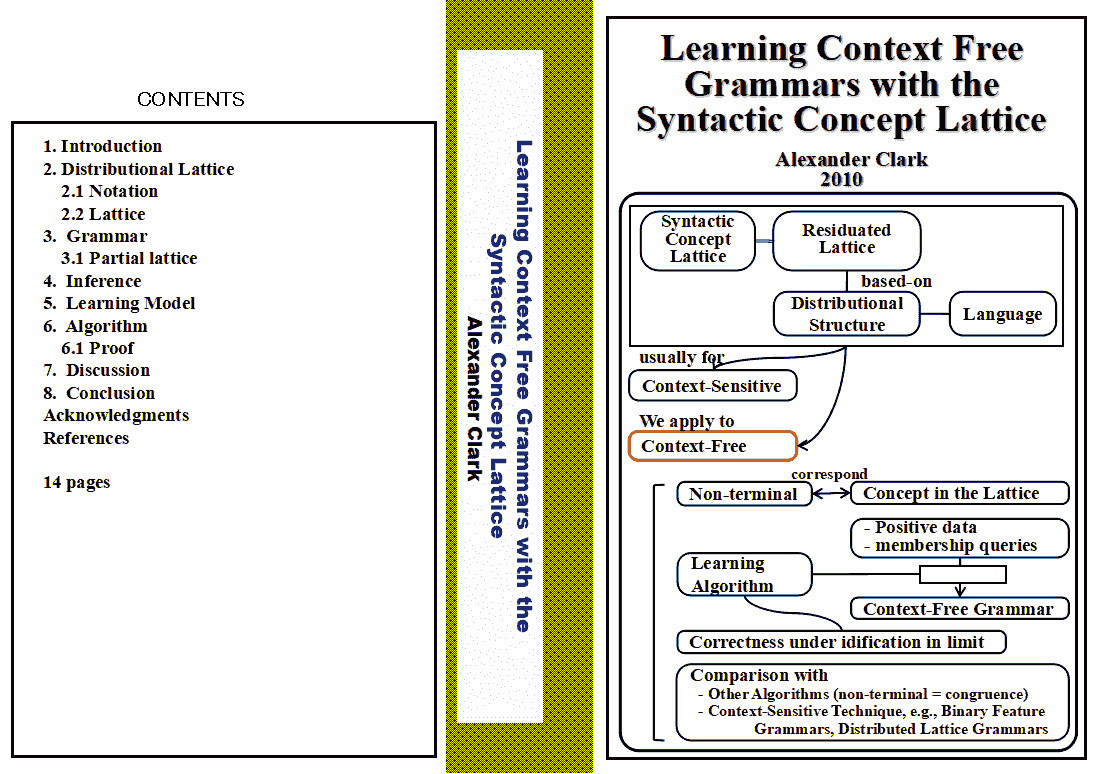
Syntactic Concept Lattice というのは形式言語の分配法則性に基づいた Residual Lattice のことです.通常,これは Context-sensitive な言語に関係しますが,この論文で著者らは これを図の下半分に書いてあるように言語の要素と対応付けて Context-free 言語に適用します.
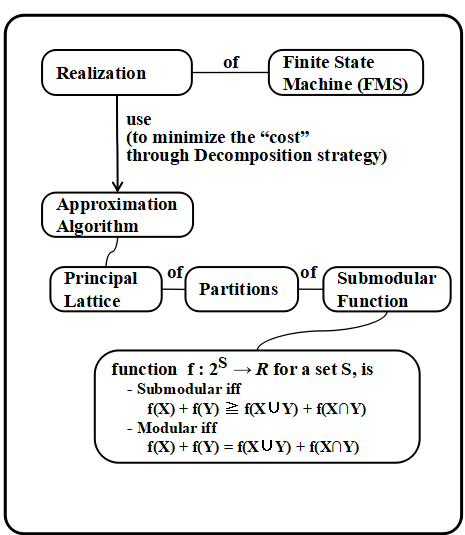
その他計算機への応用
基礎的な技術
上で出てきた residuated lattice のサーベイです.
Posets, Lattices の描画,生成,数え上げなど
束や順序集合を実際に目で見える形に表現したり,必要な束を次々に生成したり,いくつあるか数え上げる技術は計算機屋さんにとってはとても興味深く,重要なことですね.タイトルそのままですが.