ここでは，計算機科学に関連する順序集合(Posets : Partially Ordered Sets)の理論について，勉強したことや，思っていることを
書くつもりです．
タイトルの束論（Lattice Theory）というのは，象徴的に書いているだけで，
特に順序集合のうち，束論だけに特化するという意図はありません．本当は，順序を
弱めた Preorder にも多くの応用がありますので，このページの対象としては Preorder からです．
（一般のPosetsも含む）
ここでは，計算機科学に関連する順序集合(Posets : Partially Ordered Sets)の理論について，勉強したことや，思っていることを
書くつもりです．
タイトルの束論（Lattice Theory）というのは，象徴的に書いているだけで，
特に順序集合のうち，束論だけに特化するという意図はありません．本当は，順序を
弱めた Preorder にも多くの応用がありますので，このページの対象としては Preorder からです．
順序集合や束などに関する基本的な概念の説明に，順序集合と束論の基礎や，学習の TIPS 集のようなものを用意していますので，そちらを参照して， あとで暇が出来たときに「動機」から読んでいくという使い方もあります．）最近になって，束論の基礎をかなり拡充しました．
2021.03.10
ここでは，束(Lattice)，半束(Semilattice)，CPO (Complete Partial Ordered Set) , ガロア接続（Galois Connection）など，順序集合に関する 理論について，勉強したことや考えたことを書く予定です．
束論を勉強し始めると，
何のためにこの理論があるのか (PDF)，
考え込んでしまいます．応用が見えにくいのです．漠然と論理のモデルを作ったり，
物の関係を分析するのに使ったり（例えば，並列に動くプロセス間の依存関係の解析）には
使えるような気がするのですが，束論に現れる諸概念や定理がどのように使えるのか
ピンとこないのです．束論だけじゃなく，数学的な理論はみなその傾向がありますが，束論の場合は
特にそんな気がします．
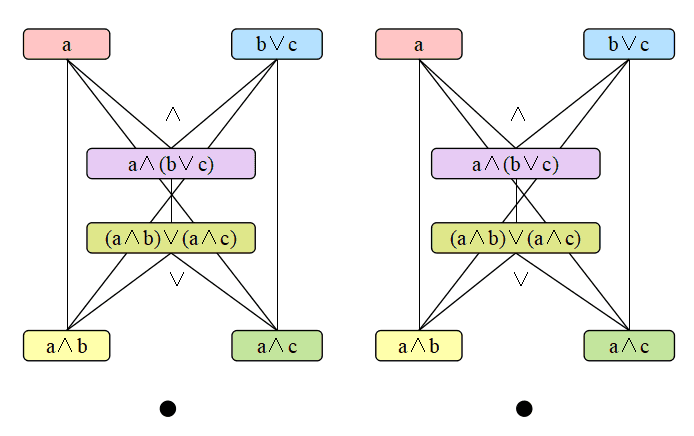
例えば，モジュラー束（modular lattice）という束が出てきて，色々な性質が証明され，それが分配束にも使えてと理論展開されるのですが，それがまた分かりにくいのです．
定義 束 (L, ≤) が（初心者には）定義もヘンテコに見えるし，第一，この不等式と等式に出てくる４つの 要素の大小関係が頭にイメージできない．紙に書いても分からない．実は紙に書くのも大変． 私は紙粘土と針金で立体モデルを作りました（これについては 障壁を引き下げるで，作成した 3D モデルのことなど，もう少し詳しく書いたモジュラー束 であるとは次の条件が成立することである．
c ≤ a ならば a ∧ (b ∨ c) = (a ∧ b) ∨ c ∀a, b, c ∈L
定理（第二同型定理） G を群，Nをその正規部分群，SをGの部分群とするとがすぐ導出できると言われても，「いやいや，ちょっと待て．NSub(G)がモジュラー束であることの 証明と第二同型定理の直接の証明とどっちが簡単よ？」って言いたくなります（あまり変わらないかな）．
(SN)/N ≅ S/(S∩N)
束論に限らず，一般に抽象数学の学習はかなり困難です．学習の効率を上げたり，学習をあきらめずに成し遂げさせるための基本的な方策は，
ここではこの三つの方策を少し詳しく見ていきましょう．ちなみに，「学習させる」と 他人に対してのような言い方をしていますが，ここでは学習者は自分自身も含みます．
私のような計算機科学に興味があるものにとっては，計算機科学への応用を見せるのが一番なんでしょうね．まあ，一応，すぐ見える応用としては，
などがあり，これだけでもずいぶんあるように見えます．でも，自分自身でさえ，そこまで 学習に乗り気がないし，世の中（特に日本）でも流行ってない．流行ってたら， 束論の本がもう少し出版されていて，学習環境が整っているはずです．各種形式論理のモデル, 形式的概念分析, 抽象解釈, 領域理論，...
認知的な負荷を下げるというのは有効だと思います．例えば，私はモジュラー束が
中々想像できなかったので，紙粘土と針金を使って立体モデルを作ったことがあります．
ホームページ上で見ることができるように
半順序集合に関する可視化の実験にステレオグラムを使った 3Dモデルを載せておきます．この3Dモデルを 何度も見てると，だんだん要素間の関係が分かってきて，条件式をイメージしやすくなる のではないかと思います（人によるかもしれませんが）． モジュラー束の条件式を出すための一連の認知的段差の少ないステップ列なども 概念になじむのに有効でしょう．これは束ではありませんが，半群のページで， グリーンの関係 のペーパークラフトを作成していたこともあります．これは，紙をハサミで切ったり， 折ったり，ノリでつけたりで，筋肉の動き，触感，ノリのにおいなど，五感に働きかけて 面白かったです．圏論の米田のレンマや随伴関手のペーパークラフトもこれらを イメージする気苦労を減少させてくれていると思います．
やはり，学習の動機を持たせてもらったり，障壁を引き下げてもらったりしても， 人任せでは学問は成就しません．複雑な概念を理解できるように， 自分自身が変わっていかねばなりません．私はあるところでＣ言語の応用編のような ものを教えていますが，分からないという学生をよく見てみると，その応用編が 分からないのではなく，その前から分かってないことが多いのです． 基礎的な概念を理解していなかったり，ごく簡単なプログラムの部分を解読するにも 随分悩んでしまい，肝心の応用編の新しい内容を読むのに振り向ける力が残って 無いのです．
そういう人たちは，遠回りに見えても，基礎編をもう一度やったり， ごくごく簡単なプログラムを何度も何度も書いてみると，今まで，超えられないと 思っていた障壁が，実は大したものではないということに気付くはずです． つまり，応用編を読むための，基礎編に関する十分な体力をつけるのです． でも，なかなか，後戻りしようという勇気は起きません．
振り返ってみて，自分たちはどうだろうと考えてみます．基礎が十分理解できているか？ 束論の教科書の最初の方の理解は十分か？ 練習問題はきちんとやったか？ 前の章は まったく苦痛なく読み返せるか？ 先ほど例に挙げたＣ言語応用編で挫折しかかっている 学生さんたちと同じことをやっていないかを考えてみて，もしそうなら，勇気を出して 基礎の理解，それも，あまり困難を感じなくなるまで何度もやり返してみるべきです．
これに有効な従来の方法は，証明を何度もやり直してみることみたいです．本に書いてある 証明を構造化したり，改良したり，本当に理解できるまでやってみると自然に力が ついてきます．
ただ，これは結構辛いです．これをある種，気軽にできるルーチンワーク的なものにする方法が あるのではないかと思い，目下，検討中です．これは日記の 計算機科学の発展を支える教育とは？ 2019 年 7月 11 日 (木) やどこが分からないのか分からない 2019 年 8月 22 日 (木) に書きました．ご興味があれば．
と言うことで，応用を挙げていき，それを整理していき，種々の把握しにくい概念の 視覚化や習得容易化を続けて行けば，学習者は増えるのではないでしょうか？ 実はこの類のことはイラストの練習の
ソフトウェア科学とボサツ様 (2017.7.19)にも書きました．
This side and that side in Software science
ソフトウェア科学とボサツ様のPDF版一応，圏論を勉強しよう( English Page "Let's Study Category Theory") も作成して，コンテンツを作成中です．
きっと，理論と応用が入り乱れていて，一度に整理しようとすると破綻するんだと思います． ここは，まず，最初のアプローチとして，Posets, Lattices (or Semilattices), CPO (Complete Partial Ordered Sets) と それらの応用の関係あたりを整理して，次第に理論と応用の地図を精密に描いていくのが 良いのではないかと思います．
例えば，次のような単純な絵を描いてみます．
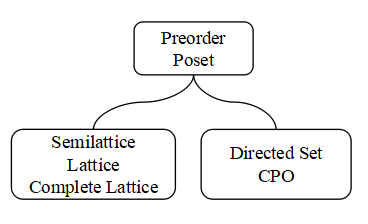
この絵に，思いつく応用や応用を目指した論文などを次々に付けていきます． きっと沢山の応用が付くような気がします． この単純な木では，それらの実は支えきれなくなるでしょう．そうしたら， 次第に形を整えて行けば良いのではないでしょうか？
ほんの少しだけ応用と思えるものを上げてみます．あまり粒度は考えていません．
順序集合や束論などの教科書や参考文献は次の項目で説明しているので，そこを 参考にして勉強するテキストを選んで欲しい．ここでは，それらを勉強するにあたって 知っておいた方がよいことや，勉強しながら参考になることなどを説明するつもりである． 具体的な内容は
順序集合や束などに関する基本的な概念の説明に書いた．束 (lattice) の定義についてや J.B. Nation のテキストでの Dilworth の定理の証明の 参考になる図，これまた J.B. Nation のテキストの 第３章 代数的束の概要などを書いている．今後も気が付いたものを書いていく 積りである (2018.01.14)．New (2018.01.14)
Wikipedia の Lattice (order) のページにも出てるくらい有名なので，皆さんご存知だと思います．
PDF は，いくつかのURLがあるようですが，著者自身のホームページ
J.B. Nation のホームページに最新のものがおいてあるようです．そこに置いてある Entirebook は，各章をまとめたものなのですが，必ずしも最新のものではなく，あるタイミングで各章のPDF を統合しているようなので 最新のものを確認したい場合は，各章の PDF を見てください．
私は，自家製の簡易製本で右の写真みたいな本にして読んでいます．ずいぶん前の
バージョンで前半後半別々のPDFだったときに製本していたものを１冊にまとめたため
このようなページ（もとは後半の表紙）が途中に挟まっています．キャラクターが結構かわいいでしょう．製本方法は
こちらに説明しましたので，ご興味の
あるかたは是非．この本の内容のことも書かないといけないので，製本についてはこれくらいにします．
内容としては標準的なことが書かれていると思います．
順序集合や束論がどのように応用に使われるかは，付録３にある形式的概念分析のこと以外は 書かれていません．
想定している読者のレベルはあまり定まっているようには思えません．大部分は大学の群論の基礎を 終えていれば（たぶん終えていなくても）読むことは可能とは思いますが，普遍代数の基礎は分かっている方が 良いと思います．普遍代数については，この本の付録にも申し訳程度のことが書かれていますが できれば，私のホームページの別ページで紹介している
A. J. Cain's "Nine Chapters on the Semigroup Art"の第８章 「Varieties & pseudovarieties」くらいの知識はあったほうが良いです． あるいは普遍代数についてはもう少し短いチュートリアルを こちらに紹介しました． たぶん，束論をやるときは普遍代数も併せて勉強した方が良いと思います． 理由は，通常の束論の本に，それらの理論構築の動機が書かれていないからです． 普遍代数は束論構築の一つの動機になっていると思います．
この本については，私は
J.B.Nation への要望に書きます． ２つ目は，第２章の
Comment on a set of closure rules in "notes on Lattice Theory by J.B. Nation" (English)一応，これも公開してよいと彼に許可を得ました．
この本は良い本だと思います．Cambridge University Press から出版されており， 有料で（少し値が張りま）すが，束論の基礎を学びたいなら，買っておいて損は ない本だと思います． 計算機科学などの応用のことについても触れてあります．また，ガロア接続を 使った形式的概念分析（FCA : Formal Concept Analysis）についても詳しく述べられています．
また， JON COHENという人が書いた秀逸なレビュー（PDF）によると，この本の著者は
「計算機科学者は〇ップレスモデルがお好き」という view を持っているそうです． ２ページ目の上から1/3くらいの Accordingly, computer scientists often choose ... のところです．これ意味分かりますでしょうか？ 実は，計算機科学でモデルとして使う順序集合はトップ（最大の要素）が無い順序集合が多いのです． これに対して，数学で，例えば，ある代数系のすべての部分代数のなす順序集合ではトップが あります．
These notes deal with an interconnecting web of mathematical techniques all of which deserve a place in the armoury of the well-educated computer scientist.と書いてあります．これは（だいぶ意訳になるかもしれませんが）
これらのノートは，教養のある計算機科学者（
well-educated computer scientists ）が （研究上の）武器として持っているべき数学的技術がWebのように相互に結合されたものに 関するものである．
内容は以下のようなものです．
B. A. Davey &H. A. Priestley の教科書のJON COHENによるレビューで
..., and topless models are often to be preferred.と書いてありますね．Hilary さん，女性の方なんですけどね．
これはまだ読んでいませんが，私の積読（つんどく）リストに入っているので，ここにものせておきます．
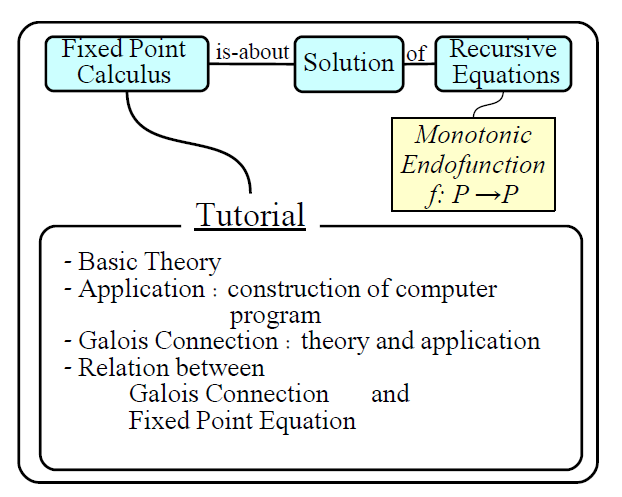
このチュートリアルはガロア接続と不動点計算のチュートリアルです（それじゃあ，タイトルのまんまでんな）．
概要（abstract）によるとガロア接続の基本的な理論と，応用として計算機プログラムの構成を
扱うらしいです（右の図のような感じ）．
目次を章レベルで載せておきます．
まずは本棚から次々にリストしていくだけなのであまり分類していないかも
しれませんが，主に，
Poset, Lattice 関係で読もうと思っている文献リスト
（ちょっと個人の覚書のような内容で申し訳ありません．次第に整理していきます． 圏論の方はここより整理ができていますので，ご興味のある方は
圏論 (Category Theory) のお勉強もご参照ください． ）
ホームページトップ(Top of My Homepage)
