J.B. Nation のホームページ
(ここで "Notes on Lattice Theory" を見つけてください)
束論に関しては，
注意：このページに書いてあることは，もしかしたら私の勘違いを含んでいるかも しれませんので，あくまで参考にするという目的で，最終的には皆さん自身の 頭で判断してください．
少し再構成を始めました．このページは，もともと，J.B. Nation 教授の束論の教科書を読むのに， 気を付けることを散発的に書いていたのですが，今， 前半部分に順序集合や束論の基礎をかなりの分量補充していっています．
順序集合の基本概念についてある程度の数の解説を加え，再構成しました．
x < y ならば ¬ (y < x)
記法としては y≤x のことを
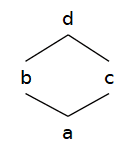
一応，例と図による表現方法を示しておきます．
この図は
ハッセ図では対象関係は矢印でない普通の線と図上の上下関係を使って，元の大小関係を 表しますが，圏論などでは，小さい方から大きい方へ矢印を書くことがあります． ここでも，特に大小関係で方向を表現する必要があるときはこのように書くことがあります．
ここでは，順序集合の例をもうの少しだけあげておきます． 後で，もう少し沢山上げると思いますが，ここでは順序集合をイメージするのに 最小限の例をあげるに留めます．
この順序集合の元は 0 と 1 と書きましたが，名前は本質的ではないので false, true と読み替えると，真偽値を表す順序集合とも思えます．
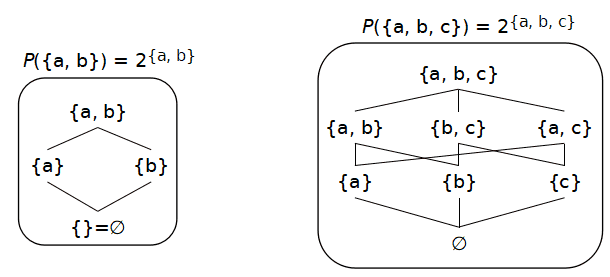
この順序集合は便利で，どんな順序集合も，ある集合の冪集合の中に埋め込むことができます．「埋め込む」というのは 同型写像を定義しないと正確に述べられませんが，埋め込み先の順序集合の一部の元を取ってきて， そこの順序で埋め込まれる元の順序集合が表現できることだと思ってください．
を満たすときは，(P, ≤) は
例えば，次の図のようなものが前順序集合です．ここではハッセ図と違って， 小さな元から大きな元へ矢印を引いています．例えば， 元 a と c はお互いに相手より大きいので図上の上下関係だけで大小を表現できないのです．
(P, ≤) が前順序集合のときは，P 上の同値関係 ～ を
x ～ y iff x ≤ y ∧ y ≤ xiff は if and only if の略．
つまり A iff B は，AとBが同値という意味です．
で定義すると (P/～, ≤') は順序集合になります．ただし，P/～ は， P の～による商空間を表します．つまり， P の中で，～の関係にある元を１つの元に纏めたもので，x が纏められた新たな元を [x] と表します．そして，[x] と [y] の大小関係を次のように定義します．
[x] ≤' [y] iff x ≤ y
例えば，上で上げた前順序集合の例からこの方法で順序集合を 作った様子を図に示します．左の図の中で赤の点線で囲った元の集合を 右では１つの元と思うことで順序集合になる訳です．
これらの概念は非常に重要なので自分で絵に描いたりしてしっかり身につけて ください．一応，定義を書いておきます．
(P, ≤) を順序集合とします．
P の部分集合 A⊆P についても，P の順序で (A, ≤) に最小元があれば，
それをAの最小元と言い，
二つほど，特殊な場合を絵にしておきます．
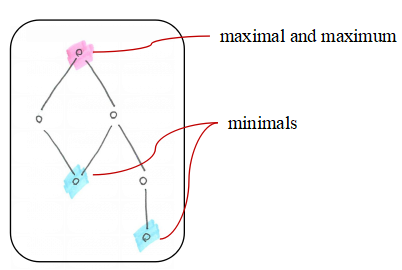
「極大元 (maximal) が１個のとき最大」という記述を見たことがありますが，それは
ウソです．
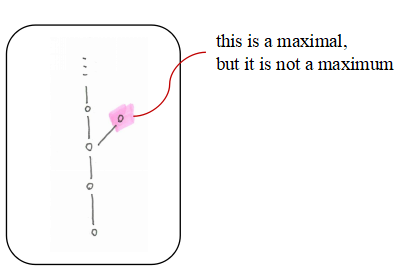
次の poset は唯一の極大元を持つが最大元は持ちません．ただ，有界な順序集合で
で極大元が１個ならそれが最大元ですね．
The following poset have a unique maximal, but no maximum.
∀ x, y∈P (x ≤ y ∨ y ≤ x)
チェインとは逆にまったく他の元と比較できない順序集合を
この資料の後の方で Dilworth の定理が出てきますが，鎖と反鎖はそこで使います．
[a, b] := {x∈P | a≤x かつ x≤b}と書きます．このように，[a, b] と書くと実数の区間のアナロジーで， 一直線に並んでいる値の集合のように思えるかもしれませんが，(P, ≤) の 構造次第で，途中に枝分かれや合流があっても構いません．
補足：Sd は，J.B. Nation の教科書では Sl （S の肩に lower を表す小文字の L）となっています．これは筆記体だとはっきり L の小文字 だと分かって良いのですが， 活字体だと，小さいので 1 (数字) と間違えやすいと思いましたので，ここでは， down の d を使うことにしました．
いま，(P, ≤) を順序集合として，A⊆P とします．
∀y∈A (y≤x)集合 A のすべての上界の集合が，上で導入した Au ですね．
上界の集合の中に，最小元がある場合は，それを
集合 A に最大元 max A が存在した場合は，上限 sup A はそれと一致します． したがって，sup A が A に属する場合もあります．
いくつか例にあたっておいたほうが良いかもしれません．
まず，有限集合の上界と上限です．以前イデアルなどの説明に使った順序集合を 再利用します．次の図で，集合 A = {e, f, g} とすると，A の上界は，b, a です． それらはすべて，A のすべての元以上の元です．その上界の集合 {a, b} には 最小限 b がありますから，sup {e, f, g} = b です．
次は B={f, g} の場合を考えてみます．f と g 以上の元を列挙すると b, c, a です． この中で b と c は比較できませんから，最小元は存在しません．b と c はそれぞれ，集合 B の上界の極小元ではあるのですが，残念ながら最小元ではないのです．したがって，B の上限は存在しません．一般に次の図のように比較不能な直上の元が２つ以上あると上限は存在しないのです．皆さんも，仲の悪いどちらが偉いか分からない上司が二人いると苦労するでしょう．
では，{g} の上限はどうでしょう？ b と c が g の上界でそれらが比較できないので， 一見，上限に最小元が存在しないと思うかもしれませんが，実は g 自身も g の上界 で，これは b や c より小さいので，これが上界の最小元になります．したがって， これが上限です．このように１個の集合には常に上限がその元そのものとして存在します．
次は無限集合の場合も見ておきましょう．次の図に３つの無限集合である順序集合を 示します．P1 は自然数の集合に通常の大小関係を入れたものです．P2 はその上にもう一度 自然数をω+なんとかという形で積み上げたものです．P3 は自然数の上に無限集合を 積むのですが，それはさかさまに積んで，それらはすべて最初の自然数より大きいと します．つまりここには無限降下列がある訳です．
P2 では，A={0, 1, 2, 3, ...} の上に ω, ω+1, ω+2, ... という元が 存在し，それらは A の上界になります．そして，それらの中で一番小さい元 ω が A の上限になるわけです．P3 は同じように，A={0, 1, 2, 3, ...} の上に無限個の 元を置いてあるので，それらが，A の上界になります．しかし，P3 の場合は A の上の 部分は下に無限の降下列がありますから，それらの最小元は存在しません．従って， A の上限は存在しない訳です．
∀y∈A (y≥x)上界のときと同様に，集合 A のすべての下界の集合が上で導入した Ad です．
A の下界の集合に最大元があるときは，それをA の
最後に１つ注意ですが，順序集合 P に置ける，空集合 ∅ の上界，上限， 下界，下限はどうなるでしょう．まず，上界ですが，この上界は ∅ の中の元 y に対して それ以上になる元です．∅ には元は存在しませんから，仮定が偽になり，すべての 元が ∅ の上界になります．したがって，∅ の上限は，P の最小元です． 最小元が存在しないときは，上限は存在しません．同様に ∅ の下界もすべての 元であり，下限は P の最大元です．これらはあまり納得しにくいかも知れませんが， その場合は，決まり事だと思ってください．式としても書いておきます．
上の式を見ると，左辺には P が現れずに右辺だけに P が現れています．変ですね． だから sup や inf は，順序集合 P に置ける sup や inf という概念なので， 本来は supP や infP のように，P が示されるべきなの ですが，面倒なので省略してあるだけですね．sup ∅ = min P
inf ∅ = max P
二つの元 a, b∈P に対して，{a, b} の上限を
任意の２元を繰り返すと，束では任意の（空集合以外の）
有限集合に対して上限と下限が存在します．上限と下限の両方の存在を要求するのではなく，
上限だけ，あるいは下限だけの存在を要求した順序集合を
∀x, y∈P (x≤y ならば h(x)≤h(y))
準同型写像のことを
(P, ≤) と (Q, ≤) が
ここで注意しなければならないのは，h : P → Q なる１対１全射の準同型が存在する だけでは，同型には不十分であるということです．群などいくつかの場合に，１対１全射の準同型写像は自動的に同型写像になることがありますが，順序集合の場合はそうはなりません． それは例えば次の図のようなものを考えてみればよいと思います．h は準同型ですが， h-1は準同型ではありません．
もう一つ，重要な概念として
埋め込み e : P &rarr: Q は，Q の性質が良く分かっているとき，その知識を P の
解析に利用したり，あるいは，Q が大変良い性質を持っているとき，P を Q に
拡張して利用するといった使い方があります．例えば，有理数の集合 Q は
そのまま実数の集合 Rに埋め込まれますが，実数の集合は任意の有界な
上昇列が実数の中に収束するなどの良い性質を持っています．
上で準同型を学んだのでそれを使ってみます．今，二つの順序集合
(P, ≤) と(Q, ≤) および，準同型 h : P → Q があったとします．
q∈Q が Q の中の極大元とするとき，F := h-1(q)⊆P は
順序集合 P の中のどんな集合でしょう？
F はフィルターになります．なぜなら，
したがって，h(y) = q となり，
同様に Q の極小元の h の逆像はイデアルになります．
では，フィルターは必ず何か準同型の極大元の逆像になるでしょうか？
答えは yes です．以下にそれを示します．
(P, ≤) を順序集合，F⊆P をフィルターとするとき，フィルターの元を
１つの元と見ることにより，順序集合 (P', ≤') を作ることができます．
これが順序集合になるのは，順序集合の３つの条件を調べる
必要がありますが，ここでは省略します．
ここで，写像 h : P → P' を
イデアルの方も上下をさかさまにすると，１つの元に纏めた，もとの
順序集合と準同型な順序集合を作ることができます．
以前，示したフィルターとイデアルの例を一つにまとめた順序集合を例と
して，次の図に示します．
このようにしてイデアルとフィルターを１つの元に写す時，それぞれの
写される先の元は極小元と極大元になります．
ということで，イデアルとフィルターは何かの準同型で，ある順序集合の
極小元と極大元に写されるもとの元の集合な訳です．
ここで言う
ここで述べた，
ただし，束の場合もある程度条件をつければ，これが成立することもあります．
この表現方法というのは，次のようにして，順序集合 P を P の
部分集合の集合 2P=P(P) に埋め込む方法です．
r(x) := ↓x = {y∈P | y≤x}
(2P, ⊆) が順序集合になるのは以前説明しました．つまり，この順序集合の中に，P と同じ構造の
順序集合を作ることができるということです．
ちょっと具体例に触れておきましょう．例えば，以前に例として示した順序集合
r(c) = {c, f, g, j}
という集合で表すことができます．同様に全部の表現を列挙すると
r(g) = {g, j} ⊆ {b, e, f, g, j} = r(b)
から，b の方が大きいことが分かり，r(b) と r(c) の比較では，これらの
間に包含関係がないことから，比較はできないことが分かります．
これは計算機で順序集合を表現するとき威力を発揮します．グラフ構造を
そのまま持つと，大小関係はリンクを辿って，どちらかから他方へ到達できるか
どうかを調べなければなりませんが，一般にこれは計算量が大きいのです．
それに対して，集合の包含関係のチェックはそれほど大きくはありません．
特に，元の数が 32個以下の場合は，元の並べ方を決めておいて，ある元が
入っているかどうかは整数のその位置のビットを立てるという表現方法を
とれば，x で表現される元が y で表現される元より小さいことは，
x と y のビットごとの OR = x
で調べることができます．例えば，上の例で，a, b, c, ... を２進数の下の桁（右側）から，1ビット目，2ビット目，3ビット目と割り当てていくと，
r(e) = {e, j} ですから 0b1000010000 = 528
r(g) = {g, j} ですから 0b1001000000 = 576
c と g はビットごとの OR をとると 612 | 576 = 612 であるから c が大きい
c と e は 612 | 528 = 628 となり，比較できない
また，順序集合 P にもう少し条件が加わる場合，例えば，
後で述べる束（lattice）になるような場合は，x を↓x で表現する
のではなく，その中のある基準で重要な要素
（irreducible elements）だけに限ることも
できます．
そうすると，計算機での表現ではより少ないメモリーで元を表現することが
できます．
e: P → Q が
イデアルとかフィルターって，定義は一応分かるのだけど，なんでこんな概念を
定めるのという疑問を持ちやすい概念だと思います．特に，後で述べるかもしれない束の文脈でのイデアル，フィルターはこれらにさらに条件が加わって不思議な感じがします．ここでは，イデアルとかフィルターって何だろうという疑問をちょっとだけ考えてみます．
x∈F=h-1(q) かつ y ≥ x ならば
h(y) ≥ h(x) = q ですが，q は極大ですから，q より真に大きな元は
ありません．
P' := P - F + {*} ここで * は，P の中に現れない元
x, y∈P' に対する順序 ≤' は次のように定める
h(x) = * if x∈F
で定めると，h は準同型写像になります．
h(x) = x otherwise
2021.02.12 (金) 追加
2022.02.18 (金)
(P, ≤) を順序集合とします．これはサイクル（巡回路）の無い
グラフ（頂点と向きのあるエッジからなるもの）なのですが，
P のそれぞれの要素を集合として表す簡単な方法があります．これは
順序集合の解析や，あるいは，計算機の中での効率的な大小関係の判定に
有効な手段を与えます．ここではその表現方法を紹介します．
r : P → 2P
P ≃ r(P)⊆2P
という訳です．同じことを繰り返しているような気もしますが，
さらに強調して言うと，どんな順序集合もある集合の部分集合の作る
順序集合の中に埋め込むことができることを意味しています．
で，それぞれの元がどのように表現できるか実際に計算してみましょう．
例えば，r(c) は c 以下の元が，c, f, g, j ですから，
r(a) = {a, b, c, d, e, f, g, h, i, j}
となります．この表現の良いところは，大小関係の比較が包含関係の
比較でできるところです．例えば，b と g のどちらが大きいかを比べるためには
r(b) = {b, e, f, g, j}
r(c) = {c, f, g, j}
r(d) = {d, h, i, j}
r(e) = {e, j}
r(f) = {f, j}
r(g) = {g, j}
r(h) = {h, i, j}
r(i) = {i, j}
r(j) = {j}
r(c) = {c,f,g, j} ですから 0b1001100100 = 612
というような計算ができます．最近は 64ビットの計算機が主流ですから，
この手法は 64 個以下の元からなる順序集合で用いることができます．
勿論，配列を使えばもっと多くの元の順序集合でもこの方法は使えます．
2021.02.13 (土) 追加
ACC : ascending chain condition
集合 A と B に対して，
次に PFun(A, B) に順序を次のように入れます．
f, g ∈ PFun(A, B) に対して，f≤g iff dom(f)⊆dom(g) かつ f(x) = g(x) for ∀x∈dom(f)
つまり，f の定義領域が g の定義領域に含まれていて，f の定義領域内では f と g が一致するという条件です．言い換えれば，部分関数 g が 部分関数 f の拡張になっているときに f≤g とする訳です．
なぜ，この順序集合が計算機屋さんにとって重要かというと，プログラムの意味を 定めるときに，こういう領域を使って最初は ⊥ つまり，A のどこでも未定義な 部分関数からはじめて，次第に色々なところで定義される部分関数として，プログラムの 意味を近似していくといったことができるからです．これについてはそのうち 書くかもしれません．
つまり，A の有限部分集合で定義されている部分関数の集合です．A が有限集合なら， PFunfin(A, B) は，PFun(A, B) に一致しますが，A が無限集合なら一致しません．また，A が無限集合の場合は，PFunfin(A, B) の中に（全域）関数は 入っていません．このため，上限が存在しない X⊆PFunfin(A, B) が 色々と発生してしまいます．PFunfin(A, B) := {f∈PFun(A, B) | dom(f)が有限集合}
int factorial(int n) {
if (n == 0)
return 1;
else
return n*factorial(n-1);
}
こういう文字列にそれが意図する数学上の関数を対応させる理論がプログラムの
意味論です（C言語など所謂，副作用のある言語は意味を与えるのは難しいので
上の例は適切な例ではないかもしれませんが，ここでは意味論って何かを説明するのに
よく知られているC言語の例を出しました）．
こういうプログラムの意味を定めるのに，この文字列に整数から整数への関数を 対応付けるという方法があります．そのとき，一気にそのような関数を定めることが 難しくて，上の例でしたら，最初は全整数領域で未定な関数，次は 0 に対して 1 を 返す関数，さらに，1 に対しても 1 を返し，次は 2 に対しては 2 を返す関数，．．． と次第に色々な引数に対して値を決めていき，その極限を，与えられたプログラムの 意味とする手法があります．
ここまで長々と動機を説明してきましたが，
順序集合 (D⊥, ≤) D⊥ は D ∪ {⊥} とする．
D⊥ 上の順序は次のように定める．
⊥ ≤ x for ∀x∈D ∪ {⊥}
要は，D に新しい要素 ⊥ を加えて， D のすべての要素の下に ⊥ を 置くというだけです．⊥ は，ボトム (bottom) と読み，直感的には「不定」を表します．
このように定義すると前に定義した部分関数の順序集合 PFun(A, B) は，A から B⊥ への関数の集合 (A→B) に順序
f≤g iff f(x)≤g(x) for ∀x∈Aを入れた順序集合 ((A→B), ≤) と考えることができます．A に ⊥ を 入れると，この集合とはちょっとだけずれますが，面倒なので，全部の集合を 平坦領域にしておくと部分関数を明示的に扱わなくとも済みます．
順序集合 (W, ≤) が
∀D⊆W ∃ min(D)∈D⊆W
ということです． 整列集合 W に対しては，x, y∈W のときは {x, y}⊆W ですから，最小元があります．x か y のどちらかが最小元になる訳 ですね．したがって，整列集合では 任意の２元が比較可能ということになり，必然的に全順序集合になります．
整列集合は数学的帰納法（超限帰納法）の基礎となる集合で重要です．さらに詳しい説明は 集合論のページに ありますので，ご存じない人は勉強しておいて下さい．ただし，このページの 内容を読むためには必須ではありません．
順序集合での極大元の存在に関する重要な命題である
ただし，このページを読むのに，Zorn の補題はそれほどは必要なく，
ざっとどんな補題で何に使えるのかを知って入れば当面は問題ないと
思います．
束やその条件を少し緩めた半束は，順序集合としても，代数系としても特徴づけることができます． ここではまず，順序集合として特徴づけて，この項目の最後で半束の代数系としての 特徴づけ，次の項目で束の代数系として特徴づけを紹介します．順序集合としての 特徴づけと代数系としての特徴づけは同値になります．
束を定義するのにまず，その約半分の公理を満たす半束（semilattice）を定義します． 半束は上への半束と下への半束があります．それら両方を満たすのが束（lattice）です． ここでは，このようにして束を定義した後，そのような束で極限操作について特に 良い性質を持っている完備束（complete lattice）について定義しておきます．
この公理を論理式で書くと
∀x,y∈S ∃(x∨y)∈Sです．本当は x ∨ y の定義もこの式に入れないといけないような気はしますが， これはどこかで定義されているということにしておきましょう．
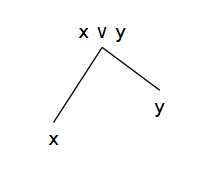
上では二つの元の上限を定義通り，上界の最小元として図示しましたが， 普段は簡単に次のような図を思い浮かべて良いと思います．
次に，下半束（meet-semilattice）ですが，これは上半束の上下逆のものです．
順序集合 (S, ≤) が上半束と下半束を，上下をあまり区別しないで良い文脈で言う時には，簡単に下半束（meet-semilattice） であると いうのは，S の任意の２つの元 x, y に対して，それらの下限 x ∧ y が 存在することを言う．
以下，ちょっと半束の性質を見ておきます．
(S, ≤) が上半束ならば任意の x, y∈S に対して，それらの上限 x ∨ y が
存在しますが，これは
∨ {x, y, z} = (x ∨ y) ∨ zとすれば良いからです．こうして良いということを言うためには，２つの元ごとの 上限を取る順番をどのようにしても同じになることが必要です．つまり，
x ∨ y = y ∨ xが言えている必要があります．上の等式は，x ∨ y は，x と y の上限，つまり， x 以上かつ y以上の元の中の最小元ですからわかると思います．二つ目の等式は 式で証明することも出来ますが，絵を描いて納得しても良いかと思います．(x ∨ y) ∨ z = x ∨ (y ∨ z)
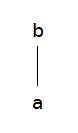
これらだけでなく，全順序集合は半束です．
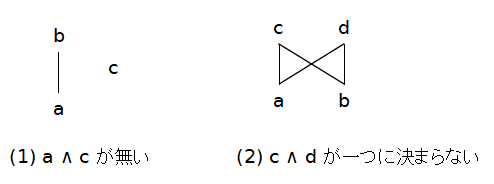
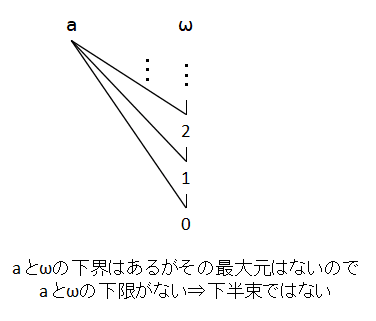
もう一つ，下半束にならないものをあげておきます．次の図は，自然数の集合に ωと a という元を加えて，自然数の間には通常の順序を入れ，ωと a はその上に 置きます．また，ωと a は順序関係はないものとします．
f(x∨y) = f(x)∨f(y) for ∀x, y∈S
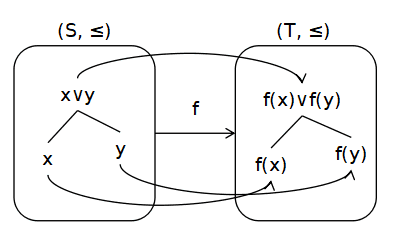
x≤y ならば x∨y=y ですから f(x∨y) = f(x)∨f(y) = f(y)となり，f(x) ≤ f(y) が言えるからです．
また，
下半束についても準同型は同様に定義されます．
a ∨ b := max(a, b)で，上限と下限が与えられますから，(P, ≤) は束です． 例えば，自然数の集合，整数の集合，実数の集合は，それらの普通の順序で 束になります．a ∧ b := min(a, b)
A ∨ B := A ∪ BA ∧ B := A ∩ B
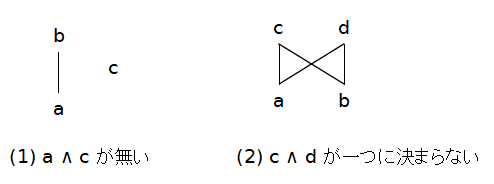
すでに，このページの前の方のイデアル（order ideal, lower set）とフィルター（order filter, upper set）で，順序集合における order ideal と order filter を 述べました．そこでは order ideal は下に閉じた集合，order filter は上に閉じた集合 でした．
実は，束論では，束の文脈でもイデアルとフィルターがあります．むしろ，単に イデアルやフィルターと言った場合，束のイデアルやフィルターを指すことが多いです． ここでは，それら束のイデアルとフィルターについて説明しておきます．
(L, ≤) を束とします．束ですから，任意の２元 x, y∈L に対して， 上限 x∨y と下限 x∧y があります．
L の部分集合 I⊆L が
さらに空集合でないという条件を付けることもあります．
この向きを反対にしたのがフィルターです．
F⊆L が
こちらも空集合でないという条件をつけることもあります．
order ideal や order filter と違うのは，それぞれの条件で 2 の条件が追加されている ことです．
修正（2022.03.18）：以前，ここにはさらに以下の記述がありましたが， これは私の勘違いでした．束のフィルターは必ずしも，準同型の逆像（なんらかの元の逆像）にはなりません．
以下の取り消し線の部分は間違い以前の，order ideal や order filter は，何らかの順序に関する準同型で 新たな順序集合の極小元，極大元に写されるもとの順序集合の中の部分集合でした．
束におけるイデアルやフィルターは同様に束における準同型で，新たな束の中の 極小元や極大元に写される元の束の部分集合です．（特に2={0, 1} への準同型 φ における 1 の逆像はフィルターになります． これについて，将来もしかしたら補足を書くかもしれません）
束のフィルターが束の準同型の最大元の逆像にはならない例を書いておきます．
しかし，この例も，次の図のように順序集合の準同型の逆像にはなっています．
∀A⊆L ∃∨A∈L かつ ∃∧A∈L
完備束が普通の束と違うのは，A が無限集合でも良いところです．A が有限集合なら 上で半束のところで書いたように，普通の束でも A の上限と下限は存在します．
ところで，実は，任意の上限が存在すれば，A⊆L の下限は
∧ A = ∨ (L - A)ですから，存在することが分かります．したがって，「完備束とは，任意の部分集合に対して その上限が存在する順序集合である」と言っても構いません．また，当然上限と下限を 入れ替えても同じことが言えますから，「完備束とは，任意の部分集合に対して その下限が存在する順序集合である」と言っても構いません．
x, y∈L に対して，{x, y}⊆L で，当然，x∨y と x∧y は 存在しますから，完備束は束でもあります．
f : L → L が次の条件を満たす時，f を
f(∨ A) = ∨ f(A)f(∧ A) = ∧ f(A)
ただし f(A) = {f(a) | a∈A}
完備束を定義したので
(S, ≤) を上半束が，その任意の部分集合 A⊆S に対して，上限 ∨ A が存在する
ならば，(S, ≤) を
同様に，(S, ≤) お下半束とするとき，その任意の部分集合 A に対して，下限
∧ A が存在するなら，(S, ≤) を
(S, ≤) が完備上半束のときは，A⊆S に対して，下限 ∧ A を
∧ A := ∨ Adで定義することができますから，実は
です．(S, ≤)が完備束 ≡(S, ≤)が完備上半束 ≡(S, ≤)が完備下半束
⊤ = ∨ L⊥ = ∧ L
これについては，Knaster-Tarski の不動点定理に詳しく書きましたので，そちらをみて下さい．∨ {x∈L | x≤f(x)} （最大不動点）
∧ {x∈L | f(x)≤x} （最小不動点）
∨ A = ∪ A∧ A = ∩ A
∨ A = ∪ A
で完備上半束になります．しかし，開集合系は交わりに関して閉じて いませんので，冪集合と同じ式では下限は求められません． しかし，上の完備半束のところで説明したように，下限を
∧ A = ∨ Ad = ∪ {Z∈OX | Z⊆Y for ∀Y∈A}で，与えることができます． 開集合は無限個の和集合をとっても開集合ですからこの式は A に含まれるどんな開集合以下の最大の開集合になります．
例えば，実数の集合 R の開集合の集合 OR に おける開区間の集合
{(0-a, 1+a) | 0 < a < 1}
を A とすると，
∧ A = (0, 1)になります．これは Rの冪集合で下限を取ると，閉区間 [0, 1] になりますから，どの束で下限をとるかで結果に違いがでてきています．
∨ A = max Ac∧ A = min Ac
Ac は A を含む最小の閉集合とする
x∈I かつ y∈P が y≤x ならば y∈Pつまり下方に閉じている P の部分集合です．P のイデアルすべての集合を
A⊆O(P) ならとなるからです．∨A = ∪A ∈ O(P)
∧A = ∩A ∈O(P)
これがなぜ重要かと言いますと，写像
r : P → O(P)で，順序集合 (P, ≤) を完備束 (O(P), ⊆) に埋め込むことができるからです．x∈P と↓x∈O(P) を同一視すれば，順序集合 P が完備束 になるのに足りない元を補って，完備束になる一つの方法を与えることになります．r(x) := ↓x
{q∈Q | q2≤2}
の上限は，√2 であり，有理数ではありません．こういう上限の
無いところに数を補ってできたのが，実数の集合 R な訳です．
皆さんはここで補う方法として
実は，上で述べた (Q, ≤) のイデアルの集合(O(Q), ⊆) は デデキントの切断と本質的に同じ方法で，P に元を補って完備束 R つまり実数の集合と同型の順序集合を作っていることになります．
・∨・ : S × S → Sが定義されているとも考えられます．上限は次の３つの性質を持っています．
実は，集合 S の上に定義されている二項演算 ∨ がこれらの性質を満たす時， S の上にある順序 ≤∨ を
によって定義することができて，その順序で (S, ≤∨) は 上半束になり，x, y∈S の上限は x ∨ y と一致します．一応，これを 証明しておきましょう．x ≤∨ y iff x ∨ y = y for x,y∈S
x ∨ z = x ∨ (y ∨ z) = (x ∨ y) ∨ z = y ∨ z = z
となり，x ≤∨z が分かります．
x ∨ (x ∨ y) = (x ∨ x) ∨ y = x ∨ y ですから以上で，x ∨ y は，x と y の上限になることが分かります．x ≤∨ x ∨ y
y ∨ (x ∨ y) = (x ∨ y) ∨ y = x ∨ (y ∨ y) = x ∨ y ですから
y ≤∨ x ∨ y
したがって，x ∨ y は x と y の上界です． 次に，これが最小の上界であることを言います．
いま，z を x と y の上界であるとし，x ∨ y ≤∨ z であることを言います．
(x ∨ y) ∨ z = x ∨ (y ∨ y) = x ∨ z = z
となり，(x ∨ y) ≤∨ z が分かります．
x ∨ y は，x と y のどんな上界 z に対しても x ∨ y ≤∨ z ですから，上界の最小元となります．
ここでは上半束を代数として定義する方法を述べましたが，同様に 下半束も代数として定義することができます．
束(lattice)の定義は次のようないくつかの公理からなっていると思う．
これを初めて見た学習者は，なんだかゴチャっとした公理があって，何を言っているのか 分かりにくいと思う．
これは次の図のようなことを言っている．
まず，(1) - (3) は 半束の代数系による定義 で述べたように ∧ と ∨ が それぞれ順序 ≤ ∧ と ≥ ∨ を定義し，それぞれが 半束 (semilattice) であることを言っている． (4) は，Absorption law と呼ばれ，上のようにして定義した二つの順序 ≤ ∧ と ≥ ∨ が同じ順序であることを言っている．つまり， (4) の条件の元には
(4') x ≤ ∧ y <=> x ≥ ∨ yであるし，その逆に(4') が成り立てば，(4) が成り立つことが証明できる． (1)-(3) と (4) をまとめると，一つの順序 ≤ ∧ (つまり， ≥ ∨) について，x と y の上限と下限があることを言っている訳である．
ちなみに，<L, ∧> が半束である条件は次のような名前がついている．
3 の結合性は群論などで良く知られているだろう．二項演算が定義されている 集合は，これが成立すれば半群 (semigroup) と呼ばれる．
1 の冪等性はあまり面白くない性質のように思うかもしれないが重要な性質で， 半群や位相空間の理論で大活躍する性質である．例えば，群やモノイドの単位元 e は この性質
e・e = eを持つ代表的な元である．半群論では，部分に限れば群構造を 持つ部分を見つけることができる場合があり，そのときの単位元の候補でもある．
2 の可換性もよく使う性質で，群論の基礎を勉強した学習者はアーベル群の定義などで 馴染みのある性質だと思う．この性質があると代数系の構造がかなり簡単になる．例えば， 有限生成のアーベル群は巡回群の直積に分解できることは良く知られている．
条件 1 の冪等性 (idempotency) と条件3の結合性 (associativity) を併せて持つ代数系を帯 (band) と言うので， 半束 (semilattice) は可換帯 (commutative band)である．
(L, ≤) を完備束，f : L → L を順序保存写像とするとき， L には f の不動点，つまり， f(x) = x となる元 x が存在する．
さらに，それらの不動点のうち，最大不動点と最小不動点は次の式で与えられる．
最大不動点
∨ {x∈L | x≤f(x)} 最小不動点
∧ {x∈L | f(x)≤x}
まず，u :=[証明終]∧ {x∈L | f(x)≤x} として，u が不動点であることを証明する．任意の x∈{x∈L | f(x)≤x} に対して，u≤xであり，f は順序を保つので，
f(u)≤f(x)≤x
となり，f(u) は{x∈L | f(x)≤x}の下界の１つである．u はそのような下界の中の 最大元であるから
f(u)≤u ........ (1) f は順序を保つので
f(f(u))≤f(u)
となり，
f(u)∈{x∈L | f(x)≤x}
u はこの右辺の下限であり，したがって下界でもあるから，
u≤f(u) ........ (2) (1) と (2) から u=f(u) となり，u は f の不動点になる．
次に u が最小不動点であることを示す．f の不動点の集合を Fix(f) とすると，
Fix(f)⊆{x∈L | f(x)≤x}
したがって，u は Fix(f) の下界でもあり，最小元となる．
次に，
∨ {x∈L | x≤f(x)} が f の最大不動点であることで あるが，これは 上の議論の上下を逆さまにすれば分かる．
この定理から，完備束 (L, ≤) では順序を保つ関数 f : L → L に対して， 必ず，不動点，つまり f(x) = x となる x があることが分かります．それは， {x∈L | x ≤ f(x)} の上限をとったりすることで見つかるはずですが， 無限個の要素を持つ領域ではなかなかこれはできません．もう少し簡単に
⊥ f(⊥), f(f(⊥)), f(f(f(⊥))), ..., fn(⊥), ...
と言った具合に段々近似していくというアイデアもあると思います．残念ながら， これが常に可能とは限りません．しかし，順序集合に色々条件を付ければこの方法も 可能になります． 実際，計算機科学では，このような近似が可能な順序集合を使って，プログラムの 意味を段々近似していって定めるというような研究もあります．
前順序集合 (D, ≤) が
が成立することである．
これは具体例にあたってみると，ある程度この概念の意図が見えてきます．有向集合の典型的な 例は，すでに述べた部分関数の集合 PFun(A, B) の中に作ることができます．いま，A から B への関数（A 全体で定義されている部分関数) f0 : A → B を一つ取り，PFun(A, B) の中で，その定義されている ドメインでは f0 と一致する部分関数の集合を PFun(f0) と します．
PFun(f0) := {h∈PFun(A, B) | h(x)=f0(x) for x∈dom(h)}この集合が PFun(A, B) の順序で有向集合になることは次のようにして確かめられます．
h1, h2∈PFun(f0) とするとき，h3 をつまり，PFun(f0) に属する部分関数は皆，その定義域では f0 と 一致する訳で，任意の二つの部分関数に対して，それら「以上（≥）」の部分関数は，それらの定義域を合わせた定義域で f0 に一致している部分関数を選べばよい訳です．dom(h3) = dom(h1) ∪ dom(h2)とすれば，h1≤h3 かつ h2≤h3 になります．h3(x) = f0(x)
（全域）関数 f0の定義域の色々な部分を担う部分関数の上位の部分関数を
求めていった先には（全域）関数 f0 があります．したがって，PFun(f0)
は，色々な元が一つの元 f0 に
それで，これを何に使うかですが，これを収束させて，向かっていく元の極限を
作ることに使います．これは次の，
順序集合 (L, ≤) が，
dcpo の例としては，
D⊆PFun(A, B) を有向集合とします．このとき，次のような部分関数 f を とれば，これが D の上限 ∨ D になっています．dom(f) = ∪ h∈D dom(h)この定義で f(x) が一意に決まるだろうかという心配があるかもしれませんが， もし，x∈dom(h1) かつ x∈dom(h2) という二つの 部分関数 h1, h2 が D に合ったとしたら，D は有向集合ですから，h1≤h3 かつ h2≤h3 となる h3∈D があるはずなので，h1(x)=h3(x)=h2(x) となり， 同じ x に対しては１つの値が定まる事が分かります．f(x) = h(x) ただし h は x∈dom(h) となるような h∈D
また，これが D の上界の内で最小であることは，dom(f) を D の中の部分関数の どれかで定義されている元の集合に取ったことから分かるでしょう．
上では，その任意の有向部分集合の上限がある順序集合について学びました． ここでは有向集合からさらに限定した集合についてだけ上限が保証されている 順序集合を定義します．
順序集合 (L, ≤) が，ω-完備(ω-complete) であるとは， その任意の ω-鎖 (&omega-chain)x0≤x1≤x2≤ ...が L の中に上限を持つこととする．
ω-chain は，まず，鎖であり，従って有向集合ですから，任意の有向集合に対して上限を持つ dcpo は ω-完備ですが，逆はかならずしも成り立ちません．また，ω は， 集合 {0, 1, 2, ...} を表す記号です．こういう自然数に対応つけて作れる上昇列 （続く元が等しい場合も含む）に ついて上限がある集合がω-完備な順序集合です．
ここでは順序集合を完備束に埋め込む方法を見ていきます．例えば，有理数の集合 (Q, ≤) は，A = {x∈Q | x2≤2} は Q の中に上限を持ちませんが，Q を含む実数の集合 R は，そのなかに A の上限 √ 2 を持ちます．その結果，R の中では，Q の中だけでは展開できなかった，極限に関する 色々な理論の構築が可能になります注）．ここでは，このような，順序集合からそれを含む完備な 束をシステマティックに構成する方法を見ていきます．
注）正確には実数の集合Rは順序集合としては完備ではなく，Rに最小元と 最大元を加える必要があります．最大元を∞，最小元を-∞とすれば， R ∪ {-∞, ∞} が完備順序集合になります．
以下の項目へのリンク
(P, ≤) を順序集合とします．
完備束 (L, ≤) と P から L への順序を保つ写像 φ の組が，
一般に，完備束はそうでない順序集合よりも扱いやすいので，与えられた順序集合 (P, ≤) を完備な順序集合に拡張（完備化）したものを求めることができると 良いのですが，あまり大きすぎる完備束に拡張する必要もありません．例えば， 有理数の集合 Q を完備化し，R ∪ {-∞, ∞} を 求めることは有用であると思いますが，実は，この上に同じものを置いても， やはり，Q を埋め込むことができる完備束が得られます．こう考えると， 与えられた順序集合を完備にするのに最小限度の元を加えた完備化という概念が 考えられます．そのような概念として，（和）稠密（join dense）な完備化があります．
(L, ≤) を完備束とします．P⊆Lが
∀x∈L ( x=∨ {y∈P | y≤x} )が成立することであるとします．つまり，L の元はすべて P の元の有限あるいは 無限集合の上限になっているということです．もう少し砕けた表現で言い換えると，L は Q が完備になるのに必要最小限の元しか加えていない完備束ということになります．
上の図は L と P の間が随分空いているように見えますが，L のすべての元が P の元の集合の上限になるわけですから，P の元は L の中のいたるところに 存在しなければいけません．従って，イメージ的には次の図の方が正しいかもしれません．
上で述べた R ∪ {-∞, ∞} の中で有理数の集合 Q は稠密になっています．
いま，(L, ≤) を完備束，P⊆L として，L の中に P が稠密になる完備束 L'⊆L は存在するでしょうか？ 答えは yes です．L' として
L' := {∨ X | X は P の order ideal }とすれば，(L', ≤) は完備束で，P は L' の中で稠密になります．
稠密の概念を 順序集合 (P, &le) が，完備束 (L, ≤) に埋め込まれる場合にも 拡張しておきます．
完備束 (L, ≤) が埋め込み φ L → P で，順序集合 (P, ≤) の完備化 であるとき，これが P が（和）稠密（join dense） であるのは φ(P)⊆L が，(L, ≤) で（和）稠密であることとする．
ところで，順序集合 (P, ≤) が与えられたとき，その（和）稠密完備化は 同型を除いて一意に決まるでしょうか．この答えは no です．それは完備化に より，P の二つの下に閉じた部分集合 X1, X2⊆P に対して，
∨ X1 と ∨ X2 を一致させることも出来るし，また，別々の値を取らせる選択もできるからです．実際，下で紹介する（和）稠密な完備化では一つの順序集合に対して同型で ない完備束ができることがあります．
以下，ここでは順序集合 (P, ≤) が与えられたとき，これを完備束にする 次の３つの方法を述べます．
これらのうち，後ろの二つは，(P, ≤) が出来た完備束の中で（和）稠密に なる完備化です．これらを述べた後，後ろの２つの完備化については， 簡単な比較も行います．
(Q, ≤) を順序集合とします．このとき，Q の冪集合 P(Q) は集合の 包含関係 ⊆ で順序集合 (P(Q), ⊆) をなし，これはさらに完備束でも あります．Q は P(Q) へ
φ : Q → P(Q)で埋め込むことができます．φ(x) := ↓x = {q∈Q | q≤x}
これは一般には（和）稠密な完備化ではありません．実際，Q に極小元ではない u∈Q があれば，{u}∈P(Q) は
∨ {↓r | r≤u} = ∪ {↓r | r≤u}という形で表すことはできません．なぜなら，∪ {↓r | r≤u} は， u より小さな Q の元を含んでしまい， 一つしか要素の無い集合 {u} と等しくなることはないからです． したがって，この方法では，Q をかなり大きな完備束の中に埋め込んでしまいます．
これは，(Q, ≤) を order ideals の集合 O(Q) に埋め込む方法です．
φ : Q → O(Q)φ(x) := ↓x
(O(Q), ⊆) が完備束になることは完備束のところで説明しました． この中で，Q が（和）稠密になることは，∀X∈O(Q) に対して，
X は order ideal であるから，x∈X と ↓x⊆X は同値であり，となることから分かります．X = ∪ {↓x | x∈ X} = ∪ {↓x | ↓x⊆X} = ∨ {↓x | ↓x≤X}
これは，Dedekind-MacNeille の完備化とも言われます．
(P(Q), ⊆) から (P(Q), ⊆) への写像 M を次のように定義します．
M : (P(Q), ⊆) → (P(Q), ⊆)S∈P(Q) に対して，Su と Sd は， こちら で説明しましたが， 要するに，S の上界の集合と下界の集合です．M(X) := (Xu)d for X∈P(Q)
したがって，M(X) は，X の上界の集合の 下界の集合です．また，任意の X∈P(Q) に対して，M(X) は，order ideal です．従って，
MQ := M(P(Q)) ⊆ O(Q) ⊆ P(Q)
です．実は，(MQ, ⊆) は完備束になります．このMQを
Q の
φ(x) := ↓x for x∈Q
が埋め込みになります．
まず，(MQ, ⊆) が (Q, ≤) の（和）稠密な完備化になっていることを 証明しておきましょう．
これには MQ だけでなく，他の方法でも利用可能な汎用的な 証明手法を使います．M : P(Q) → P(Q) M(X) = (Xu)d は次の３つの性質を持っています．
このような性質をもつ関数を閉包演算子（closure operator）と 言います．これについては後の項目でも触れます．
MQ が完備束である証明に戻りましょう．いま，A⊆MQ とします．この時，A の上限 ∨ A は 次のように与えられます．
∨ A = M(∪A)
まず，MQ = {M(X) | X∈P(Q)} ですから，
次に，任意の X∈A に対して，
X ⊆ ∪A ⊆ M(∪A)であるから，
最後に，Y をA の任意の上界としたとき，∪A⊆Y
とならねばなりませんから，M(∪A)⊆M(Y)=Y となり，
従って，M(X)⊆M(∪{↓q | q∈X})
M(X)=X だから，X⊆M(∪{↓q | q∈X})
したがって， ∪{↓q | q∈X}⊆X
M は包含関係を保つから， M(∪{↓q | q∈X})⊆M(X)=X
順序集合 (Q, ≤) に対して，イデアルによる完備化 O(Q) とMacNeille の完備化 MQ={M(X)=(Xu)d | X∈P(Q)} は どちらも Q の冪集合 P(Q) の中に作った Q の（和）稠密な完備化ですが， 一般にイデアルによる完備化の方が大きくなります．
ここでは簡単な順序集合 (Q, ≤) に対して，これら二つの完備化を求めてみて， 結果を比べてみておきましょう．
元になる順序集合としては次のものをとります．
これは有限順序集合ですから，これを 含む有限の束を作りさえすれば，完備束ができる訳ですが，一応，二つの方法で 異なる束ができます．
まず，order ideal による完備化から見ていきます．(Q, ≤) の order ideal を すべて書き出すと，
{a, b, c, d}, {b, c, d}, {b, c}, {c}, {d}, {}です．次の図に，これらを集合の包含関係で完備束と見たものと，その完備束への Q の埋め込みを書いておきます．
次に，MacNeille の完備化がどうなるか見てみましょう．Q のすべての部分集合に 対して，M(X) = (Xu)d を取ると
{a, b, c, d}, {b, c}, {c}, {d}, {}となります．order ideal {b, c, d} が無いことに注意してください．次の図に この完備化とQ の埋め込みを書いておきます．
最後に，order ideal による完備化と MacNeille の完備化を並べて書いておきます．
MacNeille の完備化で MQ = {M(X) | X∈P(Q)} が完備束であることを示すのに，M が３つの性質を持つことを使いました．一般に，完備束 (L, ≤) から
自分自身への写像 c : L → L が次の３つの条件を満たす時，c を
MacMeille の完備化で使った M は，冪集合がなす完備束 ((P(Q), ⊆) でこれらの性質を満たしていました．
L が完備束で c : L → L が閉包演算子のとき，実は，
c(L) = {c(x) | x∈L} ⊆ Lは，また完備束になります．
これを証明しておきましょう．
A⊆c(L) とします．A に対して，その上限 ∨A が (c(L), ≤) に 存在することが 言えれば，c(L) は完備束になります．この上限は，(L, ≤) の中の A の上限とは 異なるかもしれません．実際に，(c(L), ≤) での A の上限は c(∨A) で 与えられます．ここで ∨A は，(L, ≤) での A の上限を表します． つまり，A の c(L) での上限は，A の L での上限に c を作用させることにより 得られると主張している訳です．まず，a∈A に対して，a≤∨A ですから，c(a)≤c(∨A) であり， a∈c(L) ですから，a=c(a) となり，c(∨A) は A の上界の一つであることが 分かります．
次に，y∈c(L) が A⊆c(L) の上界だったとします．これは ∨A≤y を意味しますから，c の２番目の性質により，c(∨A)≤c(y)=y となり，c(∨A) が c(L) の中で A の最小上界，つまり，上限であることが 分かります．
このように，完備束 L と閉包演算子 c に対して，c(L)⊆L は完備束に なることを示すことができました．
この項目の内容
ガロア接続は，二つの順序集合 (P, ≤) と (Q, ≤) がお互いに相手を拘束する 関係です．数学ではある領域の性質を解析するのに，他のよく分かっている領域の 知識を利用することがあります．そのときよく使われるのが準同型写像です．例えば，
f : P → Qという準同型写像があれば，P で順序に関して成り立つ性質は，f で運ばれた 先の Q でも成り立ちます．また，Q の性質も
全部の情報を持ち帰ろうとすれば，f は同型写像で ある必要があります．しかし，P と Q が同型で，片方はよく分かっていて，もう片方は まったく分かっていないという状況がそれほど沢山発生するとも思えません．ガロア接続は，準同型の一種ですが，一般の準同型写像よりは制限のきつい，そして，同型写像ほどは制限がきつくない，二つの 順序集合の間の関係を規定します．その結果，ある程度はお互いの順序集合の中の 情報を相手に移すことができます．
順序集合でのガロア接続という概念が認識されたのは比較的最近で，２０世紀に 入ってからのようですが，これはその名の通り，加減乗除と根号だけによる代数方程式の解法の存在を研究した １９世紀の数学者エヴァリスト・ガロアに由来しています．ガロアの理論の一番外側の 論理が，ガロア接続に基づいたものになっているのです．ガロア接続が， 順序集合の枠組みでとらえられてから，もともとのガロアによる代数方程式への利用を 超えて，色々な利用が研究されてきました． 記述のレベルが揃って無くて申し訳ありませんが，思いつくものを上げると，
のようなもので，ガロア接続が使われます．ここでは，ガロア接続の基礎的なことについて説明し， また，その応用についても軽く触れることにします．
ガロア接続には順方向のものと逆方向のものがあります．歴史的には逆方向のものから 始まったのですが，片方の順序集合の順序を逆向きにすることで，順方向に統一 できるので，この資料では順方向のものだけを扱います．その方が，ガロア接続同士を 合成するとき楽なのです．ちなみに，動機のところでも書きましたように， 歴史的には先だった 逆方向のガロア接続の代表的なものは，ガロアの理論で代数方程式が加減乗除と根号だけで 解けるかというあれの，一番外側の論理です．内側は，体(field)とか群（group）の代数的な扱いとかがあって， 私は苦手な領域ですが，一番外側のガロア接続に関しては，ほぼ順序集合とロジックの 話なのでそれほど難しくはなりません．
まずはガロア接続の定義を書いておきます．
(P, ≤) と (Q, ≤) を二つの順序集合とする．
このとき，順序を保つ写像 f : P → Q と g : Q → P の組が
x≤g(y) iff f(x)≤yfor ∀x∈P, ∀y∈Q
この定義は多分慣れない人にはとっつきにくいのではないかと思います． とっつきにくさは，二つあると思います．
一つ目についていうと，あることを定義するとき，「これこれの条件 C を満たすものをこれこれという」という定義で，条件 C が複雑になると 理解しにくくなります．数学を始めたばかりの人は，この C に論理記号が 入ると途端に理解しにくくなります．せいぜい，「かつ」，「または」だったら それほど難しく感じないのですが，ここに「ならば」が入ると，定義が二段階に なったような気がするのです（私はそうです）．あるいは，少しメタな定義に 感じます．しかし，「A ならば B」も「A でない または B」と言い換えられること ですし，それを頼りに場合分けに持ち込んでも良いし，あるいは，左の大小関係と 右の大小関係が必ず同時に起こると理解してもよく，なんとか馴染んでみてください．
二つ目の，関数適用前の素の値 x と y が一方の順序集合からでなく，双方から 提供されるのも，ガロア接続はお互いの順序集合が相手を拘束しあっているので， こうなるんだと思い，慣れることが必要だと思います．
結局，二つとも慣れろということでしかないのですが，まあ，慣れてください．
皆さんは，上の定義のところで書いた図で，順序関係がハッセ図とは違い，下が 大きいとして扱っていることに気がついたかもしれません．次の図に，上が大きいとした 定義を書いておきます．
この図では上の矢印が右から左と，普通と逆になってしまいます．それが
嫌で，私は定義の時に上下逆に書いたのです．でも，せっかく，上下を
ハッセ図と合わせた図を示したので，ついでに，それぞれの写像 f と g
がこの図の向きで，f は
定義だけであまり意味なく引っ張ってしまいました．ガロア接続の基本的な 性質に入る前に，ほんのちょっとだけ例にあたっておきましょう． 定義が分かりにくいので，この先，抽象的な定義だけ持って議論を進めるのが 辛いかもしれないからです．
ここではごく簡単な例をいくつかと，ガロア接続にならない設定の例について 見ていきます．
まず最初に，ちょっと当たり前に思える一連の例を示します．ただし，これらは，
ガロア接続の本質をある程度表していますので，あまり飛ばさないで見ていく方が
良いです．次にガロア接続にならないものについて例を示し，最後に少し自然な
例をいくつかご紹介します．例が沢山ありますが，ゆっくり見ていってください．
あと，上下の関係が揺れて申し訳ありませんが，次の一連の例では
まず，P と Q が同型写像 f で同型なら，g = f-1 として，それらはガロア接続をしています．これはいちいち証明するより，次の図のような簡単な同型の順序集合の 対応をみて納得してください．左右，同じ形をしているので対応する元の組の大小関係が 同値であるのは当たり前な訳です．
このとき，f : P → Q は，P のすべての元を α に飛ばします．逆に g : Q → P は，g(α)=max(P)=a とします．
これがガロア接続になっていることは次のようにして確かめられます．
任意の x∈P に対して，f(x)=α となります．y∈Q は α しかありませんから，g(y)=g(α) = max(P) と なります．
従って，
g(y)≥x iff y=α≥f(x)=α
となり，ガロア接続の条件が満たされます．
要は，左右の順序集合共に大小関係が成立する場合しかないので，同値な訳です．
これは上の逆のケースです．P の唯一の元を Q の最小元 min(Q) に飛ばすことが 上とは異なります．証明は各自でやってください．
上２つの組合せです．P の元はすべて，f で Q の最小元に飛ばし， Q の元はすべて，P の最大元に飛ばします． x≤g(y) も f(x)≤y も常に成り立つ不等式ですから，これらは同値になります．
これは最初に述べた例と直前の例の組合せです．同型となる芯の順序集合が P と Q にあり，P側では芯の元にそれより小さい元をくっつけます． 逆に Q 側では芯の元にそれより大きい元をくっつけます．f も g も 芯の元については，その対応通り飛ばします．また，芯の元にくっつけられている 元については，くっついている元が飛んでいくところへ飛ばします．
これがガロア接続になることはなんとなく分かるでしょう．(^_^)
次の図のような２つの順序集合 (P, ≤) から (Q, ≤) があり，P から Q に 順序を保つ写像 f が設定されているとします．この状況で，f とガロア接続をなすような 順序を保つ写像 g : Q → P はあるでしょうか？
ここの例題のタイトルからして分かると思いますが，そのような g : Q → P は 存在しません．キーは，Q の β をどこに飛ばすかです．β を飛ばす先を考えてみます． P の b と c は 対称的ですから，どちらか一つで良いとして，可能性としては a, b, d のどれかに 飛ばすことになります．このどれもガロア接続の条件を満たさないということを 言えば良い訳です．これは次の図のようにβをこれらのどれに飛ばそうが，ガロア接続の 条件を満たさない元の組が出来てしまいます．
したがって，この f に対応するガロア接続 g は存在しません．ただし，同じ 順序集合同士でも写像が違えば，存在することもあります．例えば，
では，g として，αとβを a ，γを d に飛ばせば，ガロア接続になります．
これは本当は，記号論理でやったほうが感じがでるのです．記号論理では A ∧ X と A→Y がガロア接続をなします．でも，記号論理で説明する ためには，その枠組みを説明しなければなりませんので，ここでは殆どの人が 知っている集合論に置き換えた例を示します．¬A は A の補集合を表すと 思ってください．記号論理の A→Y は¬A ∨ Y ですから，集合の ¬A ∪ Y に対応している訳です．
これがガロア接続であることを示すためには，X⊆(¬A∪Y) から A∩X⊆Y が導かれ，またその逆も導かれることを言えば良い訳です．
X ⊆ (¬A∪Y) ならば A∩X ⊆ A∩(¬A∪Y) = A∩(¬A) ∪ A∩Y ⊆ Yここでは集合でやりましたが，形式論理で「かつ（and）」と「ならば（implies）」は ガロア接続をなすのです．したがって，A∩X⊆Y が言えました．
逆に， A∩X ⊆ Y ならば ¬A ∪ (A∩X) ⊆ ¬A∪Y
左辺を展開すると
¬A ∪ (A∩X) = (¬A∪A)∩X = X なので
X ⊆ (¬A∪Y) が言えました．
位相空間と言うと難しそうに聞こえるので，具体的に平面 R2 で，普通の開集合と閉集合が定義されている状況を考えます（ここでは 閉集合だけを扱います．閉集合は全体の空間からある開集合を取り除いた 形で表される集合のことですから，まあ，どちらも定義されている訳です）．
ここでガロア接続の左側の順序集合としては， P(R2) を集合の包含関係で順序を付けた順序集合 (P(R2), ⊆) を考えます．また，右側の順序集合 としては，R2 の閉集合すべての集合C(R2) をやはり，集合の包含関係 ⊆ で順序付けた順序集合 (C(R2), ⊆) を考えます．
このとき，
f : P(R2) → C(R2) f(X) は X に集積点を加える写像．はガロア接続をなします．きちんと証明しようとすると位相空間の知識が要りますから，次の図をみながら，左右の順序関係の同値は成り立ちますよねと納得してください．これは X を含む 最小の閉集合を割り当てる写像とも言いかえられる． 感覚的に言うと，図形 X の縁がついていない部分に縁をつける写像．g : C(R2) → P(R2) g(Y) = Y つまり恒等写像
二つの順序集合 (P, ≤), (Q, ≤) が，f : P → Q と g : Q → P で ガロア接続をなしているとします．このとき，次のことが成立します（証明は後でします）．
f(g(y))≤y for ∀y∈Q
したがって，
したがって，
思い出しように定義の図を再掲しておきます
ここで，関数
cl(x) := g(f(x)) cl: (P, ≤) → (P, ≤)
ker(y) := f(g(y)) ker : (Q, ≤) → (Q, ≤)
と定義すると，上の性質と，f も g も順序を保つことから，cl は性質
を満たします．これらは，以前述べた 閉包演算子 の性質です．要は，ガロア接続からは閉包演算子ができる訳です． したがって，cl(P)⊆P は完備束です．
同様に ker=f(g(y)) は次の性質を満たします．
cl とは，一番目の不等号の方向が逆になっただけです．こういう演算子を
では，f と g に関して最初に述べた二つの性質 を証明しておきましょう．証明すべき式は次の通りです．
f(g(y))≤y for ∀y∈Q
これらのうちの，g(f(x))≥x と f(g(f(x))) = f(x) だけ証明します． 残りは同様に証明できます．
まず，g(f(x))≥x から証明しましょう．
x∈P を任意にとります．x を f で飛ばした Q の中で，f(x)≤f(x)
です．したがって，次の図のように，下の方の f(x) を g で P に戻すと，ガロア接続の条件から
g(f(x))≥x
を得ます．
Q.E.D.
つぎに，f(g(f(x))) = f(x) を証明します．
f(g(f(x)))≥f(x)
を得ます．あとは，この逆の不等式を証明すれば左右が等しいことが分かります．
それには次の図のように，P の中で
g(f(x))≤g(f(x))
であることを使い，
図の右側のように
f(g(f(x)))≤f(x)
を得ます．
これで
f(g(f(x))) = f(x)
が証明されました．
ここまでを纏めると，上記でガロア接続の基本的な性質が証明され，また，
ker(y) := f(g(y))
ところで，
話を単純にするために閉包演算子だけを考えます．答えとしては，
(P, ≤) を順序集合とする．cl : P → P が閉包演算子である場合，
次の２つの順序を保つ写像の組は (P, ≤) と (cl(P), ≤) の間の
ガロア接続をなす．
f(x) := cl(x)
g : cl(P) → P
g(y) := id(y) := y
このように g が埋め込み（中への同型写像）である場合のガロア接続を
次にもう一つ，ガロア接続の非常に重要な性質を言います．それは
(P, ≤) と (Q, ≤) をそれぞれ一つ書くとゴチャとして
これは f・g・f(x) = f(x) であることと，g・f・g(y) = g(y) であること，および
f, g は順序を保存する関数であるので，同型写像であることが分かります．
上でみた例の中に，同型の順序集合に各元に片方は下に元をつけ，片方は上に元を
つけてガロア接続を作ったものがありました．あれは，この定理に基づいている訳です．
つまり，大雑把に言えば，
ガロア接続のこの性質は，
先に少し人為的な例をご紹介しましたが，ここでは多少は応用があるのではないかと
感じられる
形式的概念分析は次のガロア接続に基づいています．
A と B を二つの集合，R ⊆ A × B を A と B の間の二項関係とする．
このとき冪集合 (P(A), ⊆) と (P(B), ⊆op) は，次の写像でガロア接続をなす．ここで，⊆op は，⊆ の逆の順序と
する（つまり ⊇ だが，単独で出てきたとき，どちらの向きかをすぐ見て取れないので明確に分かる印 op (opposit の略) を付けて記す）．
f(X) := {y∈B | (x, y)∈R for ∀x∈X}
for X∈P(A)
g : P(B) → P(A)
g(Y) := {x∈A | (x, y)∈R for ∀y∈Y}
for Y∈P(B)
f, g の式は直感的に解釈しにくいと思いますので，上の定義を図にしておきます．
写像 f は，A の部分集合 X に対して，X の要素すべてと R の関係になる B の要素
すべてからなる集合 f(X)⊆B を割り当てます．X が大きくなると，それだけ
沢山の A の要素と R の関係になることが必要になりますから，f(X) は小さくなります．
逆の写像 g は B の部分集合 Y に対して，Y の要素すべてと R の関係になる A の
要素すべてからなる集合 g(Y)⊆A を割り当てます．こちらも，Y が大きくなると，
それだけ沢山の B の要素と R の関係になることが必要になりますから，g(Y)
は小さくなります．
このように f も g も引数の集合が大きくなるほど，結果は小さくなるという性質を
持っています．このガロア接続は，自然に表現すると逆向きのガロア接続になります．
このページでは順方向のガロア接続しか説明していませんから，ここでは，
P(B) 側の順序を ⊆ の逆 ⊆op にして順方向の
ガロア接続として定義しています．
これがガロア接続になっていることを確認するためには
つまり
ここでは，これがガロア接続になっていることについてさらに見ていくのではなく，
このガロア接続が持つ意味というか，応用の可能性について説明したいと
思います．
上の説明では集合 A と集合 B を全く対称的に扱ってきました．しかし，ここで
と思ってみます．例えば，A を太陽系の惑星の集合，B は
惑星が持っている，「太陽から近い」，「比重が重い」，「直径が小さい」，
「軌道が円に近い」などの属性です．ここで属性は真偽の値を取るものを扱います．
他の例としては，A を「猫」，「犬」，「トカゲ」などの動物の集合として，
B を「子供を生む」，「卵を産む」，「体温が一定」などの属性を考えてみて下さい．
このような設定では，例えば，惑星の例では，関数 f : P(A) → P(B)
に関しては，f(X) は，X の中に指定された惑星すべてが持つ共通の属性すべてを表します．また，逆の写像
g : P(B) → P(A) において，g(Y) は Y の中に指定された属性すべてをもつ惑星の集合を
表します．そして，このガロア接続は，
では，以下，この
それには X1⊆A から f(X1) を求める過程，逆に Y1⊆B から g(Y1) を求める過程を
細かく追いかけていくことが参考になります．
まず，モノの集合 A の部分集合 X1 をとります．次の図の左下の箱です．
この X1 から f(X1) つまり，X1 の要素が共通に持っている B の属性の集合を求めます．
図の右側の箱です．さらに，この属性の集合 f(X1) を満たすすべての A の元の集合
g(f(X1)) を求めます．実は，これが X1 に戻らず，最初に無かった A の元を含むことが
あります．例えば，動物とその属性の例では，{ネコ，ネズミ，イヌ} の共通に持つ
属性を求めて，今度は逆にその属性をすべて満たす A の中の動物を求めたら，キリンや
像が入って来たといった場合です．今度は，さらに g(f(X1)) から，それらが共通に
満たす属性の集合 f(g(f(X1))) を求めますと，これは f(X1) に一致してしまいます．
g(f(X1)) は，属性 f(X1) をすべて満たす最大の集合だからです．
まあ練習ですから，今度は逆に属性のある集合 Y1⊆B からはじめて，g(Y1) を
求める過程を追っていきましょう．次の図の右下の箱 Y1 はある属性の集合とします．
この属性すべてを持っている A の要素を求め，それを 左の箱の g(Y1) とします．
ここでさらに，g(Y1) に属するモノが共通に持つ属性の集合 f(g(Y1)) を求めると，これは Y1 より
大きくなる可能性があります．なぜなら，Y1 の属性を共通に持つモノの集合が g(Y1)
であって，それらが Y1 以外の属性を共通に持っていてはいけないと言うことはないからです．もちろん，Y1 に一致しても良いのですが，可能性としては Y1 より大きくなる可能性もあります．
次に，f(g(Y1)) から，その属性をすべて満たすモノの集合 g(f(g(Y1))) を求めると，
g(Y1) が，これらの属性を共通でもっているモノの集合ですから，g(Y1) となります．
このようにして，f と g でお互いに移りあう A と B の部分集合に，
それぞれ，f と g でそれらの集合に移る集合がくっついているような
状況ができます．これらの集合は f(X1), g(f(X1)) に含まれる（⊆）という
関係になっています．
今までは，分かりやすさを優先して ⊆op を使わないで説明して
きましたが，順方向のガロア接続として扱うためには P(P)(B) は順序関係を
逆にする必要があります．ここで，上と同じ内容の図を，B 側の方向を逆にして示して
おきます．そうしないとさらに議論を展開するとき，面食らうからです．
まあ，このように A 側と B 側で，くっつく方向が逆になっている訳ですね．
このような対応がある状況で，例えば，集合 X1' の要素を減らして行って，
集合 X2'⊆X1' を作ってみます．ある程度まで減らしても f(X2') の
値は変らないかもしれませんが，沢山減らすと，
それらが共通に持っている B の属性は
増えて，次の図のように集合 f(X1) を真に含んでしまう可能性があります．
これを f(X2') とすると，これに対して，再度，g(f(X2')) という，A 側の
X2' がぶら下がっている集合ができ，この g(f(X2')) と f(X2') が相互に
対応します．
このようなことをずっと続けると，A の冪集合の中と B の冪集合の中に
f と g でお互いに対応しあう同型の部分集合の系ができる訳です．
このとき，A 側と B 側は，集合の包含関係は逆向きになっていることに
注意してください．
こうやって出来た同型の「芯」をモノの集合 A と属性の集合 B ，そして，
A と B の関係から導き出される概念システムととらえるのが，
モノの個数や属性の個数が増えると，この同型の「芯」はすぐ大きくなります．
世の中には，この「芯」をビジュアルに見せるツールやなにか解析を支援する
ツールが開発されているそうです．私は使ったことがありませんが，参考文献
のところにあげた解説論文
に紹介されていますので興味のある人は調べてみて下さい．
この形式的概念分析の終わりに非常に簡単な例を使って，どのような概念の束が
できるのか具体的に見てみましょう．ここでは，次のような二項関係から
概念の束を作り出してみます．
この例での，モノの集合 A は，動物の種類の集合
上の表で，１つの動物，例えば，トカゲだけからなる集合 {トカゲ}に対して，その共通の属性 f({トカゲ}) は，表における
トカゲ の表を横に見ていって，●のついている属性を拾っていけばよいので，次のように
なります．
ここでいちいち計算する訳にいきませんので，別途計算した動物のグループの
束を次の図に表示しておきます．順序は「上が下を含む」という関係です．
どうでしょう．図を見て，「なるほど納得のいく動物のグループが出てきたな」と
思うでしょうか．
あるいは，「気が付かなかったけど，そういえば，こういう属性の共通性に着目すれば
このような動物のグループができるのか」というような気付きはあるでしょうか．
本来は，さらに，これと同型対応する属性の集合の束があり，それを左右に表示すると
カッコ良いのでしょうが，図が大きくなってそのような図を描くのは難しいので，
先ほどの図の動物のグループの下に対応する属性の集合を書いてみました．
この図のそれぞれの四角形の中には上は動物のグループ，下はそのグループで共通の
属性の集合が書かれています．属性のグループは上ほど，属性が少なく，
動物のグループは下ほど動物が少なくなっていることに注意してください．
つまり，二つの同型の束では，包含関係の向きが逆になる訳ですね．
まあ，これは，小さな，しかも，私が作った拙い例ですから，なかなか，
現実に近いデータでどうなるか，ピンと来ないかもしれません．
実は，私も形式的概念分析の具体例を自分で処理してみたのは，今回がはじめてでした．
そこで感じたのは，当たり前ですが，次のようなことを感じます．
この項目は沢山書いたので，まとめを作っておきましょう．
関数の合成
これらの性質をもつ関数 g・f を
関数の合成の順番を逆にした
逆に，上の３つを満たす閉包演算子
以上，ざっとこの項目で学習したガロア接続のことについてまとめました．この中で
最後に書いた同型のことについては重要ですから，補足と，イメージを掴みやすいように
図を補足して，この項目を終わることにします．
(P, ≤) と (Q, ≤) の間にガロア接続 f : P → Q と g : Q → P
があるときは，それぞれの順序集合の中に芯となる同型な順序集合
P と Q の中には f と g でお互いに移りあう同型の芯となる順序集合 g(Q)⊆P
と f(P)⊆Q があります．図では，それらの順序集合の要素は赤い大きな円と
青い大きな円で表示されています．それ以外の要素は，相手側の順序集合の中の
大きな円で表されている要素に f と g で飛ばされます．例えば，左下の点線で囲った中の x1∈P
がそうだとしてみましょう．x1 が f で飛ばされる先が，右側の f(x1) だとします．
f(x1) は同型の芯の要素ですから，f, g でお互いに移りあう f(g(x1))∈P が
あります．x1 はこの要素 g(f(x1)) の下についています（x1≤g(f(x1))）．他にも
g(f(x1)) には，g・f で，この要素に飛ばされる要素が下についているかもしれません．
順序集合 Q 側では，f・g で f(x1) に飛ばされる要素が，P 側とは逆に f(x1) の上に
いくつかついている可能性があります．
このように，ガロア接続とは，
P と Q に同型の芯になる要素同士が f と g で対応し，P では芯の要素の下に，
Q では芯の要素の上に複数の（0個以上の）要素が付随し，それらは f と g で相手側の芯の
要素に飛ばされるという構造であると言うことができます．
以上で，ガロア接続の
項を終わります．
ガロア接続に関する基礎や応用を勉強するのに有用な文献をあげておきます．
まず，いま証明した g(f(x))≥x の両辺に f を作用させると，f が
順序を保つことから，
cl(x) := g(f(x))
とおくと，cl は閉包演算子，ker は， kernel 演算子になるということが分かった
訳です．
f : P → cl(P)
(P, ≤) と (Q, ≤) を順序集合として，順序を保つ写像 f: P → Q と
g : Q → P がガロア接続をなすとする．このとき f(P)⊆Q と g(Q)⊆P は順序集合として同型になる．
そのときの同型写像は g : f(P) → g(Q) と f : g(Q) → f(P) である．
分かりにくいので２つずつ書いている．
f : P(A) → P(B)
を証明すれば良いことになります．これについては，時間があるとき
皆さん自身でやってみてください．
太陽系の惑星のあるグループ ↔ 惑星に関する属性の部分集合
の対応を決めることになります．
2021.03.08 (月)
2021.03.09 (火)
{トカゲ，ネズミ，イヌ，スズメ, フナ, ウサギ}
です．これらの属性の集合は
{卵を産む, 哺乳する, エラ呼吸をする, 肉を食う, 植物を食う, 前歯が発達している,
飛ぶ}
とします．私が思いつくものを適当にあげましたので，何か偏っているかもしれませんし，
上の表で●を付けているところも間違いがあるかもしれません．．
とりあえず，これでどんな感じの束ができるのか感触を見てから，必要に応じてもっと詳しい
参考文献にあたってみて下さい．
f({トカゲ}) = {卵を生む, 肉を食う}
概念の束は，動物の集合の色々な部分集合 X に対して f(X) を計算していく訳ですが，
f({ネズミ}) = {哺乳する, 肉を食う, 植物を食う, 前歯が発達している}
f({イヌ}) = {哺乳する, 肉を食う, 植物を食う}
f({スズメ}) = {卵を生む, 肉を食う, 植物を食う, 飛ぶ}
f({フナ}) = {卵を生む, エラ呼吸をする, 肉を食う}
f({ウサギ}) = {哺乳する, "植物を食う, 前歯が発達している}
f(X1 ∪ X2) = f(X1) ∩ f(X2)
ですから，X⊆A に対する f(X) の集合は，上の f({トカゲ}), f({ネズミ}), ... の
集合から，次々に共通集合を作り出していって，新たな共通集合が出来なくなるまで
続けたものになります．そして，そうやって作った属性の集合 Y から逆に，Y の中の
属性をすべて満たす動物を集めた集合 g(Y) を作り出していったものが，それらの属性の
集合に対応する動物のグループになる訳です．
たぶん，世の中のツールでは，このような点にもなんらかの工夫が
あるんだと思いますので，参考文献
や，そこでさらに参照してあるものなどを調べてみると面白いのだと思います．
通常，我々が認識する属性は多値のことがあり，それを数個の二値の属性に
翻訳するのは面倒だということ
属性間に依存関係があるものがあり，属性の集合 B の部分集合の中には
存在しない部分集合があり得る．そういうものは除外して考える必要が
ありそうなこと
やはり，モノの集合や，属性の集合が大きくなると，急速に概念の束は
大きくなるので，人間にとって見て取りにくくなり，分析をおこなったり，
知見を得るのに，なんらかのサポートが
欲しいこと
2021.03.10 (水)
(実は，
はガロア接続になっています．
( P⊇)
があり，その他の要素は，それらの芯に g・f や g・f で飛ばされるという構造をしています．
次の図はこの状況を感覚的に良く表していると思います．
2021.03.12 (水)
後，ここの参考文献とも被りますが，
ガロア接続の基礎と特に数理論理学への応用の良い解説論文です．
この論文の内容については，私のページ
The Galois Connection between Syntax and Semantics by Peter Smith
(構文と意味の間のガロア接続)についての紹介
でもう少し詳しく説明しています．
ガロア接続の一つの応用分野である形式概念分析（formal concept analysis）に関する
解説論文．非常に分かりやすいです．形式的概念分析のツールの紹介もあります．たぶん，PDF
をダウンロードできると思います．
2021.03.07 時点で見てみましたが，
これは計算機屋さん向けのチュートリアルです．不動点の話と絡めて解説してあります．
かなり計算機よりの話で具体例が沢山書いてあります．
文献リスト：計算機科学における Posets の利用・扱い(1)
にも，昔書いた参考文献のリストがあります．
計算機科学を先行している方は， {0, 1} の二値のブール代数には馴染みが深いと
思いますが，ブール代数としては，多くの値を持つ，より一般の代数の一群があります．
簡単に言うと，ブール代数とは，最小元と最大元がある分配束で，各元に補元と呼ばれる
論理学の否定相当の元が存在するような束を指します．
このページが大きくなり過ぎたなどの理由から，ブール代数については 別ページ
ブール代数（Boolean algebras）にまとめました．ご興味のある方は，そちらを参照してください．
フィルターのうち，極大なものを超フィルター（Ultrafilter）と言います． これは，例えば，実数の集合を無限小のようなものを入れて拡張する超準解析 などで使われたり，ちょっと意外な使われ方をします．この項目では超フィルターの そういった側面を説明していきたいと思います．
このページが大きくなり過ぎたなどの理由から，超フィルターについては 別ページ
超フィルター（Ultrafilter）にまとめました．ご興味のある方は，そちらを参照してください．
ハイティング代数は，束の一種ですが，直観主義論理のモデルに使われるなどの 用途があります．上で述べたブール代数もハイティング代数の一種ですが，ハイティング 代数の中には，ブール代数よりも「弱い」代数があり，これらは，排中律 p ∨ ¬p が必ずしも成立しない論理のモデルとして使うことができます． ここでは，このような論理学との繋がりまでは解説できないと思いますが，ハイティング代数についての基本的な事柄を説明します．
このページが大きくなり過ぎたなどの理由から，ハイティング代数については 別ページ
ハイティング代数（Heyting algebras）にまとめました．ご興味のある方は，そちらを参照してください．
ここと次の項目は，Modular 束への親しみ方について書いています． 特に，Modular 束がどんな意味があるかや何に使えるかではなく，一見奇異に見える 定義に少しでも慣れれば良いというくらいの位置づけです．今のところ，他の項目とは あまり関係がないかと思います．Modular 束を束論の教科書などで勉強するとき， とっつきにくいなと感じた方がいらっしゃったら，読んでみるとよいかもしれません．
Modular 束は，
a ≥ c ならば a ∧ (b ∨ c) = (a ∧ b) ∨ c for ∀ a, b, c ∈ Lが成立する束です．Modular 束は， 束論の初学者には分かりにくい概念ではないでしょうか． だいたい，何に使えるか分からないし，形も不等式の条件が付いていて変だし．
または
a ≤ c ならば a ∨ (b ∧ c) = (a ∨ b) ∧ c for ∀ a, b, c ∈ L
これが何に使えるかは，私も良く知りません．なんでも Dedekind が束論の前身を考えているとき アーベル群の部分群がなす束の性質として認識していたというような由緒正しい 性質だそうですが．
上の２つの等式は双対(dual) で，一方から一方が言えますので，上の方だけにして， さらに，任意の束で成立する
a ≥ c ならば a ∧ (b ∨ c) ≥ (a ∧ b) ∨ c for ∀ a, b, c ∈ Lを考えます．この不等式はどんな束でも成立するもので，Modular 束は，この不等式に おいて常に等号が成立することを保証するものです．
Modular 不等式は Distributive 不等式の特別な形ですから，まず，
a ∧ (b ∨ c) とそれを展開した式 (a ∧ b) ∨ (a ∧ c)を頭に思い浮かべます．そしてじっと見つめて，この二つのどちらが大きいかを 考えます．
左辺の a は右辺の (a ∧ b) と (a ∧ c) 以上であり，また， 左辺の (b ∨ c) も 右辺の (a ∧ b) と (a ∧ c) 以上な訳ですから， ∧ をとっても それら以上となり，不等号は ≥ となります．これで次の Distributive 不等式が得られます．
a ∧ (b ∨ c)あとは，この式の右端の (a ∧ c) を c にすることを考えます．a ∧ c = c は a ≥ c と同値ですから，その条件を前につけて，Modular 不等式≥ (a ∧ b) ∨ (a ∧ c)
a ≥ c ならば a ∧ (b ∨ c) ≥ (a ∧ b) ∨ c for ∀ a, b, c ∈ Lを得ます．こうやってよく見ると，文字や演算子は変わらないのに，括弧の位置が変わるだけで大きさが変わる面白い不等式です．
このようにして，まず Modular 不等式に慣れ親しんで，いつでもこの式を展開 できるようにしておくと，束論の本で Modular 束の章を読むのは多少楽になるのでは ないかと思います．何に使えるかはまた別のところで学ぶことにして．
ところで，上の図は慣れたら次の図でも良いかもしれませんね．
あと，ここで述べたことを，
半順序集合に関する可視化の実験に載せておきます．
束 L が， Modular であるための必要十分条件は，次のようなペンタゴン（５角形） が L の部分束として存在しないことというのはどの教科書に説明されていると思います．
束 L が， Modular であるための必要十分条件は，次のようなペンタゴン（５角形） が L の部分束として存在しないことである．
(ここでの条件は，ペンタゴンが部分束として存在しないことであることに
注意しておいてください．束の中の大小関係を結んでペンタゴンがあっても，
束の演算 ∨ と ∧ に関してペンタゴンが形成されなければ OK です．)
また，Modular 束 L では任意の a, b ∈ L に対して，区間 [a, a ∨ b] と 区間 [a ∧ b, b] は，写像 x → x ∧ b と y → y ∨ a で同型になります．これはダイヤモンド定理と呼ばれます．
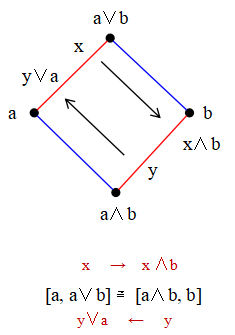
束 L が Modular とするとき，
区間[a, a ∨ b] と 区間 [a ∧ b, b] は，
写像 x → x ∧ b と y → y ∨ a で
同型となる．
図で
ペンタゴンが無いというのは Modular 束になる必要十分条件ですが，ダイヤモンド定理の 区間[a, a ∨ b] と 区間 [a ∧ b, b] が同型というのも Modular 束になるための 必要十分条件です．それを確信するには，
ペンタゴンがない <=> 区間[a, a ∨ b] と 区間 [a ∧ b, b] が同型を言えば良い訳です．=> はダイヤモンド定理の内容自身ですから，<= を言えば完了です．それには対偶をとって，ペンタゴンがあれば，区間[a, a ∨ b] と 区間 [a ∧ b, b] が同型に ならないことを言えば良い訳です．a = β, b = γ ととれば，同型にならない場合が作れますから，結局，この２つの条件は同値だということがわかります．上の同型が成り立つのが Modular 束だと言われると，Modular 束が何に使えるのか分からなくとも，
そういえば，最近，ペンタゴンの図として五角形らしい五角形でなく，下の図のような，ひし形に近い五角形を 使うのをよく見ているような気がします．δに対応する要素が区間 [β, α] の中に無いという図ですね．
このペンタゴンについても立体視の図がありますからリンクを貼っておきます．
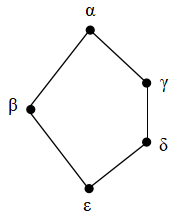
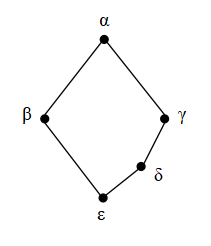
一応，Dilworth の定理も書いておきます．
順序集合 P において，w(P)が有限なら，w(P) = c(P)ここで，w(P) は P の中の最大の anti-chain の要素の数，c(P) はP を chain で 覆うときの最小の chain 数とする．
順序集合 P に対して w(P) と c(P) を図示しておきます．
以下は，J.B. Nation の第１章での Dilworth の定理の証明を理解するための 補助に書いた図です．
（次の図で Case2 がどんな時かは，図の後の注意を参照）
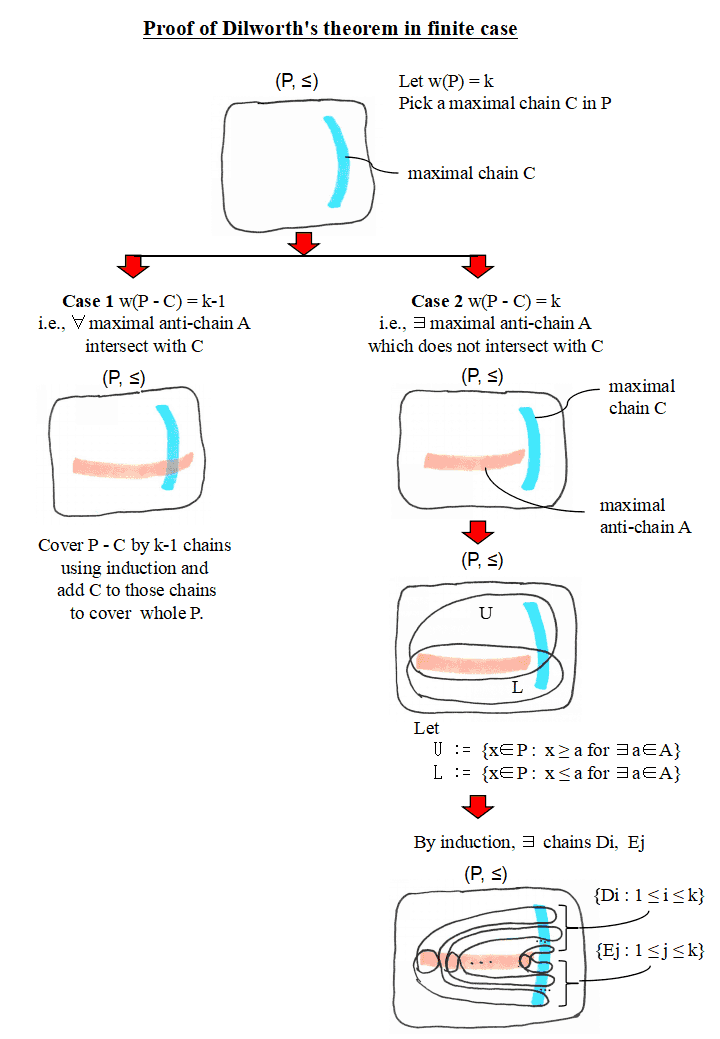
注意）maximal chain を取り去っても width が減らない例
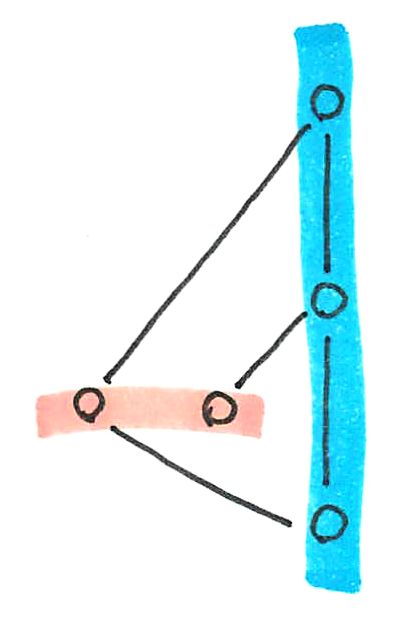
width 個の chains で覆うには，改めて，chain を取り直さないといけない．
この取り方は，定理の証明方法と同じ．
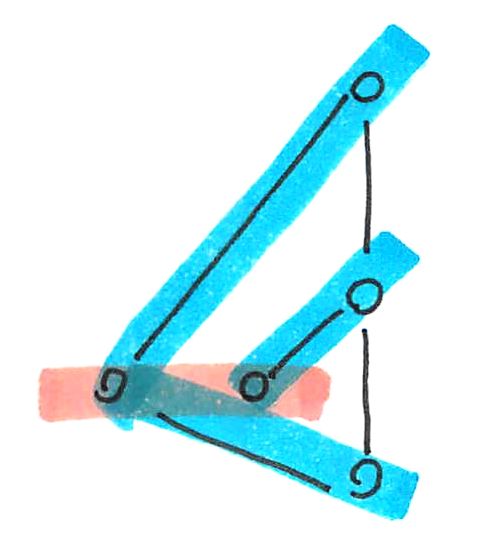
Join irreducible という概念は，有限個の join に表すことができない要素と いうことで，定義に否定を含んでいて，また，ほかに無限個の join で表すことが できないという completely join irreducible という概念も出てくるので， 結構，混乱しやすい．しかし，これは束を表現するためにとても重要な概念である． ここでは，定義を絵にしたりしながら，しっかりとこの概念を身につけていきたいと 思う．
まず，x ∈ P が join irreducible であるというのは，これが x とは異なる 要素 a, b ∈ L の join として表されないことである．つまり，
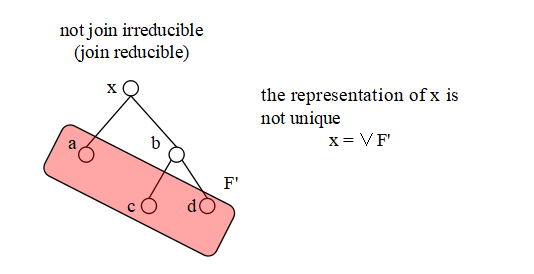
x = a ∨ b => x = a or x = bが成立すること．ただし，最小元 0 は，join irreducible な元には含めません（ 含める流儀もあるようですがここでは 0 は含めません）．join irreducible の定義は， 「表されない」と表現が否定形になっているので分かりにくいですね． 表されるとき join reducible と考えて，そうでないときと思ったら良いかもしれません． ここでは二つの元の join としましたが，これは「有限個」と言い換えても同じです． join irreducible でないときは，x は，複数の要素の join で表されている訳ですが， この表し方は下の２つの図に示すように一意ではありません．
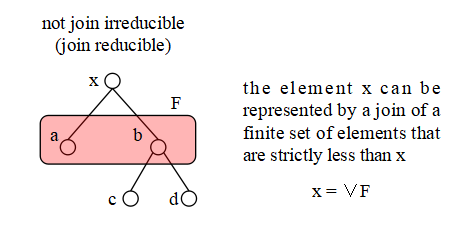
つまり，この例では x は次の図のようにも表すことができます．
だいたいにおいて join irreducible な要素は次の図のように直下の要素を一つだけ持つ要素です．
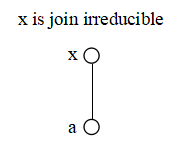
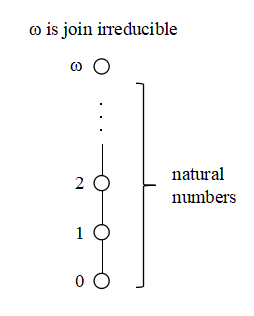
次の例の ω も join irreducible です．もともと w は自分自身と異なる有限個の要素の join で表せません．しかし，無限個の要素の join にはなっているので，completely join irreducible ではありません (無限個の join になっているとき，必ず自分自身がその中に含まれていなければならないとき completely join irreducible といいます)．
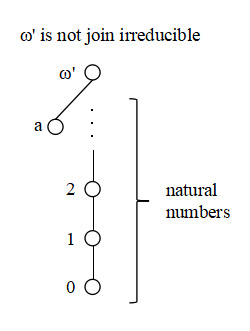
次の ω' は join irreducible ではありません．無限個の要素を使わなくとも a ともう一つ何か 自然数 n を選べば ω' = a ∨ n になるからです．
まあ，ここらあたりの絵を参考にしながら，しっかり join irreducible の概念を身につけてください．これは束の表現をするときにとても重要な概念になります．
/* ***** TO DO *****
米田のレンマとの関係
J.B. Nation の Notes on the Lattice Theory に Closure operator と 同等の概念として導入されている．私は他のテキストでは見たことがないような気が する (J.B. Nation 氏は，「今では普通の手法になった」と言われているが)．
便利なのだが私は分かりにくかったので解説を書いた．私と同様に分かりにくい人は
J.B. Nation の Notes on Lattice Theory への要望を参照していただきたい．
第二の要望 (Closure rules について)
第３章で書いてあることをまとめると次の図のようになります．
ここでは，ある特殊な種類の束の構造を学びます．それは代数の部分代数の族がなす束です． 特殊と言っても，結構よく現れます．なんせ，代数の部分代数の族ですから，代数が現れるところには現れる訳です．これが図の一番上の四角の中に書いてあることです．
次の四角の中は，代数的束 (Algebraic lattice) という束を定義するところを書いています． 代数的な束とはコンパクトな要素の集合がその束 L の中で join dense になっているという条件で 定義されます．この部分の四角の右側では，代数的閉包演算 (algebraic closure operator) という閉包演算および，その閉包演算により閉集合の族を定義し，それが先に定義した代数的束と 同等の概念だということを証明します．
次の四角は，代数的束の性質を記述するための概念をいくつか定義しています．
最後の四角は，そのようにして定義された諸概念で代数的束の性質を述べています．
一応，束の要素がコンパクトであることのイメージと位相空間の意味のコンパクトの対比も書いておきます．その要素がコンパクトとは，それが無限個の要素のジョインに押さえられていたら，その中から有限個の要素を選んで，そのジョインで元の要素を押さえることができるということです．位相空間では，コンパクトという概念は，ある集合が無限個の開集合のユニオンで覆われていたら，その中から有限個の開集合を選んでそれらのユニオンで覆うことができるということですから，うまく対応していますね．
