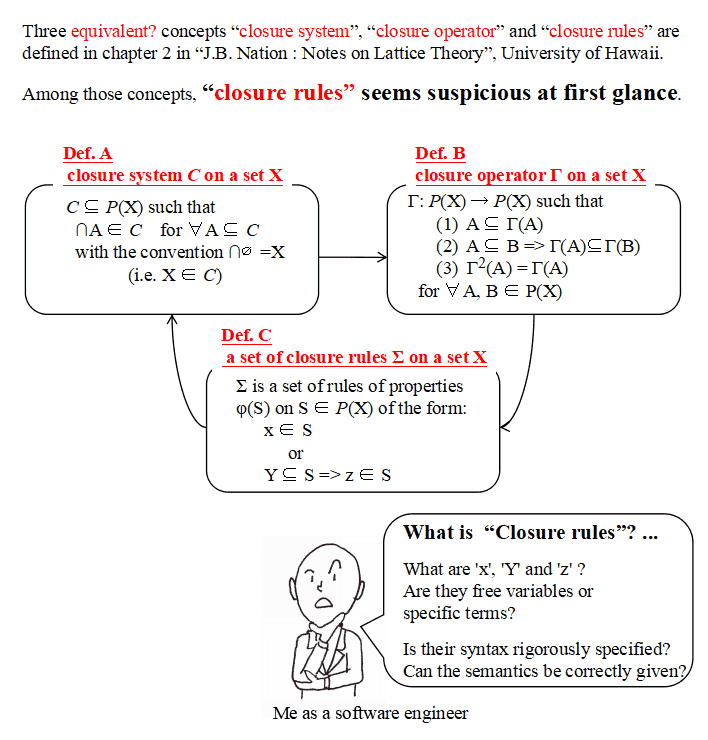
about "a set of Closure Rules"

First, I thank Dr. J.B.Nation that he made his precious text book on Lattice Theory public at his web-site:
J.B. Nation, Notes on Lattice Theory
(Seeing his web-site, he looks like the right scribble I drew.)
(Today, I asked Dr. J.B. Nation whether the contents of this page are correct or not and had a answer of 'yes'. I thank Dr. J.B. Nation for taking time to my question. 26th Oct. 2017)
x ∈ S ... (1)
or
Y ⊆ S => z ∈ S ... (2)
I misunderstood this definition. The point is shown in the following figure.
(In the above figure, P(X) means the set of all subsets of X, i.e., the powerset of X.)
I thought "a set of closure rules" as a set of somethings like formulae (formulae in such as first order logic) of a special form. So, questions arose such as
Examples are given in the text book.
However, these examples did not correct my misunderstanding that Σ is a set of formulae, because these examples are written in the form of natural language-like statement, and enhanced the feeling that they are written in a mathematical logic.
In the latter part of the text book, some concepts such as "algebraic lattice" depend on the concept of "a set of closure rules". So, I cannot leave the misunderstanding for the further reading.
After deep thinking, I found the wrong point. I realized that the definition of "a set of closure rules" does not refer to a 'concrete' set of formulae. I rewrite it as follows in the form with less misunderstanding.

The set Σ is only conceptually determined. It is not one that human can describe by e.g., first-order logic. Each pair (Y, z) ∈ Σ represents if Y is included in S, z is also a member of S. Y is sometimes a very big set of an infinite cardinality. Therefore (Y, z) i.e., a property "Y ⊆ S => z ∈ S" cannot be desribed as a formula. | Σ | is also sometimes very big. So, we should imagine that Σ is only a set of pairs (Y, z).
Based on the rewritten definition of "a set of closure rules", I made a figure that explains the three concepts are equivalent (i.e., Theorem 2.6).
(The following part was added on 27th Oct. 2017 (Japan time), after I consulted Dr. J.B. Nation on the topics of this page.)
Examples would be rewritten as
Maybe, you think that a set of closure rules as { (Y, z) : ... } are very similar to their descriptions in natural language. Mathematicians may easily convert the descriptions in natural language to the form of { (Y, z) : ... } in their brains unconciously and may regard the both forms equivalent.But they are different. Consider their cardinalities. The caridinality of the possible descriptions in natural language (more precisely, family of finite sets of (finite length) mathematical formulae) is ℵ0 (aleph0). On the other hands, the cardinality of the variations of closure rules, i.e., the cardinality of sets of closure rules (the collection of sets of pairs (Y, z)) can be bigger than ℵ0 (aleph0) depending on the cardinality of the set X.
It might be an interesting problem to think what kind of closure rules can be represented by first-order, or higher-order mathematical formulae. Of cource, all examples we can consider concretely should be described by finite formulae.
(end of addition)
was added, I would not be confused. Maybe my background knowledge from computer science, such as predicate logic, enhanced the confusing.a set of closure rules on a set X is simply a set Σ ⊆ P(X) × X
I know that I am only saying a poor defense. But, since I think some other people may be confused about the definition, I wrote this page.
This is the end of resolving the confusion.
Let's Study Lattice Theory (Japanese)