The Galois Connection between Syntax and Semantics by Peter Smith

(構文と意味の間のガロア接続)

についての紹介

この解説論文（チュートリアル）

Peter Smith : The Galois Connection between Syntax and Semantics
(PDF へのリンクです)

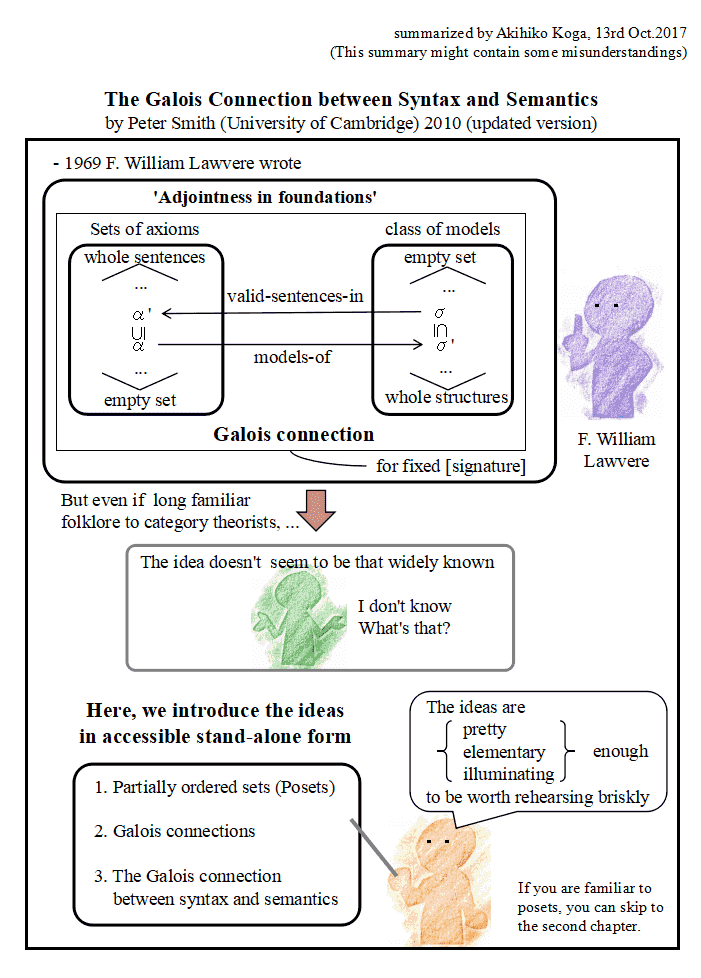
構文と意味の間のガロア接続の関係はもともと F. William Lawvere によって言われた みたいですがあまり広く知れ渡っていないとのことです．この論文は，Lawvere のアイデアを それ単独で読めるようにした入門書です．

この論文は Partially ordered sets (posets) の定義などは基礎的な部分から説明していますが， 数理論理学の基礎的な知識，特に形式論理の文 (sentence) とそれを解釈する構造 (structure) の定義に関する知識は予め必要なようです．この定義を知っていればこの論文は読むことができます．

なお，ガロア接続に関する簡単な解説を 順序集合や束などに関する基本的な概念の説明 に書きました．ご興味があれば．2021.03.06

Lawvere のアイデアの肝は，下の図の上部（Adjointness in foundationsと書いてある四角の中）のように，

• 論理式(sentence)の集合 α に対して，それを満たす解釈の集合 model-of(α) を対応させる写像 と
• 解釈の集合 σに対して，それらの解釈で成立するすべての論理式の集合 valid-sentences-in(σ) を割り当てる写像

第一章では Partially ordered sets (posets) の基礎が説明されます．この部分は もしすでにご存じでしたら，記法だけ確認して飛ばして構わないようです．

第二章でガロア接続の定義の後，５つの例が示されます．それらの中で例 (3)，つまり， 右側の poset が < {0}, = > のケース（唯一の要素からなる集合で ≤ は = としたもの）は，当たり前に見えますが，実はとても重要です． 実際，これは定理2.3.2

f^*(q) = the maximum of { p∈P | f_*(p) ⊑ q }

第三章では構文と意味の対応がガロア接続であるということから，色々な事実を導きます． それらの事実の中には trivial なものが多いので読者は若干落胆するかもしれません． しかし，ガロア接続であることを把握することにより，以前と比べて，構文全体の世界と意味全体の世界の 対応のイメージが明確になっているわけです．私は，数学的なものから組み立てられた 抽象的な「なにか」を生き生きとイメージする能力は，この分野の研究者にとって とても重要なことだと思います．

計算機科学においては，ガロア接続の重要な応用が色々あります．形式的概念分析 (Formal Concept Analysis) ，抽象的解釈 (abstract interpretation) などです．したがって この論文はそれらの応用のガロア接続への良い導入になります．

ガロア接続は圏論の随伴関手の特殊なケースになっていますので，ガロア接続を理解することは 圏論の学習の良い準備になります．実際，この著者 (Peter Smith) も彼のサイトで圏論の簡単なテキストを 公開していますが，そのテキストの中で随伴関手の前の導入にこの論文の題材を使っています． これについては

圏論のお勉強
(Let's study Category Theory)
Peter Smith 氏のテキスト紹介