"The Galois Connection between Syntax and Semantics
by Peter Smith"
Peter Smith : The Galois Connection between Syntax and Semantics
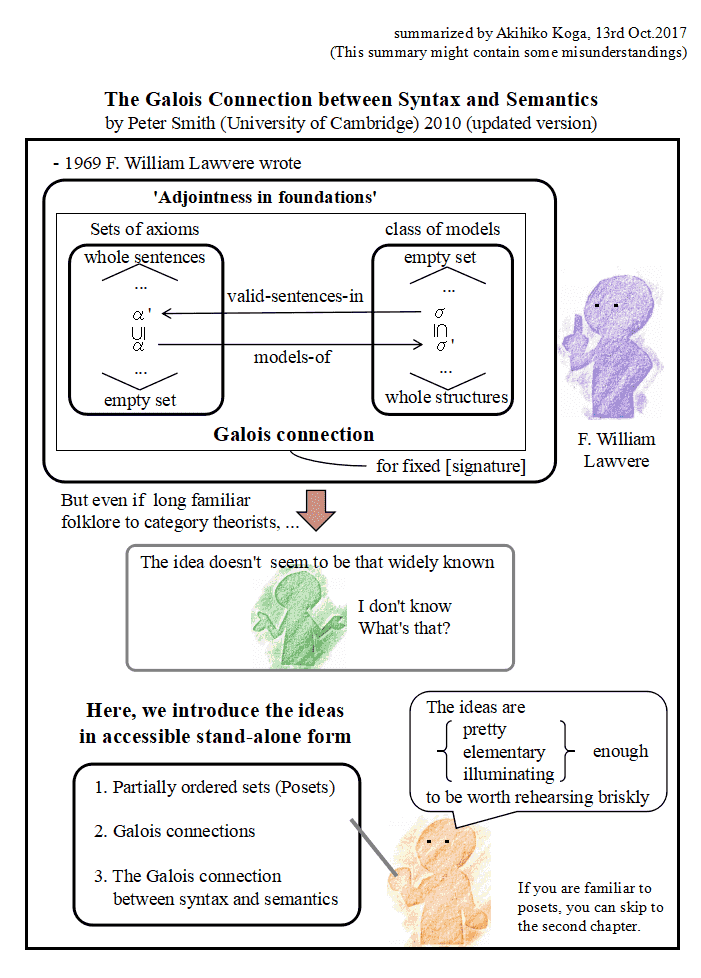
The relation between syntax and semantics was said by F. William Lawvere originally, but it is not widely known. This paper is an introduction to Lawvere's ideas in accessible stand-alone form.
Although this paper explains the Lawvere's ideas from the definition of partially ordered sets (posets), it requires readers the basic knowledge about formal logic, especially the definitions of sentences in formal logic and structures to interprete those sentences. If you know those two concepts, you can read this paper, maybe.
In the chapter 2, after the definition of Galois connection, 5 examples are shown. Among those examples, the example (3), i.e., the case in which the right poset is <{0}, => is basic and important while it seems trivial. Indeed, it is a special case of Theorem 2.3.2
f*(q) = the maximum of { p∈P | f*(p) ⊑ q }Examples (4) and (5) are important and interesting because they are examples from logic.
In the chapter 3, several facts are deduced as the results of Galois connection between syntax and semantics. Readers might encounter a little disappointing (trivial) ones among those facts. But, by means of Galois connection, now, we can grasp the whole image of the world of syntax and semantics clearer than ever. I think this ability to imagine an abstract 'something' built from mathematical objects vividly is very important for the researchers in this area.
Moreover, Galois connection has important applications in computer science such as formal concept analysys, abstract interpretation. So, this paper is also a good introduction to Galois connection of those applications.
Since Galois connection is a special case of adjointness in the category theory, understanding the Galois connection is a good preliminary work to the study of category theory. Indeed, the auther (Peter Smith) used the part of this paper as a preliminary chapter to the chapter of adjointness.
Let's Study Category Theory (English)
Let's Study Category Theory (Japanese)
Let's Study Lattice Theory (Japanese and on the construction)