Memo or Diary 03 Mr. K

他の日記へのリンク

丘浅次郎の「落第と退校」を読んで
- または「作文」のこと -

2020 年 10月 23 日 (金)

奥さんが亡くなった落ち込みからのリハビリプログラムの１つとして，青空文庫に挿絵を付けるコーナーに丘浅次郎（明治から昭和にかけての動物学者）の作品紹介の文書

落第と退校 (丘浅次郎著)

を書きました．

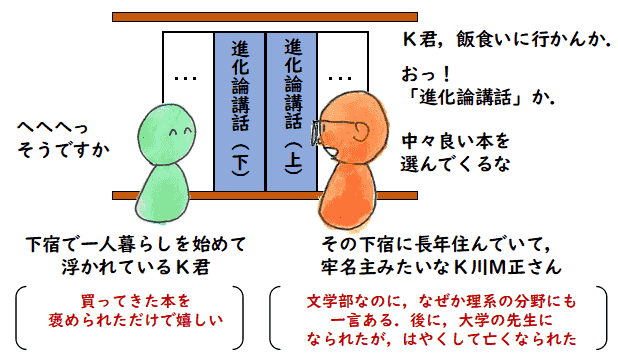
丘浅次郎は，「進化論講話（1904年）」という本を書いた人です．私が大学に入ったときに，本屋で講談社文庫の「進化論講話（上・下）（1976）」を買って，下宿に帰って読んでみると，えらく分かりやすい文章で感心したものでした．私が大学に入ったのは 1977年ですから，この本が最初に出た 1904 年からはずいぶんたっています．しかし，講談社文庫版が出たのが 1976 年ということは，私が，本屋で見たときは出てまだ１年なので，随分新しい本のように思ったのだと思います．

で，もとの作品「落第と退校」に戻って，この作品はタイトルからは分かりにくいのですが，当時の教育制度に対する批判です．旧来の価値観に縛られたり，満遍（まんべん）ない知識を持っていることを要求することで，才能の芽を摘んでしまっているということを言っているのだと思います．丘は，大学の予備門の入学試験に落ち，後にせっかく補欠試験で通ったのに，（年代を覚えるのが）嫌いな歴史の科目で二度落第して，退校になり，大学の正科に入学できず，撰科（せんか）に入ったそうです．これはその体験を思い出しつつの作品です．

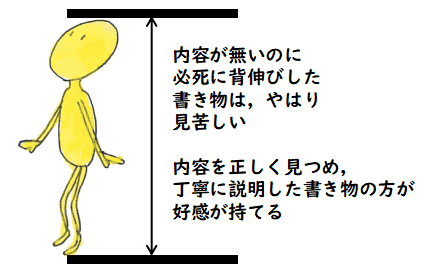
この作品で，丘は，当時の予備門や大学の制度に対して色々と不満を書いていますが，「作文」についても次の絵のような不満を書いています．

つまり，当時の作文では，なにか格調高く見える文章の書き方だけを教えていて，自分の考えをきちんと相手に伝える技術を教えていないと言っている訳です．

私は，この国語教育の傾向は私自身が育った時代も続いていたのではないかと考えています．

私の高校入学は 1974年なのですが，そのときに一気に国語が嫌いになりました．何か，訳の分からない文学作品の高尚そうな味わい方ばかり強調，かつ，強要されている気がしたのです．また，高校のとき，急速に理系の学問に惹かれていきましたので，余計，国語の勉強がおっくうになって，大学入試では，国語は100点満点中の30点くらいしかとれませんでした．当時，私が受けた大学は，何点以下の科目があったら不合格ということがありませんでしたので，他の科目でカバーしてなんとか通りました．

こういうことがあったのですが，一方，国語が出来なくてまったく問題ないと考えているかというと，そうではありません．国語の力不足は，それから延々と代償を払い続けているような気がします．国語にあまり時間を割かなかったので，丘浅次郎が言うところの

「自分の云ひたいと思ふことを、読む人によく解からせる様な文章を作る術」

もあまり力がついていないのです．おまけにどこで習ったんだか分かりませんが，文章を格調高くしようとして背伸びした表現になり，結局，分かりにくい，そして，内容の無い文章を書いてしまうという状態が長く続きました．我々，技術者も文書の読み書きで，技術の学習をし，そして自分が工夫して編み出した技術を相手に伝えている訳ですから，技術文書の読み書きが下手なひとは表の舞台に出ていきにくい訳です．

私が，技術文章を，

見栄を張らずに
読み手のことを考えながら

書く気持ちになったのは，大学院を卒業してからの会社生活においてです．だから，会社で，私の文章を見て注意してくれた人には感謝しています．もっとも，そういう気持ちになって，かつ，努力はしているというだけで，結果が伴っているかどうかは分かりません．また，今は，会社を辞めて自由にしているので，この日記みたいにわがままな書き方になって，ちょっと冗長な文章でも良いかとか，気が緩んでいるところもあるかもしれません．

上に書いたことは，高校から国語の授業をなまけた私自身の反省ですが，現在の教育で，きちんとした論理的な分かりやすい文書を書く技術が教えられているかと言うと，そうでもないのではないかなと思います．と言うのは，私は，とある大学でプログラミングの非常勤講師をしていますが，学生の中には結構しっかりしたレポートを書いてくるものもいるにはいるのですが，あまりしっかり書いて来ない学生も多いのです．高校までに，

「自分の云ひたいと思ふことを、読む人によく解からせる様な文章を作る術」

の練習をしていれば，もう少しましなのではないかと思います．

それで，今回は何が言いたかったかと言うと，技術文書の書き方も高校や大学でもう少しきちんと教育するようにしたら良いのじゃないだろうかということです．もちろん，人生を豊かにするには文章の味わい方も必要ですが，実際に社会で仕事をしていく上には，筋道だっていて，かつ，目的に合わせてコンパクトな文章を書くことが必要です．国語学習の半分はそのような技術の習得に宛てて，後の半分で，人生を豊かにする文章の味わい方を学習してはどうでしょう．そのとき，従来の国語の先生が，それを出来るかと言うと疑問です．彼らの多くは技術文書を日常的に，書いてもいないし読んでもいないはずです．そういう人たちに教育はできないでしょう．

ここまで書いてきて分かったのですが，要は，

こういう，人に分かりやすい文書の書き方が重要だという考えが不足している
したがって，それを教育する人員も不足している

ということが，明治から延々と続いているということではないでしょうか．

現在，世の中で動きがあるように，新しい教育で，プログラミングを教育することも重要でしょうが，私はそれより，きちんとした文書の書き方，読み方を教育することの方が重要だと思います．

最後に，もう一度，丘浅次郎の話に戻って，私が大学に入った時に感動した「進化論講話」が青空文庫でフリーでもう一度出ないかなと，ここ数年間，期待しているのですが，中々出ません．もう，入力は終わって校正待ちみたいなのですが，そこでずっと止まっています．で，この日記を書くのに色々検索をしていたら，

丘浅次郎進化論講話

というキーワードでググった１ページ目に，その入力したものを公開している人が出てきました．その人は，青空文庫で丘浅次郎の他の作品も入力した人です．丘浅次郎の著作権自身は切れているので，それを公開することは法に触れることではないと思います．青空文庫は，きちんと校正したものを載せたいので，校正が終わるまで公開されないのでしょうが，今，読みたいのなら，そこを読めば良いということが分かりました．図も入れて公開されているようです．リンクが切れると嫌なので，直接リンクは貼りませんが，現時点において上のキーワードの検索で探すことができるということを書いて，今回は終わりにします．

やはり大学に入ってすぐの出来事は結構覚えているものです．

比叡山の麓（ふもと）の田んぼだらけのところにある
賄（まかな）い無し，アパート形式，８室の下宿でした．
住民同士は結構行き来があり，食事時には，誘い合わせて，
近くの定食屋さんに出かけたりしてました

目次へ

YGU 氏のご冥福をお祈りいたします

2020 年 7月 31 日 (金)

今回は，某勉強会で知り合いになった YGU さんがお亡くなりになった話です．

「YGU さん」と伏字で書いていますから誰だか分かりにくいでしょうし，たとえ，実名が分かったとしても，YGU さんをご存じない方には何のことか分からないかもしれません．でも，後半は，私が YGU さんに触発されて，このコーナーに書き散らかした「AI とは何か」，「人間と機械の推論能力は違うのか」といったテーマの記事のリンク集になっており，ある程度，このテーマについて考える材料にはなると思います．

二週間ほど前に，私がこの２年くらい行いっていた勉強会のメンバー宛に，

その勉強会の設立者の YGU さんが突然亡くなられた

とのメールが，YGU さんの娘さんからありました．ご家族の方には心よりお悔やみを申し上げます．また，YGU さんのご冥福をお祈りいたします．

その勉強会は，どちらかというと数学や計算機科学を中心として，各自が興味のあるものを勉強してきて，二週間に一回，一人が２時間発表して３０分質疑応答があるというものです．各自が興味があるものということで，哲学，言語学，経済学，歴史，物理学，などなど多彩なトピックスがあります．なんでも，この会は，YGU さんたちが，某日本XXXSYS の時からやっている勉強会だったのだけど，メンバーの大部分が定年などで退職してしまったので，会も社外に出て，さらに社外のメンバーも加わって活動を続けているとのことです．すでに 468 回まで続いているのですごいものです． YGU さんは某日本XXXSYS の，もとお偉いさんで，G.H. ハーディの「ある数学者の生涯と弁明」という本の訳者でもあります．今，80歳台半ばだったと思います．その勉強会を取り仕切っていて，ご自身も一番多く発表されてました．

私は 2014 年頃，たまたま，その勉強会のホームページを見て，束論，論理学，圏論などの話題が時々出ているので，興味を持っていたのですが， 2017 年 12 月に，その会の KWB さんの「圏論による量子系のモデル化」というお話を聞きにいくために意を決して参加し，自分自身も計３回発表しました．ここの「メモのような日記のような」に，そのことをYGU さんも登場させて度々書いています．

その勉強会ですが，今は私は抜けています．というのは，私自身の話になりますが，今年の４月に妻が突然亡くなり，気落ちしてしまい，発表したり，議論したりする気力がなくなったからです．５月に，会の取りまとめの YGU さんに，「こういう次第でしばらく抜けます」と伝えると，そのことの了承と慰めの言葉をいただきました．それが，今度は YGU さん自身が亡くなられてしまいました．

娘さんのメールでは，世の中では，新型コロナウイルスによる肺炎が流行っているので，「葬儀などは家族のみで済ませる」と書かれていましたが，YGU さんは，もと日本XXXSYS の偉い人なので，やはり，旧知からの問い合わせなどで大変なのではないかと想像します．その大変な中に，せいぜい２年間の付き合いである私が加わり，余計な手間をかけてはと思いましたので，私は自宅で手を合わせるだけにしました．私自身，家内が亡くなったときの大変さを覚えていますし，実は，まだ色々な手続きが続いていたりするので，遺族に余計な手間を掛けさせたくないのです．

代わりと言ってはなんですが，ここの「メモのような日記のような」に時々出てくる YGU さん絡みのトピックスをまとめて，YGU さんをご存じの方々に YGU さんを思い出して頂く材料とすることで，私の供養とさせていただきたいと思います．

私と YGU さんとはこの２年間の勉強会だけの付き合いであり，また，私もあまり勉強会には出席していないので，たぶん，直接お話したのは１０回くらいと思います．したがって，ここでのお話はあくまで私がほんのちょっとのお付き合いの中で感じた少し偏見のある，私の「YGU さん像」ですが，単に「りっぱな人でした」というよりは，生の YGU さんのイメージを残せるのではないかと思いました．

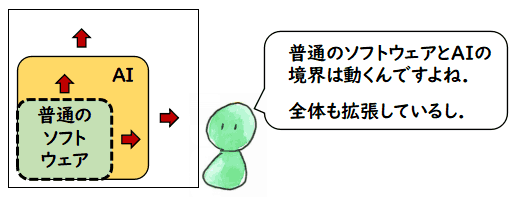
勉強会やその後の飲み会などで YGU さんと話した感じでは，私は YGU さんとは合わない部分が多いなと思いました．それはどこかというと，例えば，「人間は機械と違うのか，同じなのか」と言った問いへのアプローチに関してです．これらは，典型的には某勉強会で人工知能（AI : Artificial Intelligence）のことが議論されるときに出てきます．つまり，「AI とは何か？」，「普通のソフトウェアとどう違うのか？」に関してです．

私自身は，「人間と機械の能力は原理的には同じで，ただ，現状では規模が違うだけ」と考えています．つまり，どちらも帰納的関数，あるいは止まらない場合も許せば，帰納的列挙可能な関数です．YGU さんのお話を聞いていると，最初は私と同じかなと思うのですが，途中で，「うん？違うのかな？」というところが沢山でてくるのです．この二つに関する考え方の違いをまとめると

私と違い，たぶん，YGU さんは人間は機械にやれないことをやれると思っているような気がします．ただし， YGU さんの主張が

人間の能力 ≠ AI の能力 = 普通のソフトウェアの能力
なのか
人間の能力 ≠ AI の能力 ≠ 普通のソフトウェアの能力

なのかはよく分かりません．彼は，「AI が普通のソフトウェアと違うのは，センサーとアクチュエータを持っているところだ」とよく言われていました．私は
人間の能力 = AI の能力 = 普通のソフトウェアの能力

です．
YGU さんは，何か「もの」を考察するとき，厳密な定義から始めるという傾向が強いです．私もある程度はその傾向がありますが，そうまで拘りません．

となります．YGU さんは東大の数学科卒業ですし，私は落ちこぼれとは言え，某大学の数学科出身なので，上の２番目の項目，「定義を大事にする」気持ちは分かるのですが，人工知能など，厳密な定義が難しい分野に沢山関わってきたので，定義はブートストラップで次第に改善していってもよいし，なにか曖昧なまま残しておいても良いという諦めがあります． YGU さんは，その諦めの閾値がとても高いように感じました．

これらに関係して，ここの「メモのような日記のような」で YGU さんが登場する回を次に列挙しておきます．

循環定義を正当化する 2019 年 5月 9 日 (木)
これは私の知り合いの MTDA さんが「フレーム問題について」と題してこの会で発表したときの話です．MTDA さんの主張は，「深層学習が流行り，世の中ではフレーム問題が解決したかのような雰囲気があるが，ごく簡単なものが解決したに過ぎない．自然語理解などをやっていけば依然としてとしてフレーム問題は重要な問題である」ということだったと思います．

MTDA さんが大雑把に，自然語理解の文脈で，「意味」とか「理解」とかの語を自分の感覚に結び付けて話されるのに対して，YGU さんは，それらの語の定義をかなり強く求めていらっしゃいました．

そのとき，私が丁度，底の無い集合論（集合の要素を次々に辿っていっても底（集合以外のもの）にたどり着かない集合論）のことを調べていたので，このような無限に定義が遡（さかのぼ）れたり，あるいは循環している定義が可能ではないかという記事を書いてみたのです．
AI (Artificial Intelligence) とは何だろうか？トライアル 2019 年 12月 25 日 (水)
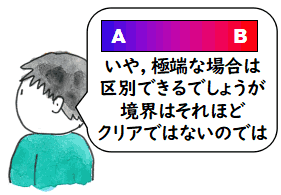
YGU さんが勉強会のスケジュールをメールでしているとき，私が「『AI とは？』というタイトルでパネル討論会を企画しては？」と提案したことがあります．というのも，勉強会の中で，時々，この話題が出て，YGU さんを含む数名が自分の主張をし始めるのですが，言葉のみで，資料がない議論なので議論が空回りするのです．次の絵の右側のコメントがこういう状況発生時の YGU さんのコメントです．

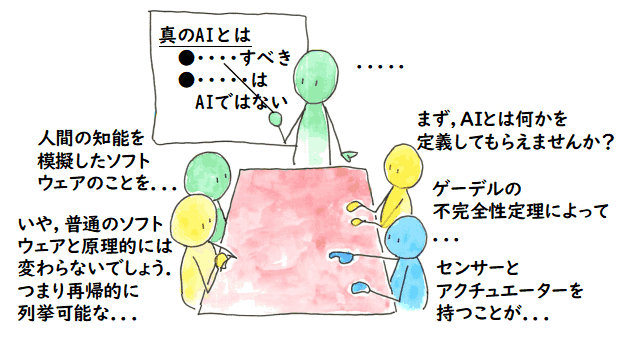
それで，私は，皆さんが資料を持ち寄って討論会をしたらどうかと提案したのです．このときは，私自身は聞く方に回り，話者の一人にはならないと言ったこともあり，この企画は実現しませんでした．この後，「やはり，自分は発表しないという態度は良くないのではないだろうか」と思い，ちょっと，このコーナーを使って自分の意見をまとめていたのです．それが上のリンクからたどれる記事です．これはゲーデルの不完全性定理などの内容を含んでいるので，少し長いです．

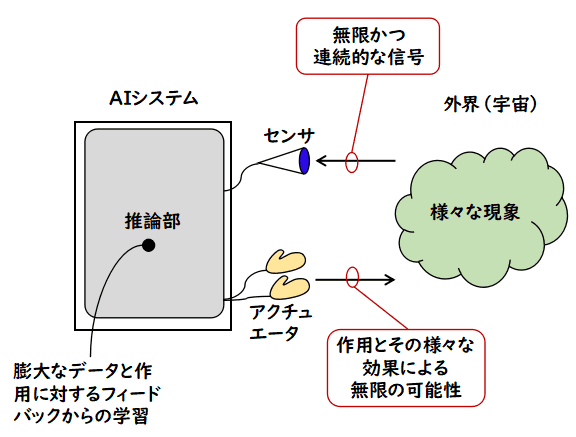
この絵は，YGU さんが良く言われる，
AI と普通のソフトウェアが違うところは，AI はセンサーとアクチュエーターが付いているところだ
を絵にしたものです．私は，YGU さんが何を意図しているのか正確には分かっていません．分からない部分のポイントは，YGU さんが，
ソフトウェアが，センサーとアクチュエータを備えることが，通常の帰納関数の能力を超えて機械では実現できない人間に近づく方法だと考えているのか，
あるいは
帰納関数の範囲内で高度なソフトウェアができると言っているのか
です．後者なら私は合意なのですが，何か話を聞いていると前者も混じっているような感じがするのです．尚，YGU さんは出てきませんが，この続編で，私自身も「人間 ≠ 機械」と考えている記事
機械と人間は違うか？ - A^* と A^∞ -

もあります．
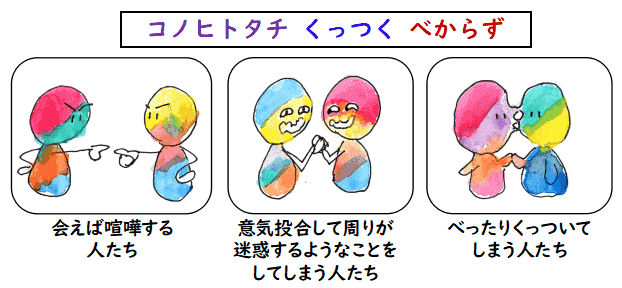
コノヒトタチくっつくべからず 2019 年 5月 26 日 (日)
この記事自体は，世の中に「このヒトタチつっつくべからず」という絵本があり，それを私は長い間「このヒトタチくっつくべからず」と思い込んでいたというお話なのですが，一つ前に書いたようにその勉強会で頻繁に

この絵のような状況が発生して，YGU さんを含めて結論のでない議論に突入するので，その場面では，私はいつも頭の中で，この絵本のタイトル
このヒトタチくっつくべからず
勉強会の皆さんは昔同じ会社にいて何十年もこういう議論を続けてきたんでしょうから，いい加減，相手の言うことを予想して，議論を避けるなり，逆に，深めるなりしてくれたら良いのに

のように悪態をついていました．
でも，もしかしたら，第三者が見るほど，このかみ合わない会話は当人たちにとってはつまらないものではないのかもしれません．延々と同じ会社でこういう議論を行ってきて，まだ，同じ勉強会にいるのですから．所謂，腐れ縁というものかもしれません．
計算機科学の発展を支える教育とは？ 2019 年 7月 11 日 (木)
これは勉強会の後の飲み会で，私が，
将来，圏論が計算機科学専攻の基礎的な素養になって，これを知らないと話にならないという時代がくるかもしれませんね
と言ったときの，YGU さんの反応です．

「そんな世の中には絶対なりません」と言われてしまいました．
でも，実は，これは私も分かります．世の中の計算機ソフトウェアは殆どが整数の加減乗除くらいの理論で作られているのです．
某勉強会で「計算機科学のための圏論の基礎の基礎」の発表をした話 2020 年 3月 28 日 (土)
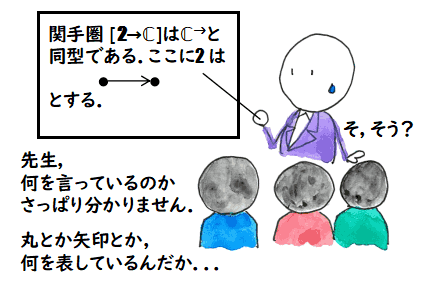
勉強会で，私が「圏論の基礎の基礎」と題して発表して，「我々，計算機科学の領域の人間が圏論を学習するとき，そこに現れる定義が何を意図しているかがさっぱり分からないことが多い」と言ったとき YGU さんは
いや，Kさんね，圏論に出てくる概念の意図が分からないというけど，あれはいくつかの数学的概念を横並びに見て抽象化したものだからもとの概念を思い浮かべれば...
と反応されました．

（正面が YGU さんです．絵が雑で申し訳ありません）

私は，そのとき，「あれらの定義が普通に頭の中に入ってくる人たちがいるんだな」と少し感動しました．
そのときは，一応，YGU さんに，
いや，YGU さんは大学で，抽象数学を立派に修めて卒業したのでしょうが，我々，抽象数学のバックグラウンドが無いものにとって，それら横並びにするものを思い浮かべることができないのですよ．

と言っておきました．でも，そのときはこの絵を見せなかったのが悔やまれます．

以上，ここのコーナーに書いたことから，YGU さんに関連することを色々並べてみました．ここだけ読むと，YGU さんはかなりの偏屈だと思われるかもしれませんが，たぶん，実際，そうです．同時に，私程度が太刀打ちできないくらいの成果を上げていますし，また，ご高齢になっても，学問の具体的な内容（形式だけでなく）まで立ち入った勉強をされている方でした．私なんかは，数学の定理でも，証明の概要さえ聞けば，自分でやってみようとは思わないのですが， YGU さんはきちんとそれも押さえていかれているようでした．勉強会の場でも，他の人のスライドの中の証明を一生懸命追いかけていらっしゃった姿を思い出します．

ちなみに，最初の絵

は，勉強会のホームページに出ている YGU さんの写真から，powerpoint で適当に図形を組み合わせてそれらしいアイコンを作ったものです．私のスマフォでは，gmail でYGU さんからのメールがあるとこれが出てきます．もう一つ，その勉強会のもう一人の大御所で YGU さんが敬意を払われていた YMSK さんのアイコンも

のように作成していました．

色々書きましたが，最後にもう一度，YGU さんのご冥福をお祈りいたします．

目次へ

束における分配不等式の３Ｄモデルのプロトタイプ
- 娑婆への復帰のためのリハビリ -

2020 年 5月 24 日 (日)

今回は束論の分配不等式の３Ｄモデルを作るお話です．

別の日記「私の奥様の朋子さんが突然亡くなられてしまいました」で書いたように，先月，奥様が急に亡くなってしまい，元気がでないというか，落ち込んでいました．しかし，いつまでも落ち込んでいる訳にも行かないので現世（娑婆）への復帰プログラムとして，ずっと放っておいたこの３Ｄモデルを作るというのに取り組んでみようと思った訳です．

分配不等式の３Ｄモデルは，ここの束論のページの

Distributive Inequality with Full points (Parallel view)

立体視の平行法で見てください

にあるのですが，実際に「物」を使って作ってみたり，CG を使って精細な画像を作ってみたりして，リアリティを向上しようという企みな訳です．

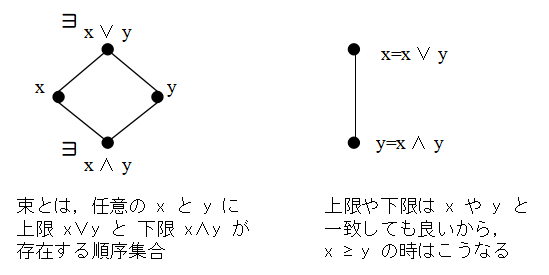
一応，束（lattice）の定義だけ言っておきます．

定義

（部分）順序集合 (L, ≤) が束であるとは，L の任意の２元 x, y に上限と下限が存在することである．

ここで，z∈L が x と y の上限であるとは，z が {u∈L | u≥x かつ u≥y} の最小元であること， w が x と y の下限であるとは，w が {u∈L | u≤x かつ u≤y} の最大元であることである．x と y の上限を x ∨ y, 下限を x ∧ y と書く．

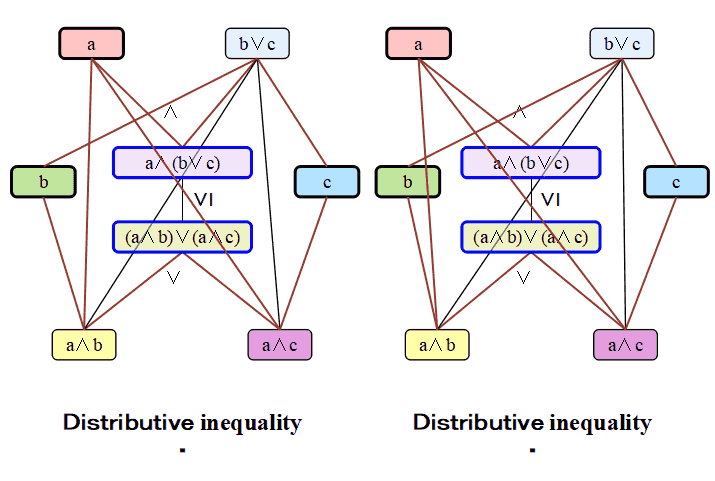
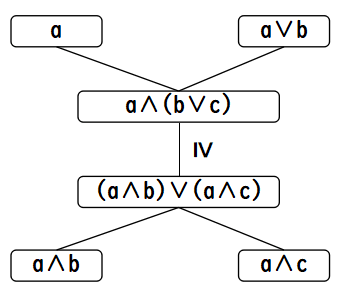
これも一応ですが，分配不等式とは

a ∧ (b ∨ c) ≥ (a ∧ b) ∨ (a ∧ c)

という不等式であり，束では常に成立します．この不等号が等号になっているのが分配法則

a ∧ (b ∨ c) = (a ∧ b) ∨ (a ∧ c)

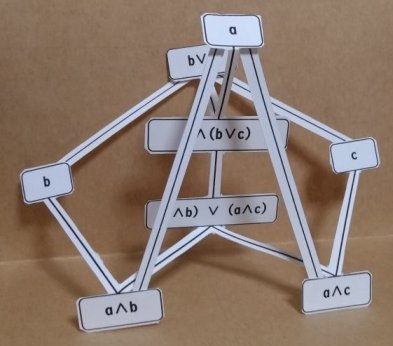
で，それが成り立つ束は分配束（distributive lattice）と呼ばれ，性質の良い束とされています．ブール代数は分配束です．でも，一般の束では，この等号は必ずしも成立せず，左の方が真に大きいことがあります．それを視覚的に表しているのが上のモデルの中心部にある次の部分です．

一般の束ではこの上下は一致するとは限りません．

で，今回，分配不等式の３Ｄモデルを作ろうとしてみて気付いたのは，

私がずっと放っておいたのは，実は，軸やノードとして適切な材料がなかなか見つからなかったという理由があった．気力がない今それらの解決が出来る訳がない

ということでした．一応は，石膏粘土と竹ひごとかで試してみたのですが，中々，きれいにできませんでした．

このまま放っておくと，また，長い期間寝かしてしまいかねないので，今回は，不格好でも，とりあえず，厚紙でペーパークラフトを作ってみました．

こんなのです．一応ステレオグラムの画像（平行法）も載せておきます．

スマフォを手で少しずらしながら撮ってみました．正確ではないですが，およそ立体が把握できるのではないかと思います．でも，やはり歪んでいるので長い間眺めるのは辛いですね．

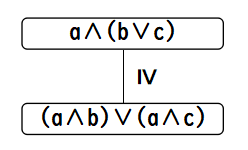
この分配不等式を把握するのに，本当に３Ｄモデルが要るかと言うと，重要な所は中心部分の

なので，必ずしも要らないのです．この図をどう読むかと言うと，

a ∧ (b ∨ c) は a ∧ b 以上です．
また，a ∧ (b ∨ c) は a ∧ c 以上でもあります．
(a ∧ b) ∨ (a ∧ c) は，a ∧ b 以上，かつ，a ∧ c 以上のものの中で最小元ですから，その二つの式以上である a ∧ (b ∨ c) 以下になる訳です．

ということで，分配不等式が成立することを見て取るためには，この３Ｄの大物ノモデルは要らないのですが，ただし，学習という観点からいうと，実際に工作してみて，単項の a, b, c も含めその中に出てくる式の間の位置関係を理解することは，この不等式に慣れるという意味で重要なことだと思います．

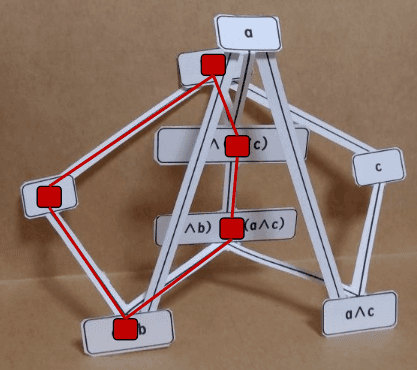
また，３Ｄモデルは次の図のように中に５角形を含んでいます．

この５角形はN5 と呼ばれる束で，

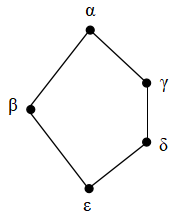
N5

モジュラー束（分配束より少し条件を緩めた束）になるためには，この N5 がその束の部分束として現れてはいけないという束です．単項の要素までモデルに含めるとそのこともしっかりモデルの中に現れてくる訳です．

こうやって，このモデルを作ったり，それを触ったりすることで，分配不等式に慣れることができます．多分，束論を習い始めた学習者は，この不等式に慣れたとしても，この不等式の意味が分かる訳ではないのですが，最初は

この不等式に登場する項（a, a ∧ b, ...）の関係が分からない
この不等式の意味が分からない

の二つの苦労があったものが，３Ｄモデルで慣れてしまえば，二つのうち一つの苦労がなくなるのです．その結果，意味の方に集中することができます．

上でもちらっと述べましたが，分配束の条件を少し緩和した束として「モジュラー束（modular lattice）」があります．それは，分配法則が常に成り立つわけでなく，c ≤ a の時だけ成り立つとするのです．つまり，

c ≤ a ならば a ∧ (b ∨ c) = (a ∧ b) ∨ (a ∧ c)

ここで， c ≤ a なら a ∧ c = c ですから，上の式は次のようになります．

c ≤ a ならば a ∧ (b ∨ c) = (a ∧ b) ∨ c

式は簡単になりましたが，意味はよく分からなくなりました．括弧が微妙に左右にずれても等号がなりたつ？分配束も何に役に立つのか分からないと言いましたが，分配法則自身は小学校の頃から

a*(b+c) = a*b + a*c

という式で慣らされているので，なんとなく役に立つ気がします．モジュラー束は慣れてないのでなんの役に立つのか一見わかりません．モジュラー束の代表的なものとしては，アーベル群の部分群がなす束があるそうです．これはデデキントが彼の研究 "algebra of modules" の中で発見したとのことです．まあ，具体例があり，役にはたっていたということですね．これらの不等式の意味を考えるというのは，いろいろな束で等式が成立するもの，しないものを見ていくことなんだと思います．

今回は紙で間に合わせに３Ｄモデルを作ったのですが，3D グラフィックスを使って作るのが，材料が不要で良いかなという気がしてきました．特にプラグインを必要とせず，ブラウザで見えるためには WebGL を使うというのが手ですかね．ただ，私はこれ，ほとんど知らないんですよね．ということで，この後のリハビリ候補として，WebGL とその上のライブラリ Three を学習して，分配不等式を可視化するというのが一つの候補としてありそうです．

目次へ

某勉強会で「計算機科学のための圏論の基礎の基礎」の発表をした話

2020 年 3月 28 日 (土)

先日，某勉強会で，「計算機科学のための圏論の基礎の基礎」と題して，圏論のチュートリアルのようなものを発表してきましたので，発表資料を

計算機科学のための圏論の基礎の基礎

に置いておきます．発表資料は枚数が 104 枚あり，時間も２時間喋りっぱなしだったので，終わり位には少し心が折れました．

全部のスライドに全く問題がないならまた違ってくるのかもしれませんが，今回のものは，自分自身の考えや感性をかなり入れていて，それが「十分伝わるかな？」とか「こんな反論があると怖いな」と思いつつ進めると，だんだん疲れが溜まってきて，１時間半くらいで心が折れ始めたのです．実は，こういうことはよくある事なのですが．また，気が張っていて，心が折れてることに気が付かない場合でも，次の日か，またその次の日に疲れが出ることはあります（ね？）．もっとも，今回は聞いてるほうも疲れたと思いますが．

私はこれから，なんとか，こういうチュートリアルをやって幾ばくかでも稼ぐことが出来たら良いなと思っているので，自分自身と聴衆の折れた心を伸ばす術も身に着けていかねばならないなと思うことしきりでした（まあ，当面は資料の改善と整備ですが）．

先日の発表では聴衆は８名，そのうちの２名の方は圏論を知っていて，それ以外の６名の方は自己申告では圏論を知らないと言われてました．勉強会の場を借りて，チュートリアルの試作品の初期テストをさせてもらったのでした．結果は，やはり，２時間ではあの 104 枚のスライドは喋り終えられないということでした．１時間45分でスライド 52 までしか行けませんでしたから，あとの 15 分は，残りに何が書いてあるかざっと概要を言って終わりにしました．チュートリアルの目的は，聴衆に理解してもらうことですから，やはり全部やろうと思うと４時間～６時間あった方が良いように思います．そうすると，長時間でまた自分の心が折れそうになるので，そこも鍛えたり，自分も聴衆も十分な休憩が取れるように時間割りを工夫したりが必要そうです．

今回の発表で印象的だったのが，聴衆の中の圏論をご存じの YG さんの次の発言でした．

K さんは圏論の諸概念の意味や意図が分かりにくいとおっしゃいますが，あれらは数学のいくつかの概念を横並びにして抽象化してみたものなので，それらを想像してみればその意味が分かってくるものなんです．

この発言の何が印象的だったかというと，

圏論の中の諸概念を別に難しいと感じていない人たちがいる

ということです．まあ，考えてみれば，圏論を作った人たちもそういう人たちだった訳でしょうから当然と言えば当然なのですが，自分がこれだけ理解に苦しんでいる中，直接，そういう発言を聞くと感動してしまいます．

今後，私自身は，当初からの目的

私のようになかなか圏論の学習が進まない（計算機科学の）学習者に，なんとか市販の教科書を読み進められるだけの動機の説明や，難しい概念の紐解きをした教材を用意する

に向かって進もうと思っています．とりあえず，今回作ったものは，「自然変換」さえも含まないくらい，圏論に必要な概念が不足しているものですので，そういうものの説明の資料を書いていくことが当面の仕事かなと思っています．

あと，こうやって仮想的な聴衆を仮定して，説明資料を作るという作業は自分自身の勉強にもすごく役に立ちます．自分自身があやふやだった部分をすべて明確にしていかなければならないのですから．

目次へ

<ul> と <ol> の上のスペースがなかなか取り除けなかった話

2020 年 3月 26 日 (木)

長めの話が続いているので，ここらで短いのを一つ書いておきます．とは言いつつ，html のタグの話なので，興味のある人は少ないと思いますが．

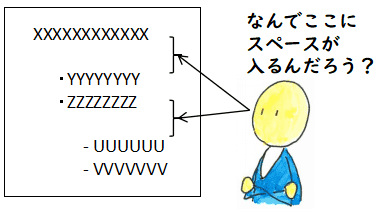
先日，某勉強会で，圏論のチュートリアルのようなものを発表してきたので，こちらのサイトにも載せることにしました（計算機科学のための圏論の基礎の基礎）．そのとき，某勉強会に送っておいた内容梗概をこちらに html の形に修正して載せようとしたのですが，次のようにどうしてもリストの上に意図しないスペースが空いてしまいます（「圏論の計算機応用に関する概要」の上と「代数/余代数によるデータ型の表現」の上）．

今回は，そのパイロット版として

圏論の計算機応用に関する概要　　
圏論の基礎的な概念の解説
応用の雰囲気が分かる題材の紹介
- 代数/余代数によるデータ型の表現　　　　　
- デカルト閉圏（CCC）による型付きλ計算の解釈

を含んだものを試作しているので紹介したい．

この html のソースファイルは

  <ul>
　　<li>圏論の計算機応用に関する概要
　　　　...
     <ul>
　　　　<li>代数/余代数によるデータ型の表現
          ...

で，今までもこの形で使っていたのに，今回だけこんなに大きくスペースが開くのはなんでだろうとと思いながら，インターネットを検索して，スタイルシートを margin-top:0px; とか padding-top:0px; とか色々ためしてみましたが，一向にスペースはなくなりません．

で，一日悩んでやっと分かりました．某勉強会に送ったテキストでは，テキストによる整形をしていて，各項目の前に全角の空白を入れてインデントしていたのです．そのテキストに <ul> や <li> を挿入していたので，全角の空白を■と書くと次のようになっていたのです．

  <ul>
■■<li>圏論の計算機応用に関する概要
　　　　...
     <ul>
■■■■<li>代数/余代数によるデータ型の表現
          ...

これでリストの最初の項目の上に■■や■■■■が一行取られて表示されていた訳です．つまり，全角の空白を■で明示すると，次のように表示されていたわけです．

今回は，そのパイロット版として

圏論の計算機応用に関する概要 ■■
圏論の基礎的な概念の解説 ■■
応用の雰囲気が分かる題材の紹介
- 代数/余代数によるデータ型の表現 ■■■■
- デカルト閉圏（CCC）による型付きλ計算の解釈

を含んだものを試作しているので紹介したい．

まあ，これらを半角のスペースに変えることで，余計なスペースが無くなって，事なきを得たのですが，見えない文字は厄介だったというお話でした．

目次へ

「やはり基礎はとても大切！」というお話とちょっとだけ圏論のお話

2020 年 2月 27 日 (木)

前回の記事「川を渡って良いものか？」で，大学の先生は「基礎的な教科書や教材を作成すること」に関しては，

自分自身は何がどう難しいかを忘れてしまったり，あるいは，最初から簡単に理解できたので何が難しいか分からないとしても，自分の周りに，分からない学生が常にいるので，彼らからその分からなさを教えて貰える恵まれた環境にある

ということを書きました．

実は，もう一つ，大学の先生方が恵まれた環境にあると思うことがあります．それは，

否応なく，毎年，繰り返し繰り返し，基礎をやらなければならないこと

です．これは別に，教科書や教材を作ることに関して恵まれているという訳でなく，先生方自身の勉強に関して恵まれているという意味です．

一般に，基礎はとっても大切です．私が非常勤講師で教えに行っている科目は，数学ではなく， C言語の応用編みたいなものですが，そこでの分からない学生は，応用編が分からないのではなく，その前の基礎編でつまづいている学生が多いのです．

学生は応用編の単位を取らないといけないので，労力をその前の基礎編の復習に向ける気が起こりません．なんとか基礎編の復習をせずに，応用編の課題を解けないかと頑張ります．教える側の私としては彼らの基礎編の知識の欠落状態が分かるので，一応は，「君は基礎のこの部分が分かってないので，昔の教科書を見て復習してごらん」とは言うのですが，彼らの

「そんなことをやっている暇はない」

という反論にあってしまいます．「足場かけ（scaffolding）」で届く場合はよいのでしょうが，足場を作れないほど基礎ができていないときは，やはり，基礎を固めなおさなければ，かえって時間がかかったり，あるいは，達成が不可能になってしまいます．

話を，「大学の先生が毎年基礎を繰り返さなければならない恵まれた環境にいる」ということに戻しますと，この基礎が大切というのは，なにも学生さんたちだけに限ったことでは無いと思います．私は非常勤講師で担当しているのは，このC言語の応用編だけなのですが，年に２回，説明資料を見直して改良していきます．

また，扱っているプログラムに関しても色々な実験をしてみます．そうするといろいろな疑問が出てきて，それをC言語の規格書で調べなおしたり，あるいはプログラムを色々な条件で走らせて実行速度などのデータを収集・整理してみたりします．扱う対象はごくごく単純なプログラムなのですが，結構，自分の知識の空隙が見つかったり，新たな発見があることがあります．また，同じ表記や同じ課題に何度も触れるので，それらを把握するのにほとんど頭の中のリソースを使わなくなるまで習熟していきます．これは，一つの見方を固定させてしまう危険性はあるので気を付けないといけないのですが，しかし，大部分の場合，頭の中のリソースを真に思考力を必要とする対象に向ける余裕を生みます．

以上のような理由から，基礎を何度も繰り返すということは，自分自身（先生自身）の勉強にも役立っているなと思うようになってきました．もし，非常勤講師でこの科目を受け持ってなかったら，馬鹿らしくて C言語の基礎なんかやらないと思います．これを受け持っているので仕方なく，年に２回，ここ数年間にわたって， C言語の基礎を復習し，いわば，過剰に学習しているような状態になっているのですが，やってみて思うのは，別に「過剰」なことはなく，普通に役にたっているということです．このようなトレーニングを，お金をもらいながらやらせていただけるのはとてもありがたいです．本職の先生方はもっとこういう機会に恵まれる訳です．もっとも雑用も多そうですが．

ちょっと想像してみると，数学とかでも同じじゃないかなと思います．研究の第一線で活躍している著名な先生でも，大学で１年生や２年生の授業を持っている場合は，例えば，線形代数や初等群論の授業を毎年行うことになります．そこでは，毎年，かわいい学生のために授業を見直したりしているでしょう．群論の初等的な定理を学生の前で毎年証明してみて，少しでも分かりやすいように証明を構造化したり，説明を工夫したりしていると思います．それらの作業は，自分自身に対しても，証明を徹底的に理解したり，また，それを他人にとても分かりやすく説明するトレーニングなっていると思います．

特に，この「分かりやすく説明できるようになる」というのは重要だと思います．よく，

自分では分かってはいるんだけど，それをどうやって人に説明して良いか難しい

という人がいますが，説明できないということは，「分かっていない」か，あるいは，「十分には分かっていない」ことが多いのではないでしょうか．

本当に口下手で，分かっているけど説明できないという人もいるとは思いますが，多くの場合，口に出してみるとつっかえるということは，把握している概念が十分繋がっていないということじゃないかという気がします．あるいは，それらがうまく繋がるようになると，今より良く理解できた状態になるとか．

以上，大学教育におけるプログラミングや基礎数学の例をみてきましたが，これらの知見を（計算機科学で使うための）圏論の学習に役立てられないか考えてみます．圏論の学習では次のような所でつまづいたと感じる人が多いのではないだろうかと思います．

米田のレンマ (the Yoneda lemma)
随伴関手（adjoints）
モナド（monads）
（もしかしたら冪オブジェクト（exponentials）も）
（もしかしたら極限，余極限（limits, colimits）も）

注）S. Awodey の Category Theory に載っている項目を参考にしましたので，比較的基本的な項目だけ拾っています．

でも，実際にはそれらの人はその前につまづいているのではないでしょうか？たぶん，自然変換 (natural transformation) あたりから，モヤモヤとしたものが溜まっていって... ．でも，なんとなくわかったつもりになって進めていって，とうとう上のような項目の学習で「もう，先に進めない」という気持ちになるのではないかと思います（これは実は私のことです）．

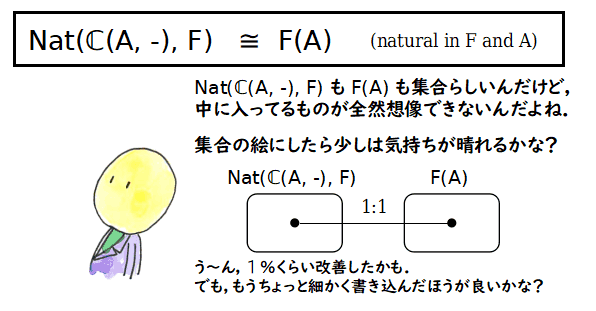
上にあげた項目の中で，例えば，米田のレンマは，表現可能関手 C(A, -) : C → Set と任意の関手 F : C → Set との間の自然変換の集合 Nat(C(A, -), F) と集合 F(A) の自然な同型に関する命題です．したがって，自然変換があまり分かってないと，この命題自身を想像することができません．また，そこでの同型は「自然」であるという但し書きがついていますので，ここでも「自然」ということが重要になります．

ここは勇気をもって，もう一度自然変換の章に戻ってみることが必要なのでしょう．

自然変換が分かるためには関手 (functor) が分かっていなければなりません．もし，自然変換がどうしても分からなければ，関手の章に戻って，関手の例を色々みたり，関手にどんな意味付けが可能かなと考えてみるのが良いのかなと思います．自然変換は，そこで関手に意味づけたものの間の準同型（構造を保った変換）みたいなものになっているのでしょう．

さらにもっと前に戻って，始対象や終対象を復習したり，また，見方を変えたら，こういうものが始対象や終対象としてみることができるなどの考察をしてみるのも良いと思います．基本的に始対象は最小値で，終対象は最大値です．ある問題の一般解の最適な表現を求めようとするとき，その問題の条件を満たすオブジェクト，あるいは，何らかの構成物を集めて圏を作れば，求める一般解の表現は，その圏の中の最小値，あるいは，最大値として定式化できる可能性があります．

もし，手元の本では，そのような概念の説明が十分でなかったり，例が少なかったりした場合は，別の本やインターネットで公開されているチュートリアルの類を調べてみるのも良いと思います．最近は，自分の講義資料を CC (Creative Commons) の著作権で，ホームページやarxiv に公開している大学の先生方が結構いらっしゃいます．

基礎の繰り返しの学習は，その後ずっと効果が続きますから，その後の項目数を N とすると ×N で効いてきます．N 倍化です．ですから，これがプラスに効いてくる場合と，授業の担当のように，お金をもらうかわりのオブリゲーションという場合はずっと基礎をやってたら良いのではないでしょうか．

P.S.

来月の終わり位に某勉強会で圏論のごく基礎の発表をすることにしましたので，発表資料の作成を始めました．本当にごく基礎の部分で，たぶん，自然変換も含まれません．発表資料は先方のホームページに公開されますが，発表が終わったら，こちらのサイトにも置くかもしれません．

目次へ

川を渡って良いものか？

2020 年 2月 14 日 (金)

以前，「ソフトウェア科学とボサツ様」で

ソフトウェア科学のあちら側（理論的な世界，抽象数学的な世界）に容易に行けるような教材作り

に興味があると書きました．

そのような教材を作るためには，自分自身，あちら側に行かないといけないのですが，安易に行ってしまって良いのだろうかという心配があります．私は，今，こちら側にいるのであちら側に行くのがいかに大変か分かるのですが，「あちら側に行ってしまったら，それが分からなくなるのではないだろうか」という心配です．

大学で代数や代数幾何など高度に抽象的な数学を専攻した人たちには分からないかもしれませんが，理系でも別の畑で育った人間には抽象数学はかなり分かりにくいものです．私は，何かの気の迷いで，圏論を使った計算機科学の論文を読んでみることがありますが，読み始めるとすぐに頭がくらっとして，しばしば次の絵のように抽象数学の波に翻弄されている幻想に襲われます．

( 半群論のページの絵を描きなおしました）

たぶん，数学を専攻していても，解析学など比較的現実への応用のある分野の方はこのように感じる方がある程度いるのではないでしょうか．

私は数年前，会社を辞めた時，仕事をしながらこういう抽象数学を学習することの辛さを知っているので，これからは，ここの橋渡しをするような活動をしていこうと思いました．つまり，大学の初年程度の数学が分かる人に対して，計算機科学で使うような圏論や束論など，抽象数学の習得を助ける教材を作ったり，勉強会を開いたりすることです．そして，その延長上に小遣い程度でもよいので幾ばくかのお金を稼ぐことができれば嬉しいなと考えています．なにしろ，それらが「分からない」という感覚を知っているのは，それらの分野で活躍している先生や研究者に対する私のアドバンテージな訳です．彼らは「『分からなさ』を分からない」ので初心者に優しい教科書は書くことができないはずです．

そこで最初に書いた「心配」が出てくるわけです．

あちら側（that side）に渡っても「分からなさ」を分かっていられるか？

どうなんでしょう？　もともと分かっていなかったという事実があるのですから，それを覚えていられるかもしれません．でも，「何が分かっていなかった」という項目は覚えていられるかもしれませんが，それはあくまで項目であり，変質してしまった知識なので，生の「分からなさ」ではないかもしれません．あるいは，何が難しかったかを全く忘れてしまうかもしれません．こうなると私が唯一持っているアドバンテージを捨てることになります．

こういうことを色々悩んでいたのですが，最近は，「たぶん，「分からなさ」は忘れてしまうんだろうな」と思うようになりました．私はある大学でC言語の応用編のような教科の非常勤講師をしていますが，コマンド引数の扱いの章で，「分からない」という学生が時々います．それは，C 言語の main()

    int main(int argc, char *argv[])
    {
        /* argv[i] を使ってコマンド引数の
           判断や処理をする */
    }

で，実行時に与えられたコマンド引数 argv[i] の判断や処理を行うという課題なのですが， argv[i] がコマンドの i 番目の引数として与えられた文字列ということがなかなか理解できない学生がいるのです．

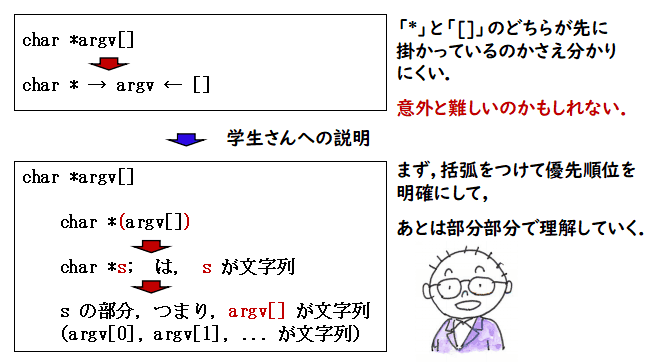
「char *argv[] が何のことなのかさっぱり分かりません」という質問を最初に受けたときは

えー？文字列の配列でしょう．何か悩む要素はあるの？

と思ったのですが，よくよく考えてみると，これはパラメータ argv の両側から「*」と「[]」が掛かっている訳で，なかなか分かりにくいのかもしれません．しかも優先順位も明示されていないので，どちらが先に掛かっているのかも分からないのでしょう．思い返してみると，私も C言語を学習しているときは悩んだのかもしれません．こう考えて，学生さんには次の図のように優先順位から丁寧に説明していきます．

上の例では，要素に分解するまでもなく，我々は，

    char *array[];

で，すでにパターンが頭の中にできているので，難なく読み取れるわけです．ものを勉強していくとこういうパターンは頭の中に沢山できてきます．そういう人たちには，部分部分を定義に従って組み立てていくしかない初心者の苦労は分からないのだと思います．

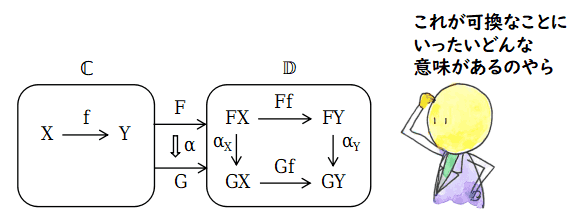
多くの圏論の書き物で，次のようなモナド（monad）の可換図式がさらっと出てきます．

最初にこれを見た学習者がこの内容をくみ取るのはとても大変だと思います（私は今でも大変です）．特に，自然変換と関手の合成をきちんと勉強してきていない人にとっては意味を解釈することさえ出来ないかもしれません．でも，ある程度慣れて，こういうパターンが頭の中に刻み込まれてくると，その大変さが分からなくなってしまうのでしょう．上の char *argv[] と同じです．教科書を書いている人は，その段階では，一瞬でこれを読み取れるのです．ただ，落ちこぼれる人の比率は char *argv[] より高いと思います．

上の二つは，「以前は分からなかったということ」が分からなくなる例でした．人間はその時々の状態で，以前の気持ちや思考過程を忘れてしまうことは，こういう例を出さなくても，プログラマならよく経験していると思います．昔書いたプログラムの中の文の意図がどうしても分からないということはよくあることです．「明日の自分は他人」なのです．きちんと，プログラム作成の rationale （合理的理由，根拠）は残していかないといけないのです．

こういうことを考えると，やはり，

何が難しかったか
どうやって克服したか

のようなことは極力残していかないといけないのでしょう．これらを残していったとしても，自分がすでに変質してしまっているので，知識としてしか残ってはいかないのでしょうが，何も残さないよりはましです．

もうひとつ，上の学生の例を書いていて思ったのですが，近くに分からない初心者がいるということはありがたいことです．自分が，「分からないところがどこか」分からなくなっても，その初心者が教えてくれるからです．

今作成しようとしている教材に関して，学校で教科を持っている訳でもない私が，このような状況を作ろうとすると，常に初心者を確保して，うまくフィードバックを受ける方法を考えなければなりません．作ってみた教材で，あまりクレームの入らない条件を設定して，時々勉強会でも開いてみるのは良い手かもしれません．

以上をまとめると，今回の結論としては，次のような感じでしょうか．

「分かりにくさ」は忘れるだろう
ある分野の初心者用の教材を作ろうとして，勉強していった場合，やはり，「分からない」という気持ちを保持し続けることは難しいと予想される．
考えられる対策は記録を残していくこと
したがって，初心者がつまづくところを十分ケアした教材を作るためには，勉強の途中で，時間がかかっても，極力，
- どこが分からなかったか
- どうやって解決したか
を残していくしかない．
教材は継続的に改善することが重要
「分からにくさ」を知るためには，出来上がった教材を初心者に説明してみて，分かりにくい部分はどこかを聞く環境を整えることが重要

まあ，すごく当たり前な結論ですね．ということで，「川を渡る」ことにしますが，あとは本当に渡り切れるかどうかがとても心配です :-) ．

P.S.

最初に，「『分からない』気持ちが分かることが私の唯一のアドバンテージ」と言いましたが，大学の先生は，多くの分からない学生を抱えているので，教育熱心な先生なら，このアドバンテージを学生から貰える環境にあると思います．そうすると私のアドバンテージはもともと無いことになってしまいます．まあ，『分からない』気持ちを強く意識する態度位ならまだアドバンテージとして残っているかもしれません．

目次へ

機械と人間は違うか？ - A^* と A^∞ -

2020 年 1月 15 日 (水)

今回のお話は，以前（2019年12月25日）のメモ「AI (Artificial Intelligence) とは何だろうか？トライアル」の続きです．私は，そこで，

機械ができないことを人間が出来るとは考えない

と書きましたが，今回はそれの逆に見えることを書きます．

期間的には前回から１か月もたってないのですが，まあ，年が変わったということを言い訳にして，今回は逆のことを書きます．前回のお話はとっても長かったのですが，できれば前回の話もお読みいただけると今回の話の位置づけが明確になるかなと思います．

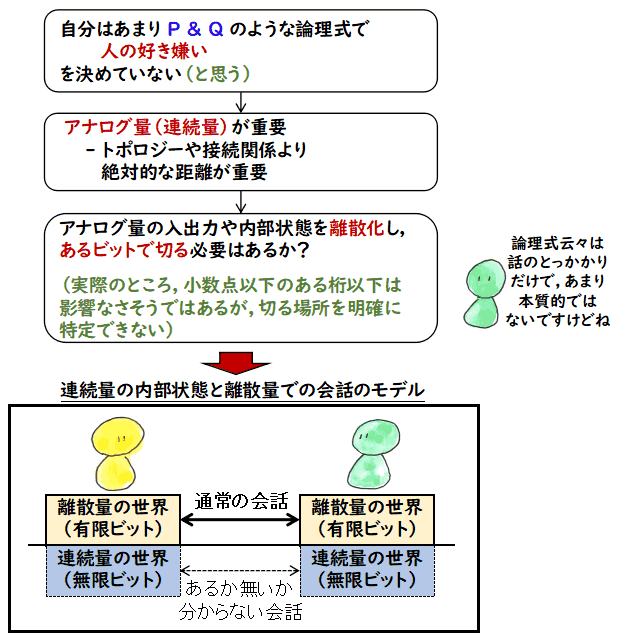
話をひっくり返すことになった切っ掛けは月並みなのですが，上の絵のような状況を考えたとき，

自分はあまり論理で人の好き嫌いを決めてない

と思ったことです．どちらかというと顔から受ける印象で好き嫌いが決まっているのであって，

(P1 かつ P2) または
((任意の x に対して P3(x, y) を満たす y が存在するならば P4) かつ ...) または
...

というような論理式では決めてないなという気がしています．もちろん，顔の印象も論理式だという論もあるでしょうが，素朴なアイデアとしてはアナログ量で決めているように思うのです．

実際的にはある量以下の微細な量については認識できず，有限の桁数で打ち切った「好き嫌い判定処理」をしても問題ないのでしょうが，どこで打ち切るという明確な基準が無い以上，連続量をどこかで打ち切ることは近似をとっていることになります．そのようなことを考えていくと，これも月並みかもしれませんが，上の絵の一番下の「連続量の内部状態と離散量での会話のモデル」に行きつきます．こういうイメージにたどり着いてしまうと，重要なのは連続量に関する述語を扱えることであって，それらを使って論理式を組み立てれば良いので，論理式云々というのはあまり話の本質ではなかったかなという気がします．

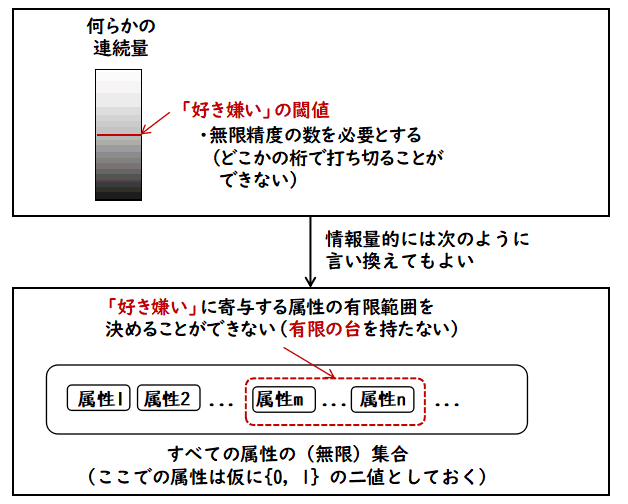
一つの連続量に限って言うと，「どこまでも精度を求めても仕方がないじゃないか」という気になりますが，次の図のように，閾値を無限精度で決めるということは，情報量的には，無限の二値の属性の中から，「好き嫌い」に関する属性の有限集合（有限の台）を決めることにほかなりません．要は，「好き嫌い」に関する有限個の属性を特定できるかという問いに何らかの答えを返す必要があります．

今まで，実数 v.s. 有限小数のような対立で表現してきました．有限小数側では 1/3 = 0.3333... のような数も容易に扱い得る数なので，実数 v.s. 有理数と言い換えてもよいかもしれません．有理数は有限桁の整数 n, m を使って，n/m と表現できる数です．

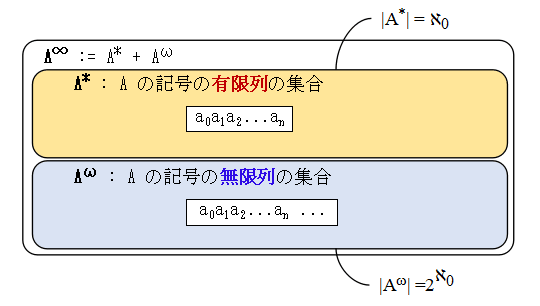
ゲーデルの不完全性定理の中に現れるゲーデル数もそうですが，我々が日常扱っている事柄を数で表現するのは分かりにくいものがあります．計算機科学が発達した現在は，数より分かりやすい体系があります．それは文字列です．簡単に用語を定義しておきます．

A : アルファベット．文字列を組み立てる記号の集合．ここでは A は有限集合としておきます．
A^* : A の記号の有限列の集合．ここでは長さ 0 の列も含めておきます．
A^ω : A の記号の無限列の集合．
A^∞ : A^* と A^ω を合わせたもの．つまり， A^∞ := A^* + A^ω

A^* は基本中の基本ですから計算機科学を専攻している方はよくご存じでしょうが， A^ω や A^∞ は余り出てこないのでご存じない人もあると思います．A^* は無限個の要素からなりますが，その基数は ℵ₀ で，自然数の集合と同じ大きさです．それに対して，A^ω は 2^ℵ₀ で実数の集合と同じ大きさであり，A^* より遥かに巨大です．

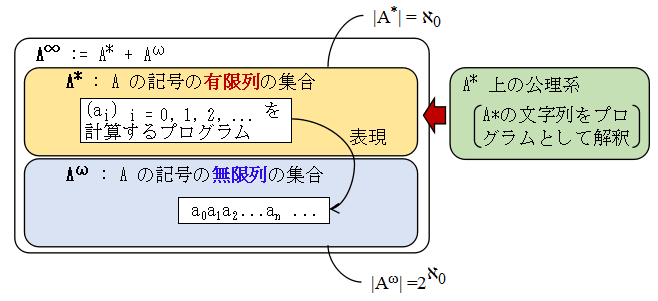
もう一つ言っておくことがあります．A^* は結構表現能力が高く，A^ω の一部分の要素を表現することができます．というのは，A^* はちょっとした公理系を導入すると再帰関数を定義するためのプログラミング言語として使うことができます．この言語を使って，無限列 (a_i) i = 0, 1, 2, ... を i に対して計算する再帰関数を定義すればよいのです．この A^* の要素を使って，(a_i) i = 0, 1, 2, ... を表現すれば，本来無限列となり有限の文字列では表現できなかったものが，A^* の中の有限の文字列で表現できることになります．もちろん，全部は表現できません．|A^ω| の方が |A^*| より遥かに大きいわけですから，表現できるのはほんの僅かです．

この A^* の有限長文字列で A^ω の一部分を表現できるという性質は，我々が円周率 π や自然対数の底 e などの無理数を有限の記述で表現できることを考えると分かりやすいでしょう．実数すべての集合は 2^ℵ₀ の大きさがあり，その要素すべてが有限文字列の表現を持つという訳ではありませんが（すべての有限文字列の集合は ℵ₀ のサイズ），一部は有限文字列の表現を持ちます．π や e などは無限に続く桁を計算し続ける再帰関数があり，我々は，日常，有限長の言語によってそれらの数を扱うことができています．まあ，各桁を計算する再帰関数まで持ち出さなくても，それらの数は，もともと定義が有限長の文字列でできていますね．

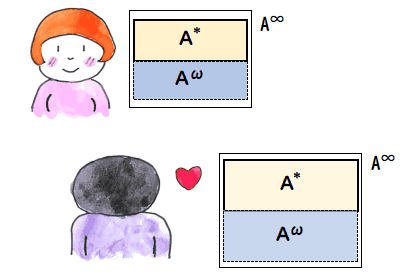
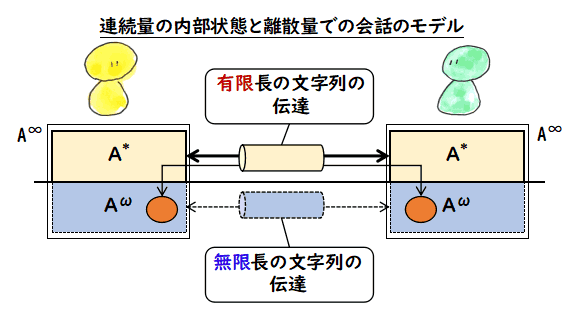
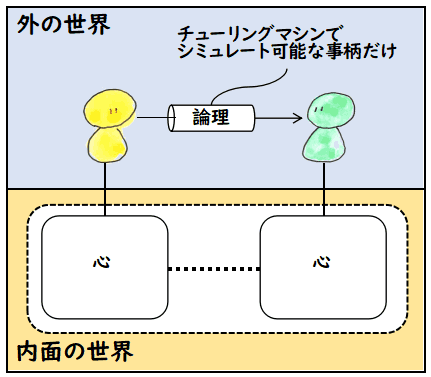
これらの用語を使うと「連続量の内部状態と離散量での会話のモデル」は，次のように書き表せます．

このモデルは，

我々が持っている伝達手段は A^*，つまり，有限長の文に限られるため，人は自分に内在する A^ω の要素を伝えようとするのだけど，それは A^* で表現できる要素に限られ，発話した瞬間に内在したものとの差異を感じて，何度も何度も言いなおす．

とか，我々が時々経験する議論でのもどかしさを説明してくれているかもしれません．本当に A^ω 間の伝達が可能なら，真に分かりあえたと言えるのでしょう．

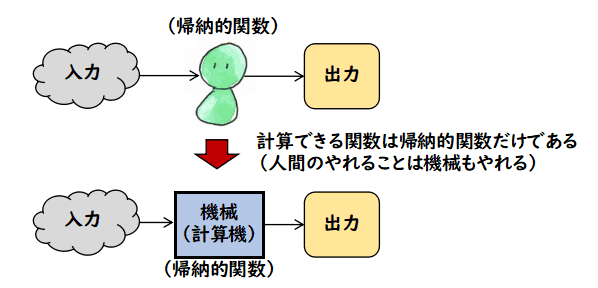
このモデルはチャーチのテーゼを理解するのにも役に立ちます．

チャーチのテーゼ
計算できる関数は帰納的関数だけである

このテーゼの文言で，「計算できる」は「機械が計算できる」という限定はなく，「人間が計算できる」も対象に入っています．

人間や機械の間を A^* で伝達している以上，有限の長さの文字列で伝達されるものを表さなければならず，それは有限の長さのルールで計算できるものに限られる訳です．したがって，伝達手段を A^* に限定している以上，チャーチのテーゼは成り立たざるを得ません．

年末，KNDH さんとお話したとき，彼は

「チャーチのテーゼは経験則である，つまり，まだこれに反する例を我々が見つけ出していないもの」

と言われていましたが，私は，

「陰に A^* での情報伝達を仮定した下での不可避な結論」

という気がしています．もう一度，双方が元気なときに，お茶でもしながら議論してみようかと思います．

KNDH さんとのお茶会のイメージ図

ちなみに，A^ω の要素 (a_i)_{i=0, 1, 2, ...} は A_i = A としたとき，A_i から要素を一つずつ取ってくる選択関数です．選択関数 f(i) := a （定数）と言った有限文字列で表現できる，つまり，A^* で表現できる選択関数もあれば，そうでないもの，つまり選択の基準を明確に与えられないものもあり，後者の方が圧倒的に多いのです．例えば，A_i を何らかの述語で P で A_i := {x∈A | P(x, i)} のように，空集合にならない程度に絞り込むと，選択関数の構成は非常に難しくなります．そういう非構成的な要素，選択公理でしか存在を示すことができないような要素でも集めたものが A^ω です．

今回は，前回の「AI (Artificial Intelligence) とは何だろうか？トライアル」の逆に見えることを話すと最初に言いましたが，実は前回と同じことを言っているのだろうなと思います．つまり，

人間の内部的に機械を超えたものがあろうがあるまいが，伝達手段が A^* である限り，人間の能力と機械の能力は変わらない

という主張です．前回の話を「伝達手段」という観点から見直したということです．最後まで話してみると，話のとっかかりだったはずの「『好き嫌い』を論理式で判断していない」は本当に関係なかったですね．

目次へ

「モノ」を分けたがる人，境界が曖昧だと騒ぎ立てる人
- 悪党，愚者，正直者 -

2019 年 12月 28 日 (土)

以前のメモ「仕様は実装より分かりやすいか？（2019 年 11 月 16 日 (木)）」で，「仕様と実装はそれほど明確に区別できる概念では無いのではないだろうか？」と言いました．さらに言えば，私は，

それがなんであれ，書いた人が仕様と思えば仕様

なのだと思っています．動かない仕様を実装というのは無理がありそうですが，実装の方は一応作るべきものの機能を十分決めている訳です．どう作るのかと言ったところまで決めすぎているという欠点はありますが，決めていることに違いはないのですから，これが仕様だと言い張る人もいるかもしれません．もっとも，普通，「仕様」とは

作るべきシステムに要求されていることのみを記述
動く必要は無い
プログラムの作り方など利用者にどうでも良いことは書かない
結果として，記述がかなり簡潔になり，分かりやすくなる
できたシステムの正しさを判断するための基準になる

などのイメージがあり，それらの特徴に強力に合致しているものを「仕様」と呼んでいるんだと思います（たぶん）．

こういう，「仕様」と「実装」など，ちょっと見では「明らかに」違うと思われる対の概念やモノでも，境界が曖昧なものは色々あります．例えば，次のようなものです．

1	仕様	←→	実装
2	発明（特許における）	←→	既存技術の組み合わせ
3	システムをなす要素の集まり	←→	単なる要素の集まり
4	論文	←→	開発の報告書
5	アルゴリズム	←→	プログラムコード
6	AI のプログラム	←→	アルゴリズミックなプログラム
7	R の発音（英語の）	←→	L の発音（英語の）
8	意味（semantics）	←→	形式（syntax）
9	良いコメント（意味や意図を書く）	←→	悪いコメント（プログラムの直訳）

L と R は普段は英米人は明らかに違う音というのですが，フォルマントの特徴などから，人工的にこれらの中間付近の音を作り出すと，かなり判定が難しくなるそうです．

上にあげた例の中の「発明」とは特許法では

発明とは自然法則を利用した技術的思想の創作のうち高度のものをいう

となっています．「技術的思想の創作」という得体の知れないものも出てきますが，そのようなものの中で「高度のもの」を言う，というきわめて基準が不明瞭な定義になっています．技術の進んだ現在は，ほとんどの技術は既存技術の組み合わせですから，どんな組み合わせなら「発明」と言えるかが興味の対象になります．色々な基準がありますが，一つの基準は，その組み合わせ方による新しい効果があることです．これは上の表の，特許の下の行のシステムのシナジーにも似たところがあります．

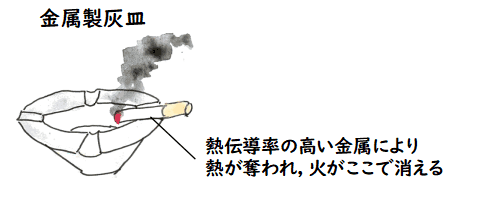
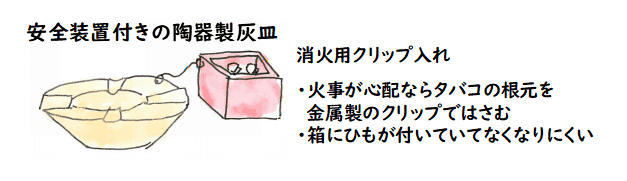
この新しい効果としては，次の「金属製灰皿」の例がよく持ち出されます．

金属製灰皿の発明
従来例として陶器製の灰皿があり，金属製の灰皿を作った場合，それを発明として主張できるか？
これは金属製の灰皿が従来なかったなら発明になる可能性が高い．一般に陶器の製品は落とすと割れやすいという性質があり，それを金属で作って，割れにくくするというアイデアは，他にも金属製の鍋などたくさん事例がある．しかし，この金属製灰皿はそういう壊れにくいという効果だけでなく，
金属製灰皿は熱伝導率が非常に高く，タバコの吸い口まで火が来る前に，灰皿のふちの部分で火が消えてしまい，火事になりにくい

という効果があり，これは従来にない新しい効果である．

これをはじめて聞くと，「ほー，なるほど．それは確かにそうだな」と感心するのですが，よくよく考えてみると

金属の熱伝導率が高いことは既知であり，それを利用したものもある．例えば，線香などを金属製のクリップではさめば，そこで消えるというのは既存技術だろう
金属製灰皿は，それを単に灰皿に組み合わせただけではないのか
既存の火を消す装置を灰皿につけても，それは既存技術の組み合わせであり，発明とは言えないだろうから，この金属製灰皿も発明とは言えないのでは？
他に作り方が簡単になるとか，消火装置を取り付けるのと違って出っ張りがないとかいろいろ特徴はあるのだろうけど，どこまで特徴が出れば発明というかは結局基準がないままじゃないか

という疑問が起こってきます．

私は昔，ある知り合いに対して「特許とは何だと思いますか？」と聞いたところ，多くの人は「新規性」とか「進歩性」とか答えるのに，彼は

「『驚き！』だと思う．」

と答えました．それを聞いて

「へー，この人はスゴイな．ちゃんと，人間の感性という観点から特許を認識しているのか．僕も，うすうすそうじゃないかと思ってたけど，こんなに完璧に言い切ることはできないもんな．」

と思ったことを今でも覚えています．特許の分野では，「発明の構成に人間を入れてはいけない」という不文律（有文律かも）があり，説明のなかから，極力，「人間性」を排除しようとするように思うのです．たぶん，これのおかげで，特許を生業としているような専門家と話すと，なかなか，発明の定義として実質的に「人間の感性」が入っていることを認めた会話にはならないのです．例えば，何か便利なことを思いついたので特許にならないかと専門家に相談すると

K さん，あなたのアイデアは単なる A 技術と B 技術の組み合わせじゃないですか．「進歩性」^*がありません．従来にない新しい技術は何かということを書いてくださいよ．でないと特許にはなりませんよ．

*「進歩性」：先行技術を元にその技術分野の専門家が容易に成し遂げることができないくらい難しいこと

といった答えが返ってくるかもしれません．そこで，生真面目に

いやいや，T さん．A 技術と B 技術が組み合わされている訳ですから，必然的に何らかのシナジーは生じている訳ですよ．それを「進歩性」が無いというのは単にあなたの感性じゃないですか．どれだけ「進歩性」があれば良いというんですか．私はこれで十分だと思いますよ^補足．

と返すと，こちらの話題のやり取りに移ってしまい，本来の特許に関する相談ができなくなってしまいます．こんな状態でも，特許の弁理士さんに大金を積めばなんとか知恵を出して書いてくれるのかもしれませんが，私は，今，無職なのでとてもそんなお金は積めません．そもそも弁理士さんに依頼するお金さえありませんし．

ということで，世の中には，

本来，対になる概念の間にきれいに区別がつくと思っている人と
その境界は実はあやふやで，分離の基準は多分に人間の感性によることを主張する人

の二種類がいるように思うのです．

ただ，「きれいに区別がつく」と言う人の中には，本気でそう思っている人と，実はあやふやな部分はよく認識しているのだけど，生業がなりたたなくなるので，「きれいに区別がつく」という態度をとる人の二種類があるように思います．私は曖昧な境界につい目が行ってしまう人なので，ここらあたりの人種の見極めは生きていくうえでとても大事なのです．ということで，次の二軸で整理してみました．

気付き軸：境界の曖昧なことに気付いているかどうか
態度軸：正直者か，悪党か

この二軸を使うと，次の表のように人間を整理することができます．私は，これを使って人との摩擦があまり無い付き合い方を心がけています．

	概念間の曖昧性に気付いている	概念間の曖昧性を気付いていない
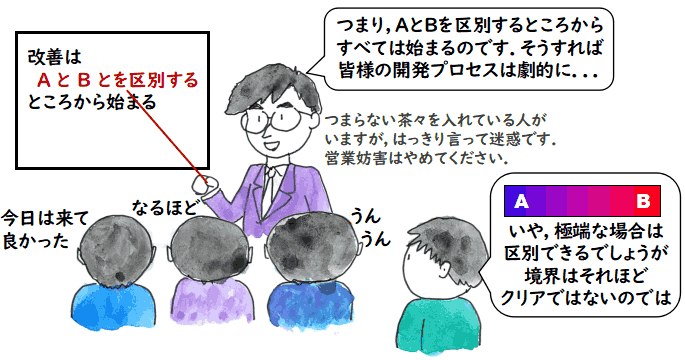
正直者	境界が曖昧性だと騒ぎ立てる	二つの概念の違いを一生懸命説明してくれる
悪党	明確な境界が引けないこともあると知りつつ，区別があると言う	＜この組み合わせはない？＞発明の基準が明確でないことに気が付いてない悪党は何をするのか？

私の知り合いには悪党が多いので，付き合いには細心の注意が必要です．正直者は，私と， KNDH さんと， KRM さんくらいで，残りはみんな悪党です．言葉の裏に隠されている「なにか」を常に読み取るようにせねばなりません．実は，正直者どうしの付き合いも大変です．まともにやると意見がぶつかり合います．つい先日，KNDH さんと３時間ほどお茶会をやって２日間ほど知恵熱を出してしまいました．

KNDH さんとのお茶会のイメージ図

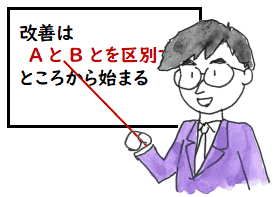
こういうふうに書いてみると，私は，すべての区別をなくしてしまいたい人のように見られるかもしれませんが，実は，区別をつけたがっている人なのです．

「仕様」と「実装」も，「発明」と「単なる従来技術の組み合わせ」も，「システムのシナジー」と「単なるコンポーネントの寄せ集め」も，これらが区別できる概念なら，いろいろな指針が立ちやすくなります．例えば，どうすれば「単なる従来技術の組み合わせ」が「発明」になり，私に大金を運んできてくれるかが分かる訳です．そうしようとするためには，やはり境界をよく考える必要があり，それらを明確に区別している人たちにお聞きする訳です．

もしかしたら，こういう，なかなか結論の出ない問題は，ある程度，役に立つところだけ使うというのが良い態度なのかもしれません．例えば，ここのメモで以前書いた「『物理学の応用について (寺田寅彦)』を読んで 2019 年 11月 23 日 (土)」では，寺田寅彦が

（物理学の）第一次の近似だけでもそのつもりで利用すれば非常に有益なものである．しかし学者が第一次の近似を求めて真理の曙光を認めた時に、世人はただちに枝葉の問題を並べ立てて抗議を申込む。

といった類のことを書いていると紹介しました．「仕様」も「実装」も我々の感覚で明確に区別できる場合が多くあります．そういうものを区別することは，ソフトウェアの品質を上げたり，工期を守ったりするのにとても有効っぽいです．世人たる私は枝葉の問題を並べ立てて抗議を申し込んでいるだけなのかもしれません．

でも，この第一次近似に満足していて，それが常に有効だと考えると進歩がないと思うのです．やはり，これらの概念をより有効に使うためには，境界の部分を明確にできるような概念の先鋭化，エッジを際立たせることが必要と思います．

したがって，本来は，第一次近似の利益を享受しながら，境界を磨き上げるという態度が必要なのだと思います．これはなかなか難しいですね．心の中に，相反する態度を保持することが得意な人と苦手な人がいるように思います．私は苦手な人です．

結局，今回のメモは，

相反するいくつかのテーゼを頭の中に抱えながら，利益を享受しつつ，より高次の理解に至る努力をする

という態度が良い態度なんだろうなというお話でした．「利益の享受」の最中にも次のステップに向かうヒントが出てくるかもしれませんものね．

（補足）「．．．私はこれで十分だと思いますよ．」で，ブレードランナーという映画（1982）の冒頭の部分の場面で，

主人公（ハリソン・フォード）：「四つくれ」
屋台の（日本人っぽい）おやじ：「二つで十分ですよ」
主人公（ハリソン・フォード）：「いや，四つだ」

を思い出してしまいました．あれを覚えている人は結構いるみたいですね．検索語

ブレードランナー十分ですよ

で検索をかけてみると，結構たくさん見つかります．

う～ん，主役はハリソン・フォードだったんですね．

ちょっと，絵がてきとうすぎたみたいです．．．

目次へ

AI (Artificial Intelligence) とは何だろうか？トライアル

2019 年 12月 25 日 (水)

前回予告したように長いので，目次を書きます．

ことの始まり

AI の定義（トライアル）

1. この主張の理由付けといくつかの例

2. ほかのいくつかの（仮想的な）主張に対する反論

2.1 「究極的な AI は機械と違う人間の計算論理で動くべき」に対する反論

2.2 「閉じたシステムは AI ではない．センサとアクチュエータを持つものが AI」に対する反論

3. AIは人間の知能を目指すべきか？

ことの始まり

私が時々行く勉強会で，「AI とは何か？普通のソフトウェアとどう違うのか？」ということが問題になることがあります．これは，

「あーでもない．こーでもない．それはちがう．．．．．」

と言った感じで大もめします．

おまけに，この問いは突然でて来て，議論している人たちは資料もなく，発話のみのやり取りで議論するので，各自の主張がなかなか掴みにくいものです．聞いていると同じ人の主張がだんだんずれてくるようにも思います．この問いの根っこには「人間と機械はどう違うのか？」という疑問をはらんでいるような気がします．つまり，議論している人たちは，

（人間の知能を目指している）AIと機械（の計算可能性）はどう違うのか？
= 人間と機械はどうちがうのか？

という問いが深層心理の中にあるのでしょう．もしかしたら，心の中には明確なイメージ，あるいは理想があるのかもしれませんが，表現として出してみると，その発話者自身「なんか違うな」と思って，言いなおし，それでだんだんずれてくるのかもしれません．あるいは，聞いている側もしっかり把握できていないので相手の主張が揺れているように思えるのかもしれません．

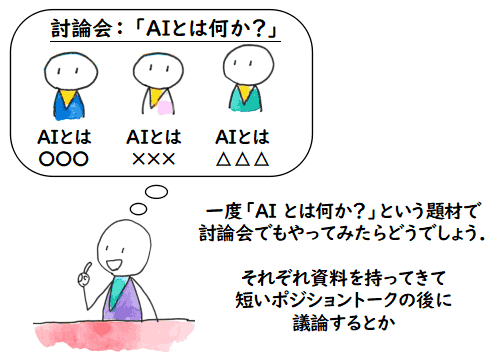
私はその勉強会で，一度「AI とは何か？」という討論会でもやってみたらどうだろうかと提案したことがあります．数人がそれぞれポジショントークをやって議論してみるわけです．どうせ発散して収束はしないでしょうが，それぞれ自分の立場の資料は持ってくるわけですから，それぞれの立場はより明確になりますし，資料作成と議論で自分自身を見直す良い機会になります．

そのときの提案は，思い付きであまり練れてなかったことと，私自身はポジショントークするとは言わなかったことからお流れになってしまいました．やはり自分が話す気になって提案しないと良くないなと思いましたので，その第一歩として，今回，思うことをちょっと書いてみようと思います．ここは，「メモのような日記のような」ですので，あまりしっかりしたものでなくとも，後々，ポジショントーク用の資料の核になれば良いかなというくらいの気持ちです．

ポジショントークをする前に，自分自身の AI に関する関わりを簡単に述べておきます．基本的には「ほとんど知らない」ですが，具体的にいうと以下の通りです．

1981年ごろ大学の４年生のゼミで古典的な AI を学びました． A* などの探索アルゴリズムや述語論理での自動証明の基礎などです．でも，主に学んだのはもう一つのゼミでのプログラムの意味論とか検証とかそれに必要なそのほかの計算機科学の基礎一般の方でした．だから，ここでは AI は片手間にやってみただけです．
会社では 1980 年代に AI ブームだったので，その応用的なテーマとして，エキスパートシステム構築ツール関係の仕事に関与していたこともあります．あまり深くはやりませんでしたが，ルールベースシステム，意味ネットワーク，フレーム理論，フレーム問題，仮説推論，定性推論などの言葉に関しては耳年増になっています．
ニューラルネットワーク，遺伝的アルゴリズムあたりまでは何とか分かりますが，その後はほとんど知りません．特に，最近はやりのディープラーニングなどはまったくと言っていいほど知りません．

このくらいの知識で思うことを書きます．

AI の定義（トライアル）

私の主張の本質は単純で，次の３つです．

AI (Artificial Intelligence) は，普通のソフトウェアと変わらない
（普通の）ソフトウェアの中である特徴群が顕著なソフトウェアを AI と呼ぶ
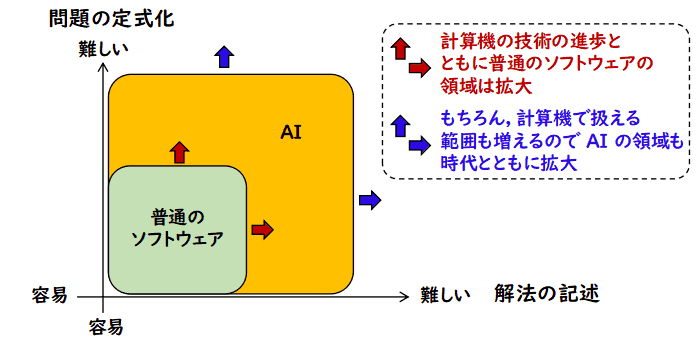
その特徴群とは「問題の定式化の難易度」と「解法の記述の難易度」であり，これら二つがともに小さいものが所謂「普通のソフトウェア」であり，どちらかが限界を超えて大きいものを「AI」と呼ぶ．
その特徴の度合いはテクノロジーの進歩とともに変わる
計算機の進歩とともに計算機で扱える問題の範囲は拡大するので，ソフトウェア全体は常に拡大している．ここでの AI の定義では，その中で問題の記述や解法の記述が比較的小さいものを「普通のソフトウェア」と呼んでいる．問題の記述の方法も解法の記述の方法も日々進歩しているので，「普通のソフトウェア」の領域は拡大していくが，全体も拡大していくので，「AI」の部分も拡大していく．

「AI」というなんだかわからないものを，「問題の定式化の難易度」と「解法の記述の難易度」という二つの軸で整理したわけです．これを２つの軸に分解されてよりコンパクトなとらえやすい問題になったと考えるか，あるいは，よけい訳の分からない２つの軸を導入したことで二倍わからなくなったと考えるかは，人によって違うと思いますが，私としては二つのより小さな問題に分解したつもりです．

主張だけでは何ですので，以下の項目について述べて，上の主張の理由付けと補強をしたいと思います．

この主張の理由付けといくつかの例
ほかのいくつかの（仮想的な）主張に対する反論
1. 究極的な AI は機械と違う人間の計算論理で動くべき
2. 閉じたシステムは AI ではない．センサとアクチュエータを持つものが AI
AIは人間の知能を目指すべきか？

では，それぞれについて意見を述べます．

1. この主張の理由付けといくつかの例

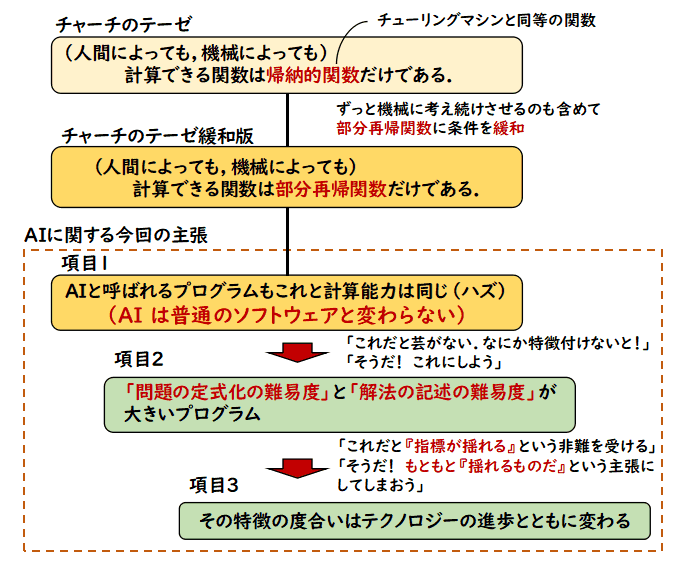
上では，私は３つの項目で AI を特徴づけていますが，本質的なことは１つ目です．つまり，

AI は普通のソフトウェアと変わらない

という主張が核となっています．これはチャーチのテーゼ

チャーチのテーゼ
計算できる関数は帰納的関数だけである

に基づきます．つまり，計算できる関数はチューリングマシンやラムダ計算で計算できる関数だけということで，もっと言えば，コンピュータの普通のソフトウェアで計算できるものだけという提唱です．帰納的関数は「どんな入力に対しても必ず停止すること」という条件が付けられますが，ここではずっと答えを求めて走らせ続けてもよいので，帰納的関数を部分再帰関数（帰納的関数と同じ作り方なのですが，ある入力に対しては停止しなくなるかもしれない関数のこと）に変えておきます．並列計算を考えれば一つのプロセスを走らせ続けておいても，次の問いには対応できるので，人間の能力を模したものという意味ではこう考えておいてもよいでしょう．

私自身はチャーチの提唱を信じているというか，信仰しているので，「AI は普通のソフトウェアと変わらない」という答え以外に無いのです．でも，これだと，聞いてる人からは不満がでるでしょうから，なんとか定義している体裁を保つために，ウーンと頭をひねって，

問題の定式化が難しい
and/or
解法の記述が難しい

という特徴を上げました．これはもちろん適当に上げたわけではありません．過去の AI と言われるソフトウェアを見てきて共通の特徴を上げてみたのです．

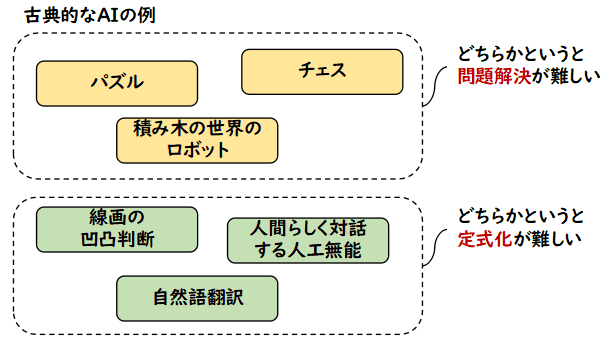
初期の AI をいくつか挙げてみます．

パズル（15パズル，ルービックキューブなど）を効率よく解くことができるもの
積み木の世界で指定された動作を行うための高度なプラニングを行うロボット
チェス，囲碁，将棋など，ゲームで強いプレイヤーとして演じるもの
線画から立体を認識するもの
人間と対話し，それが人間だと思わせるような会話を行うもの（doctor, eliza 等の所謂，人工無能）
一つの言語から別の言語へ翻訳するもの（自然語翻訳）

前の方のパズル，積み木の世界のロボットのプラニング，チェスなどのゲームは，問題自身は明確なのだけど解き方が分からないソフトウェアです．そのため，決まった手順で問題を解くのではなく，探索を使って問題を解く手法がたくさん開発されました．しかし，15 パズルやルービックキューブなどのパズルは最初はなかなか解き方が分からないのですが，次第に，群論とか半群論とかを用いて解析されて行って，いくつかの基本的な定理の組み合わせで解けるようになってきます．そうすると，それらを解くプログラムも探索を大規模に使うものではなく，比較的手続き的になってきます．例えば，いくつかの条件判定や小規模な探索で初期の素解を求めて，それを最適化するなどの解き方になってくる訳です．そういうものは段々 AI とは呼ばれなくなってきます．今日，ハノイの塔のプログラムなどは誰も AI とは呼ばないでしょう．でも，はじめてあれを解けと言われた人間にとっては結構難しいものなのです．

後半の線画からの立体の認識や人工無能，自然語翻訳は問題の定式化自身が難しい例です．線画からの立体の認識は問題を限定すれば定式化はある程度できます．例えば，

点の間が直線で結ばれている図形から，線のつながり方の制約から，各線が飛び出しているのか，引っ込んでいるのか，あるいは物理的に無理な接続の仕方なのかを判定せよ

という問題なら，定式化は線のつながり方の制約を列挙する位でしょうが，「人間がどのように凹凸を判断しているか？」というところから考えると問題はそれほど明らかではないでしょう．

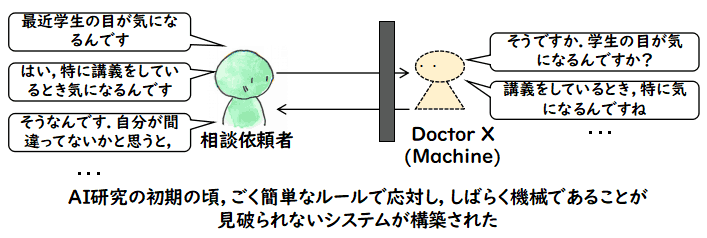
人工無能の例は

どういう対応だったら，人間はその対応をしているものが人間であると感じるのか？

という問いへのアプローチなのだと思うのですが，この問いはなかなか定式化することができません．

そのために，いくつかの仮説を立てたり，実験的に対話させてみて，不自然に感じるところを修正していくことになると思います．

自然語翻訳も簡単なものなら，二つの言語の間の文法の対応規則の適用ということになるでしょうが，そうやってできた翻訳文には我々はすごい違和感を感じます．そうすると，「自然な翻訳とは」と言った定式化の難しい問題が出てくる訳です．

これら「人間の感じ方」に依存していて，定式化の難しい問題も，「人間の感じ方」の部分に関する知見が蓄積されてくると，定式化可能な部分が多くなってきます．線画からの凹凸の判断などは典型的でしょう．この問題に初めて出会った時は，人間がどう判断しているか分からないのですが， 1960 年代の初期の段階ですでにいくつかの凹凸判断のルールが抽出されていました．自然な会話の条件やこなれた自然語翻訳の断片的なルールもいくつか発見されていて，長時間，機械だと判断できない会話ソフトウェアや極めて自然な翻訳文を生成するソフトウェアなどが出てきています．

先走りましたが，こういう，

人間が自然と感じる基準の蓄積によって定式化が可能になることや
最初は解き方が分からず，探索だけに頼っていたものが，次第に手続き化して効率の良い問題解決になっていく

というAIの特徴から３つ目の項目

その特徴の度合い（問題の定式化と解決方法の記述の難しさの基準）はテクノロジーの進歩とともに変わる

を上げています．

以上，古い時代の AI の知識から，AI とは何かを論じましたが，現在のディープラーニングなどのテクノロジーが入ってきても，「問題の定式化と解決方法の記述の難しさを　AI の基準にとる」ことはまだ有効なのではないでしょうか．インターネット上の膨大な画像からネコを判定するプログラムも問題の定式化と解決方法の両方が難しく，ディープラーニングはこのような問題に対応できるという解釈でいけるかなと思います．

また，最初はディープラーニングなどで無理やり解いたとしても，そのうちにディープラーニングで学習した結果のデータからいくつかの概念整理の技術などが出来てくるかもしれません．そうすると，人間とのうまい対話を学んだ AI システムから「人間とのうまい対話」に必要な条件を記述するための諸概念が整理されるでしょう．人工無能も，問題の定式化と解法の記述，ともに不明な部分が少なくなっていく訳です．

以上，私が思う AI の特徴づけの基本的な考え方を述べました．次は，ほかの人たちが提案している AI の特徴づけに対する反論と最後に AI は人間を目指すべきかに関する意見を述べます．

2. ほかのいくつかの（仮想的な）主張に対する反論

ここでは「AI とは何か」に対する二つの仮想的な主張を相手取って反論してみます．あくまで「仮想的な」主張で，実際の誰かの主張という訳ではありませんので反論は一方的です．こういう「妄想」に対する議論は，般若心経の

菩提薩埵依般若波羅蜜多故
心無罜礙無罜礙故無有恐怖遠離一切顛倒夢想
究竟涅槃

に反する行いで，心の平安からは遠いところにあるのですが，主張の差を認識する上では有効な手法と思います．

考察する主張は次の２つです．

究極的な AI は機械と違う人間の計算論理で動くべき
閉じたシステムは AI ではない．センサとアクチュエータを持つものが AI

2.1 「究極的な AI は機械と違う人間の計算論理で動くべき」に対する反論

上では，チャーチのテーゼに対する信仰で，「AI は普通のソフトウェアと変わらない」という主張をしました． AI について述べる人の中には，「人間は機械ではできないことができる」と信じている人たちもいます．したがって，そこを目指す AI も究極的には機械と違う原理で動くべきだという考えがでてくると思います．「機械と違う原理で動く機械を目指す」というのはなんか変な気がしますが，ここでは「人間は機械にできないことができるのか？」についてちょっとだけ考えてみます．

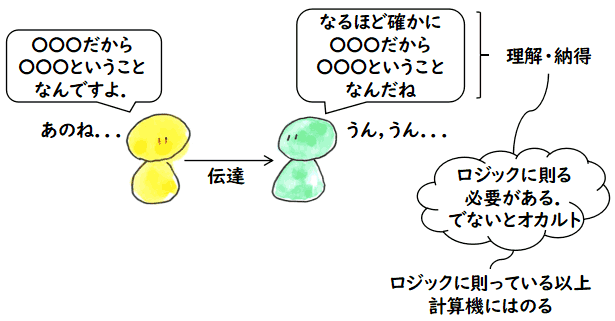
私は，「人間のできることは機械でもできる」という立場をとります．もう少し正確に表現するなら

人間の思考で結論して，他人に説明できることは，機械でもその思考の過程をシミュレートできる

です．例えば，誰かが，何らかのスゴイ推論をしてある結論を出したとします．

それを他人に説明するときは，聞いている人の理解を得るためには，推論がきちんとした論理でつながっていなければなりません．そうでないなら，

「説明はできないけれど，俺はスゴイ結論を得た．信じられないかもしれないがこれは本当のことなんだ」

ということで，オカルトの類です．もし，その人の話が論理的に正しくつながっていれば，それは機械でシミュレートできるはずです．したがって，あることが他人に説明して納得してもらえるものである限り，それは機械にも出来ることなのです．逆に言えば，機械にできないことは人間が他人に伝えて納得させられないことです．ということで，「計算機にできないが正しいこと」の例をあげた瞬間にそれは計算機でできることになってしまいます．つまり，そんな例は示すことができないということです．

よく，「ゲーデルの不完全性定理」を出して，人間と機械の能力の差を言う人がいます．これはもともとゲーデルの不完全性定理の周辺が，ある程度混乱しやすい状況があるのかなと思います．というのも，ゲーデルの不完全性定理の解説に

正しいけれど，証明できない命題が存在する

という文言が頻繁に出てくるからです．これから，ある人たちは

人間には正しいということが分かるけれど，機械にはそれが出来ない命題が存在する．言い換えれば，人間は機械が真であると知ることができない真なる命題を知る能力がある．

と考えて，人間と機械に差を置き，心の安定を図るのだと思います．また，別の人たちは，人間と機械の差ではなく，神のようなものと人間の差ととらえて，「真なる命題だが，人間にはそれを知ることができない命題があり，それが人としての知性の限界を示している」と考える人もいるみたいです．とにかく，ここでは「正しいけれど，証明できない命題」の「正しい」の意味を正確に把握することが重要だと思います．

これらについて簡単に述べておきます．

ゲーデルの（第一）不完全性定理は，

ある程度強く，かつ，系統的に列挙できる公理系では，必ず証明も反証もできない命題が存在する

ということを言っています．この時点ではそれほど問題の無い文言だと思いますが，その証明も反証もできない命題の例が上で述べた，所謂，

正しいけれど証明出来ない式

なのです．これを解説します．

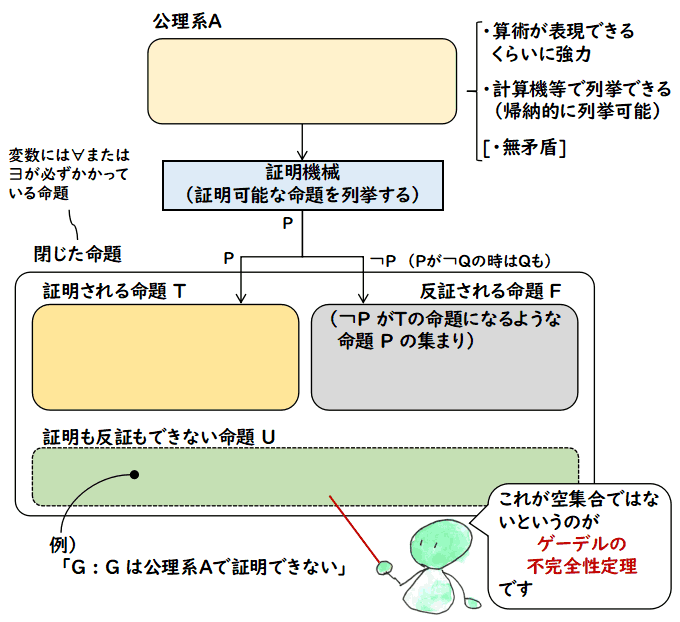
次の図はゲーデルの（第一）不完全性定理の内容

算術が表現できるくらい強い公理系で，かつ，その公理が計算機などで列挙可能で，かつ，その公理系が無矛盾なら，証明も反証もできない閉じた命題がある

を表しています（正確には，ゲーデルの後，少し補強されたものですが）．「閉じた命題」というのは，その命題に現れるすべての変数に全称記号 ∀ か存在記号 ∃ がかかっていて，変数の値で真偽が変わらない命題のことです．ここで「命題」と言っているのは，正確には数理論理学でいう「論理式」のつもりです．全称記号 ∀ や存在記号 ∃ が現れる式です．あまり論理学を知らない人には「論理式」という言葉は分かりにくいだろうと思い，より一般の言葉である「命題」を使いました．逆に論理学を知っている人には，命題論理の「命題」と勘違いさせるかもしれないので一応断っておきます．また，上で公理系の条件に「無矛盾である」を入れましたが，矛盾のある公理系では，すべての命題が証明されてしまい，通常，それは我々が望む状況とは異なりますから，以後，「無矛盾性」の条件ははデフォルトでついていると思ってください．

図を説明します．何か公理系Aを定めたとして，その公理系は算術が表現できるくらい強力で，公理を計算機等で列挙することができるものとします．そうすると公理から推論規則（普通は三段論法（modus ponens）と全称化（現れる変数に全称記号 ∀ をつける推論規則））を使って証明可能な命題を次々に生成していく証明機械を考えることができます．この証明機械が生成していく命題を P とします．それを「証明される命題 T」に溜めていきます．また，同時に P の否定￢P は「反証される命題 F」の方に溜めていきます．これは反対の証明が見つかる命題で絶対に偽の命題です．P が￢Q の形のときは，Q もこの F に入れておいて良いでしょう．

先ほど言いました閉じた命題，つまりその命題に現れる変数すべてに ∀ か ∃ が掛かっていて，変数への割り当てに関わりなく真偽が決定している命題について，上の機械証明の手続きはそれを「証明される命題 T」か「反証される命題 F」のどちらかに必ず分類できるだろうかという疑問が生じます．

ゲーデルの（第一）不完全性定理は，そうではなく，第３の分類の「証明も反証もできない命題」があるということを言っています．これが十分強力な公理体系に対して機械的な証明ができない理由になっています．このことについては後で詳しく述べます．

このような「証明も反証もできない命題」の例としては，自己参照を使った命題

G : G は公理系A で証明できない

と言ったものがあります．公理系Aに条件

算術が表現できるくらいに強力
計算機等で列挙できる（帰納的に列挙可能）

をつけているのは，G のような命題を作れるようにするためです．つまり，

「算術が表現できる」はその体系の中のデータで，G のような論理式を符号化できるようにするためです．代わりに文字列が扱えるといっても構いません．ゲーデルの不完全性定理はコンピュータができる前に出されたので，ゲーデル数のような難しいもので論理式を符号化していますが，今だと， ASCII 文字列で論理式を符号化すると思えばよいでしょう．あれも，ビット列なので，長い ASCII 文字列は，実はとてつもなく大きな数なのです．
正確には命題の字面だけでなく，その字面の意味も記述できる必要があります．例えば，"(1 + 1 + 1) mod 2 = 1" を符号化した結果を受け取って，"true" を符号化したものを返す関数がその公理系で定義できるなどです．算術でもある種の簡単な文字列の体系でもそれはできます．
もう一つの，「公理が計算機などで列挙できる」は，G の中で述語として用いられる「証明できる」を記述可能にするためです．公理が，ある帰納的関数 ax(n) を使って，ax(0), ax(1), ax(2), ... と列挙できるなら（次の図を参照）
AX(n) := {ax(i) | i ≤ n}
TH(n, m) := 公理の集合 AX(n) を使って，長さ m の証明で証明できる命題
とおけば，命題 P が証明可能であるということは
ある n と m があって，P が命題の集合 TH(n, m) に入っている
になります．これは，k = 0, 1, 2, ... に対して， n + m ≤ k の組 (n, m) の TH(n, m) を調べていけば機械的に調べることができます．集合論で有理数が可算集合であることを証明するときの方法と同じですね．

ということで，公理系 A が算術を表現できるだけ強力で，計算機などで列挙可能なら，

G : G は公理系A で証明できない

という命題を作ることができるようになり，この G が仮に証明されると，その内容は G は証明できないですから，矛盾となり，また，これが仮に反証されると，G に内容の否定，すなわち，G が証明されるとなって，これも矛盾が生じます．まとめると，

G が証明される => G は証明されない => 矛盾
G が反証される（￢G が証明される）=> G が証明される => 矛盾

したがって，G は証明も反証もされないので，証明できないことがわかり，次の図（先ほどの図の再掲）で「証明も反証もできない命題 U」が空集合ではなくなる訳です．

もし，仮に U が空集合なら，機械で次々に公理から証明を作り，「証明される命題Ｔ」と「反証される命題Ｆ」を作っていくことで，どんな閉じた命題の真偽も決めることができます．つまり，C 言語風に書くと

  /* P は証明されるか反証されるかを調べるために与えられた命題 */
  k = 0;
  while (FOREVER) {
    for (n = 0; n < k; n++) {
        if (P が TH(n, k-n) に入っている) {
            return P は証明される;
        } else if (not P が　TH(n, k-n) に入っている) {
            return P は反証される;
        }
    }
  }

のような手続きで，証明可能か反証可能かを調べることができる訳です．しかし公理系が十分強くて，かつ，計算機などで列挙できる場合は，U が空集合にならないので，真偽を決められない命題がでてくる訳です．上の C 言語風の手続きでいうと，入力の命題 P として，先ほど作った命題 G，つまり，

G : G は公理系A で証明できない

が与えられると，上のC 言語風の手続きは停止しません．つまり，「証明も反証もできない命題」の存在が機械証明を不可能にしている訳です．

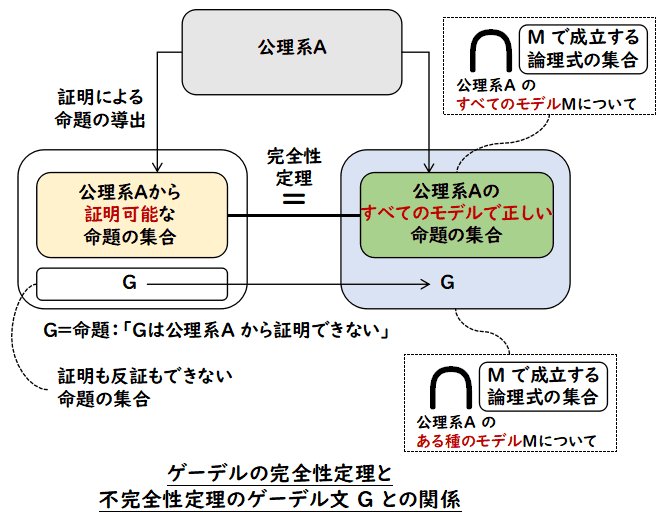
もう一つの前提知識として同じくゲーデルによる完全性定理を述べておきます．完全性定理は

公理系A から証明できる命題の集合は公理系Aを満たすすべてのモデルで成り立つ命題の集合の共通部分と等しい

です．ここでモデルとは，命題を構成するモノの記号，関数記号，述語記号になにかある世界（集合）の要素，その世界での実際の関数，述語を当てはめてみて，与えられた公理系 A の中の公理が成立するもののことを言います．もう少し詳しいことをレーベンハイムスコーレムの定理の解説のところに書きました．話をもとに戻して，完全性定理の名称の「完全性」この命題の右から左の方を指していて

公理系A のモデルすべてで成り立つ命題は，公理系 A で証明できる

つまり，ゲーデルが想定している証明システムは，真なる命題を完全に証明できるシステムであるという意図です．

（第一）不完全性定理の「完全」という意味と完全性定理の「完全」という意味は違う意味で用いられています．

第一不完全性定理での「完全」
すべての閉じた命題 P に対して，必ず，P か￢P のどちらか一方が証明される
完全性定理での「完全」
すべてのモデルで正しい命題は，その証明システムで証明することができる

まず，この二つの異なる「完全」という用語が誤解に拍車をかけていますので，ここは正しく認識しておく必要があります．

これで議論するための前提の知識を説明し終わりましたので，いよいよ核心の命題 G の話に入ります．

我々の関心の的の命題 G をもう一度書いておきます．

G : G は公理系A で証明できない

G は（第一）不完全性定理により，確かに公理系A からは証明することができません． G の内容は，「G は証明できない」ということで，しかも，確かに証明できないのですから，ちょっと考えると

G は正しいけれど証明できない命題

ということになります．

ここで「正しい」の意味が問題になります．通常の，数理論理学での意味である「公理系A のすべてのモデルで成立する」という解釈をすると，明らかに完全性定理と矛盾してしまいます．完全性定理は，

その命題が「公理系A のすべてのモデルで成立する」ならば，その命題は「公理系A で証明できる」

と言っていますので，「G は証明できる」ことになってしまいます．したがって，「正しい」は別の意味です．

「G が正しい」ことを導いたのは誰で，それはどこで行われた推論だったかを思い起こす必要があります．

「G が正しい」ことを導いたのは，我々であって，それは公理系A や証明システム，モデルをメタな立場からみたメタな推論においてであった

のです．ここで，「メタな立場」とは，公理系A や証明システム，モデルに関する我々の議論の立場であす．また，それと対の用語として，公理系A や証明システム，モデルの中で行われる推論や正しさの評価を「対象世界の立場」と言うことにします．対象世界の立場としては，G は次の図のような扱いになります．つまり，完全性定理から，証明される命題の集合は，すべてのモデル M で成立する命題の共通集合と一致します．G は証明も反証もできない命題ですから，右側の「すべてのモデル M で成立する命題の共通集合」には入っていません．もちろん，反証もできない命題ですから，G が成立するモデルは存在します．むしろ，多くの我々が普通と思うモデルで成立するみたいです．しかし，すべてのモデルを考えたとき，G の成立しないモデルが現れてきます．

G はこういう立場の命題なのです．

では，先ほど行った

G は正しいけれど証明できない命題

を導いた推論はどこにいったのでしょうか．これはメタな立場の推論なので，我々の推論のシステムを何らかの公理系で規定したとき成り立つ推論です．このとき用いた推論は，高々，背理法程度なので，この推論もメタなレベルの適切な公理化と推論ルールの設定で，機械でシミュレートできるはずです．

ということで，ゲーデルの不完全性定理は，別に人間ができることと機械ができることの間に境界を設けたものとは考える必要はないという説明を終わります．混乱の原因は，

「完全性（completeness）」という単語が，完全性定理と不完全性定理で別の意味で使われていること
- 完全性定理の中では，「モデルの意味で正しい命題がすべて証明可能である」という意味で使われ
- 不完全性定理の中では，「任意の閉じた命題 P について P か￢P がのどちらかが必ず証明される」という意味で使われている
証明も反証もできない命題の例 G が
正しいけれど証明できない命題
と言われること

によります．

人間と機械の能力に差がある根拠とみなされがちだった不完全性定理に関する状況を一応整理したところで，最初の議論に戻ります．

今まで述べたように，私は AI が目指している人間というものが機械より優れた推論能力を持っているとは考えておらず，人間と機械は同じ推論能力であると考えています．また，その推論能力は計算の言葉に言い直すと，帰納的関数（あるいは，部分再帰関数）です．

しかし，最近，量子計算など，従来と異なる計算モデルが出されてきています．したがって，将来，帰納的関数より強力な計算原理が発見される可能性は否定はできません．でも，そうならそれを計算機に組み込むことによって，現在，「帰納的関数」と言っている計算能力のベースをその見つかった「（新）帰納的関数」に置き換えれば，「人間のできることは機械にもできる」ということに変わりはないと思います．もとの主張が動いている気がして，ちょっと卑怯な気がしますが少し逃げを打っておきます．

もう一つ逃げを打っておきます．ここでの議論は一階述語論理のお話で，二階以上の高階論理の場合は，私はあまり良く知りません．でも，なんとなくですが，大丈夫じゃないかと思います．人間が推論したことを他人に納得してもらうには，論理が必要で，どこかの階では，こういう一階の論理学を使った説得が入る訳ですから，その部分で機械でシミュレートできるはずです．

2.2 「閉じたシステムは AI ではない．センサとアクチュエータを持つものが AI」に対する反論

もうひとつ，私の知り合いに，

AI の特徴はセンサとアクチュエータを持つことであって，センサを通して外界から得られる膨大な刺激に対して，アクチュエータでアクションを起こし，そのフィードバックで学習を行うシステム

と言われる方がいます．私自身，センサとアクチュエータの重要性は否定しませんし，実際，人間はそれによって進化の中で，現在の能力を獲得したのだと思います．

しかし，センサとアクチュエータの有り無しをもって，AI かそうでないかを定義するのは違うんじゃないかなと思いますので，ここで少し反論しておきます．もっとも，私はその方の主張を全部聞いたわけでなく，上の文言を聞いたくらいの状態ですので，これも仮想的な主張（私の妄想）に対する反論な訳です．どちらかというと，今度議論するときのための下準備です．

上の定義への不満は２つあります．

AI が必ずセンサとアクチュエータを備えることとなると，これに合致しない現在の多くの AI システムが出てきてしまう．私らがお手上げな複雑な探索やプラニングを行ってくれるシステムなどは AI と呼びたい
センサとアクチュエータだけを取り上げて，計算部分に関する特徴づけが無いと，結局，ソフトウェアとしては普通のソフトウェアと変わらないことになってしまう

一つ目は，現状 AI と呼んでいるものの多くが AI と呼べなくなって不便だということ位なので実は大したことではありません．「呼び名を変えれば良いのかな」位の話です．重要なのは２つ目です．これも，計算能力としては普通の帰納的関数で表現されるものということなら，別に問題はないのですが，それを超えるきっかけとなる因子と考えるならそれは違うのではないかと思う次第です．

確かに，センサーとアクチュエータを持ったシステムを絵に描いてみると，なにかすごいことができそうな気がします．センサーを通して得た膨大なデータから判断したアクチュエータを介した外界への働きかけ，そしてそのフィードバックの獲得，そのサイクルの中でも推論部の学習，このようなプロセスで従来のソフトウェアでは実現しえなかったような学習が行われ，「知能」というものに近づいていくような気がします．

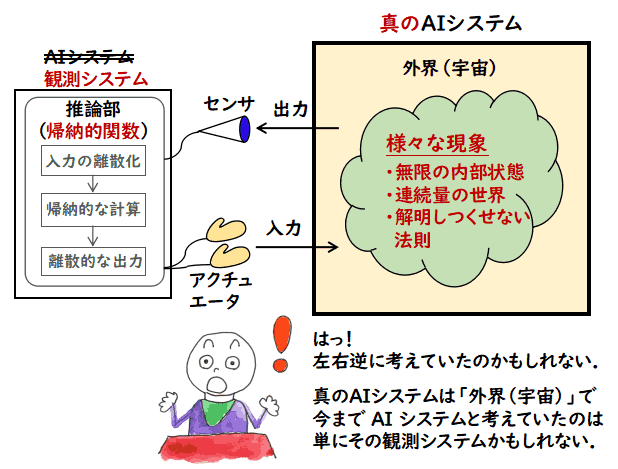
でも，疑問もあります．推論部が帰納的関数のままでは，結局，次の図のように， AI システムは取り込んだデータを離散化し，普通の帰納的関数で計算し，それをアクチュエータに出力するだけなので，やれることは普通のソフトウェアと同じなのではないでしょうか．これは推論部にどんな技術を使ったとしても，いまだに，帰納的関数以上の計算能力を持った計算原理は発見されていないのですから，このようにセンサとアクチュエータを備えたとしても，しょせんは普通のソフトウェアと原理的には変わらないということになりそうです．「フォン・ノイマン・ボトルネック」の言葉を真似すれば，「推論部ボトルネック」あるいは「計算原理ボトルネック」です．

もちろん，「AI は，普通のソフトウェアと原理的には変わらないが，その中でセンサとアクチュエータを備えたものを AI と呼ぶ」という，普通のソフトウェア内の分類という立場なら，別に構いませんが，そうでなく別の原理を見つけたいというのならやはり，帰納的関数の部分からいじらないといけないように思います．

もしかして，上の図のように，「入力→計算→出力」というような構成でしかシステムを考えることができない私の頭が固いのでしょうか？

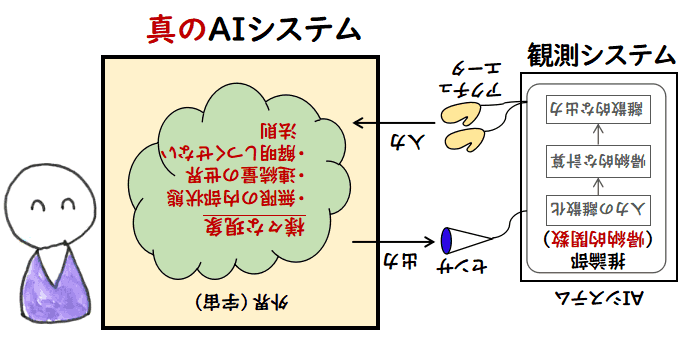
はっ？　もしかしたら図の見方が逆なのかもしれません．真の AI システムは図の右側の外界（宇宙）と書いた方で，今まで AI システムと思っていたのは，その観測システムなのかもしれません．

確かに，宇宙でしたら，有限だか無限だか分からない状態を持ち，連続量を伴う現象が起き，そして解明しつくせない法則が支配していて，帰納的関数の束縛から自由であるのかもしれません．右側の AI システムのふりをした観測システムは，アクチュエータを介して，真の AI システムに入力を行い，宇宙空間でなされた不可思議な計算結果を，センサで受け取っているのかもしれません．

しかし，これだと，帰納的関数を超えたものを「宇宙」というなんだか分からないものに押し付けただけなので，何らかの新しい原理を提案することが必要になってくるのではないでしょうか．

ということで，私にはまだ，センサとアクチュエータを備えた AI の提案が，単にソフトウェアの分類を与えているのか，新しい計算原理を提案しようとしているのか分かっていません．

今度，ぜひ，その方の主張の深いところまでをお聞きしたいのですが，そうすると，必然的に私自身もその議論に深くかかわることになり，それほどの能力の無い私は辛い目に合わなければならなくなるのです．その決心がついたら．．．あるいは，誰か援護射撃をしてくれる人がいる状況を狙って．．．

3. AIは人間の知能を目指すべきか？

これまでさんざん，AI は人間を目指していると文中では書いたのですが，今回私がやった特徴づけは，

AI とは，仕様が作り辛いソフトウェア and/or 解法が作り辛いソフトウェア

ということで，人間を目指しているという項目はありませんでした．もし，その条件を入れると，やはり「人間て何？」という問いに答えないといけません．私はこれに答えられないし，答えようとすれば機械と変わらないという答えにならざるを得ないので，この条件は入れられないのです．

ということで，私としては，AI は人間を目指すという立場ではなく， AI は単に難しい問題を解いてくれる便利なソフトウェアという立場を取ることにします．そして，人間を模すのは，そのような高度なことをやってくれるシステムのお手本として人間があるからに過ぎないという立場を取ります．その高度なことをやるためのヒントの候補であって，もし，ほかの方法で解けるなら，人間のやり方を想像しながら真似る必要はないと思うのです．

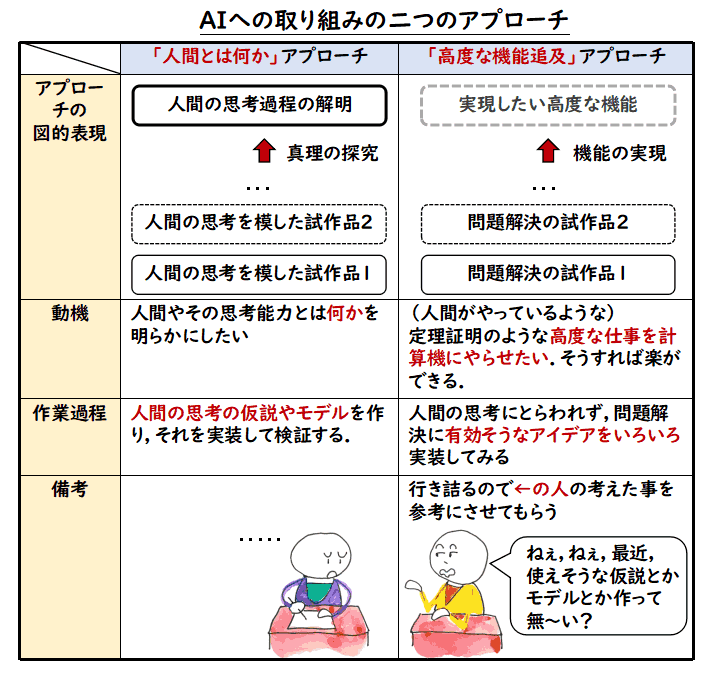
世の中の AI 研究のアプローチに大きく２種類あるのかなと思います．

「人間とは何か」アプローチ
人間とは何か？人間の思考能力とは何かを知りたい人たちのアプローチ
「高度な機能追及」アプローチ
人間がやっているらしい高度な仕事をやれる機械を作りたい人たちのアプローチ

私自身は「高度な機能追及」アプローチです．もっとも，いま，AI をやってないので，「やるとしたら」のお話ですが．

これを図にしてみました．

「人間とは何か」アプローチでは，人間の思考過程の解明などが最終目標になっていて，そのモデルなどを作り，それを検証するために何か試作品を作ってみて，モデルを修正していきます．一方，「高度な機能追及」アプローチは，なにかスゴイ機能を作りたいのが動機ですから，人間がやっていることにこだわらず，役に立ちそうな方法は試してみます．機能実現のために無節操にやっててもすぐアイデアが枯渇して行き詰ってしまうので，ときどき，「人間とは何か」アプローチの人たちがどんな仮説やモデルを作っているのか覗いてみるとブレイクスルーになることがあります．

私としては，「人間とは何か」という問いに真剣に取り組む人は絶対必要だと思います．このような人たちは，常に，一定量いていただいて，一生懸命に考え続けていただきたいのですが，

自分がそれになろうとか
そういった人たちとの議論に巻き込まれる

のはちょっと性格上合わないかなといった気持ちです．あくまで，必要になったときに利用できる部分を参照させていただければありがたいのです．世の中の役割分担，各自が得意な分野で頑張るということで，まあ，良いのではないかと思います．

以上，今回のメモは，たぶん，「今後の AI の発展に向けて」の考察だと思います．

今日のお昼に KNDH さんとお茶をしながら思い浮かんだ絵

後日のこと

これを書いてから約一か月後，ここでの議論の反対に見えるかもしれない

機械と人間は違うか？ - A^* と A^∞ - 2020 年 1月 15 日 (水)

を書いてしまいました．そちらはここの続きですので，こちらにご興味があれば是非！

2020.01.15 (水)

目次へ

説明における人型アイコンの効果の実験

2019 年 12月 14 日 (土)

最近，このコーナーに書いている話も随分長かったり，重かったりするものが続いているような気がするので，今回は軽いものにとどめておこうと思います．この次の話も長くなるんじゃないかと予想しますので（次は AI についての予定です）．

一般に数学や計算機科学などで，複雑な概念を理解するのに，その概念に関する構成図などがとても役に立ちます．その概念がどんなコンポーネントからできていて，それらの関係はどうなっているかなどを文章から読み解き，心の中にイメージを描く助けになるからです．

では，説明しようとする概念と直接関係のない，人型のキャラクターのような絵（ここでは，「人型のアイコン」と言っておきます）は概念の理解に役にたつでしょうか．私は，こういうのも，モノの理解に役立つと思います．

ということで実験をしてみましょう．説明対象として，１つ前のメモに載せた「エラトステネスのふるい」を使ってみます．

まず，文章による説明だけのバージョンです．

次に人型のアイコンを使ったバージョンです．

少し，説明されている気がして，聞こうという気になりませんか？

さらにセリフの部分を絞り込んでみます．

逆にセリフを極端に多くしてみます．

こうなってくると，読者は，「実は文章を読ませられているんだな」ということに気が付いて，人型のアイコンの効果は薄れていくと思います．

上の実験は非常に公平性を欠き，かつ，不十分な実験だったと思います．一般にこの手の実験はとても難しく，また，たくさんの被験者を必要とします．だいぶ前に，映像が学習にどのような効果があるかという研究のサーベイを見たことがあります．

中島義明　：　映像心理学の理論, 有斐閣, 2011 年

この本は，映像が人間によるモノの理解にどのような影響があるかに関する色々な理論のサーベイが載っています．ここでは映像は，動画だけでなく静止画も含んでいるようです．

その本に載っていたことですが，発表された論文によっては，ある研究では映像が効果的であるという結論を導き，別のある研究では効果がないという結論が導かれているなど，正反対の結果が得られているものがたくさんあるということです．どれも実験で出された結果なのですが，実験の前提条件を揃えることがとても難しいのでこのような状況が生じているようです．また，「理解に効果がある」という指標も正確に定義することがとても難しいんだと思います．

今回は「軽いメモ」ということでしたので，ここでこれらに深入りするのではなく，関連する項目のメモを列挙して終わりにします（上にあげた本とはあまり関係がなく，私がいろいろな本を読んだり，人と話して感じたりしたことです）．

プレゼン資料における人型アイコン
一般にプレゼンテーションの資料で，人の絵を使うことは，そこに注目させるのに効果があるようです．ただし，写真を使うことはしばしば逆効果だそうです．あまりにそこに気を引き付けすぎて，プレゼンの内容を理解する作業を妨害するようです．
大学生用の学習書におけるマンガ
某出版社のシリーズで，大学の数学，物理学などに関して，「マンガで学ぶ〇〇〇」みたいなものがあります．また，ほかの出版社でもマンガで高等教育の題材を扱ったものが結構増えてきたなと思います．それらは長所と短所の両方の面があるのかなと思います．良い点としては，とっかかりとしてはなんとなく優しそうな気がするので多くの人に学問の門戸を開くということで，短所としては，次のような点があるのかなと思っています．
1. マンガと本論がそれほど融合していないように思います．結局，マンガでは学問の本質には触れずに，マンガの間にある普通の教科書的なページでその学問の内容について説明をしてあることが多いようです．
2. それらの本では，人を引き付けるのに，「萌え」とか「恋愛感情」を使っています．それらは人を協力に引き付けるのだけど，同時に心の中のリソースを消費してしまいます．人間が次世代に子孫を残す欲求はそれほどに強いのですから．結果として，本来の学問の理解に使われる心的リソースが少なくなってしまい，逆効果になってしまいます．読み始めると，次第に，恋愛物語部分だけを追っていくことになり，勉強にならないとか．
3. 結局，その学問部分の執筆者とマンガの担当者がそれぞれ頑張ってしまうと，一冊の本としては２つの部分が泣き別れしてしまいます．やはり，双方で邪魔しあうのではなく，融合された内容にするように協力していくことが必要です．
一般的な原理は確立しにくい
種々の，映像が理解に及ぼす影響の実験から相反する結論が導かれていることからもわかるように，そうとう前提条件を特定しないと同一の結果は得られないように思います．その意味で一般的な原理は，「そういう場合もある」というノウハウとしてとらえる必要があるでしょう．一方，かなり特定の場面や用途を指定すれば，それなりに確度の高いルールとして使えると思います．例えば，上にあげた「エラトステネスのふるい」の３番目の例で，人型アイコンに sqrt(N) の部分への言及だけ発話にしたものは，図などのある特定の部分へ注目を集めるのに有効と言えるように思います．
学習促進に POP 広告（Point of Purchase）が使えないかな？
POP 広告とは，お店などにある，カードに書かれた広告です．「全米が泣いた〇〇〇」とか「だんなに『シャンプー変えた？』と聞かれました！！」とかです．この学問を習得したらどんなによいか，そして，この本だとどれだけ楽にできるかなどを広告して，そこに学習者の心的リソースをつぎ込ませるとか．
・・・

今回は「軽くやる」という方針でしたので，ここらでやめておきます．それでも随分，長くなってしまった気がしますが．．．図が多かっただけですね．きっと．

目次へ

違いは，出っ張り具合？ PAD と C言語風疑似コード

2019 年 12月 9 日 (月)

私は．とあるところで，C言語の基礎を終えた大学生の実習編を担当しています．そこに来ている学生さんたちを指導して思うのですが，彼らは殆どフローチャートを書きません．

実は，学生さんたちは他の図も殆ど書きません．他の図とは，例えば，ポインタで繋がっているリストの図，データ構造の図，問題を分析した結果の何らかの構成図，また，これは図ではないかもしれませんが，日本語など自然語で解法を抽象的に書いた疑似コードなどです．また，制御フローを表す図でも，好き勝手なフローが書ける伝統的なフローチャートのほかに，構造化されたフローを書くことに特化した，構造化フローチャート，PAD図, NSチャート, HCP図などもあります．これらも書きません．

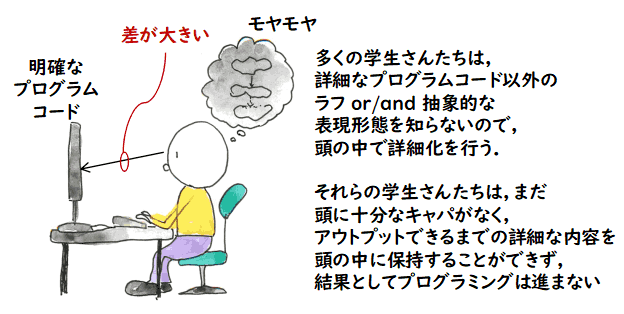
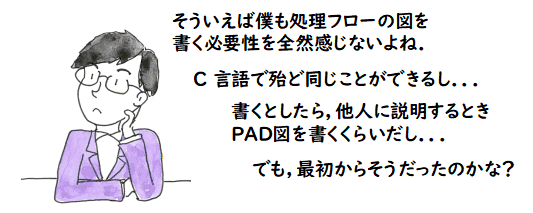
大部分の学生さんたちは，このような図を書かずに，エディタに向かって直接プログラムを書いていきます．それでプログラムが書ける学生は良いのですが，書けない学生はなかなか課題を進めることが出来ません．もしかしたら，彼らはフローチャートや疑似コードの書き方を（全く or 十分には）習ってないのかもしれません．従って，頭の中にあるもやもやっとした解法を表現する手段が，直接実行可能な詳細度を持つプログラミング言語しかないので，なかなかそういう詳細のコードを出力できずに苦労しているのではないかと感じます．私はその大学の教育全体に係わっている訳ではなく，学生さんたちがどんな教育を受けてその実習の場に来ているか知らないので，上に書いたことは想像がずいぶん混じっています．

で，これも想像なのですが，この状況は１つの大学だけの状況ではなく，全体的な状況なのではないかと思っています．理由は二つあります．一つ目は，私があまり段階的詳細化という言葉を聞いたり，目にしたりしないことです．特に本屋で「段階的詳細化」という語をタイトルにつけた本に出会った記憶がありません．こういう構造化フローチャートの技術とか，段階的詳細化の技術は殆どロストテクノロジーと化しているような気がします．

二つ目の理由は，自分自身の心の中を覗いて思うのですが，私自身がフローチャートを書かねばならないというニーズが殆ど無いことです（他の構造化フローチャートも同様）．C言語は，ほぼ構造化された疑似コードと変わらず，（私たちは）これを使って段階的詳細化が行えるので，特にフローチャートを起こす必要性を感じないのです．これは一般の先生方も同じなのではないでしょうか．先生方も，自分たちの成長のある時期までは，フローチャートや疑似コードなど，何らかの中間的な表現手法でプログラムを作成する技術を学んだと思うのですが，

彼ら自身，すでにそのような中間的な表現形態が必要なくなっていることと，
プログラミング言語が段々高級になって来て日常語に近くなっていること

とで，学生さんたちの苦労が分からなくなっているのではないのかと勘ぐってしまいます．

で，今回のメモの内容は次の二つです．

段階的詳細化などの技術の「再」活用
現在殆どロストテクノロジー化している段階的詳細化などの技法を教育に復活させた方が良いのではないか？
PAD 図と C風疑似コードの違いはどれほどか？
色々な構造化フローチャートがある中で私が使うとしたら PAD 図なのですが，これは構造的には C 言語を連接，条件分岐，繰り返しに限定したものと殆ど変わりません．したがって，自然語を使ったC言語風疑似コードで同じ内容が書ける訳ですが，PAD 図とC言語風疑似コードに違いはあるのかという疑問が湧きます．「違いがあるのか？」は何にとってを明確にすべきでしょうから，ここでは，
「プログラミング初心者がプログラムを作るときや教師からプログラミングの説明を受けるときの補助資料としてPAD 図とC言語風疑似コードに違いはあるのか
という疑問にしておきます．

段階的詳細化などの技術の「再」活用

「段階的詳細化法」とは，1960年代後半から1970年代，もしかしたら，1980年代の初めくらいまで，提唱され，使用されていたプログラム作成の方法で，最初から詳細なコードを書くのではなく，ラフな手順の記述からはじめて，次第に詳細化していくものです．技法の名前のままですね．最初に提唱されたころの代表的な文献は

Niklaus Wirth (1971), Program Development by Stepwise Refinement, 14, pp. 221-227
E.W.ダイクストラ, C.A.R.ホーア, O. J. ダール『構造化プログラミング』野下浩平訳、サイエンス社、1975年。

といったものだと思うのですが，人によって，例えば，「入力・変換・出力」の形式のプログラムと合わせた技法になっていたりとか，分割・統治の技法と合わせた技法を強調する人とか，種々の流儀があるように思います．こういう細かな流儀が色々出て分かりにくくなったことと，必ずしもすべての場合でうまく行く訳でなく，巨大なプログラムでは往々にして，データ中心の分析技法やオブジェクト指向に基づいた技法の方が良かったりすることから，段々，人々の口に登らなくなってきたのかなと思います．

こういった短所はあるのですが，しかし，小規模なプログラムで限定的に使い，「一度に詳細化せずに段階的に詳細化する」くらいの緩い原理として使う場合は結構有効で，教育においても初期段階から使ったら良いのになと思います．実際，私は全然課題を進められない学生には，

まず，日本語か，自分の得意な言語で，大まかに解法を箇条書きで書いてごらん

と勧めています．その学生が書いたものを見ながら，

まずは，この位の詳細さで書いたら良いよ
ここは１つにしないで２つのステップに分けて書くと分かりやすいでしょう
ここに書いたこの情報を保持するための変数がいるから，ここにメモ書きしておくと後で役に立つかも

とかの指導をします．あまり分かってない学生さんはなかなかアウトプットが出てこないので，どこが分かってないか分かりにくいのですが，こうして無理やりにでも書かせると，

ああ，ここがまだ一塊のままで，中がどんな手順になるか見えてないんだな

とか，分かって来るのです（私も学生さんたち自身も）．

段階的詳細化をこういった個人の工夫で使っている場合は結構あると思うのですが，我流なので，何か標準的な方法／記法があると良いと思います．次のトピックスの PAD のように，それほど難しくない大らかな技法として．

でも，こういう技法の制定はすぐ詳細化・特殊化してきてしまうんですよね．技法の開発者さんとか標準化屋さんは，何かを詳細に決めていくのが自分の価値だと思っているので．

それと，「今更，段階的詳細化か」ということで，研究者があまり飛びつきにくいトピックスであることも，この標準的な手法が確立されない理由なんでしょうね．あまり，論文ネタにならないとかで．

PAD 図と C風疑似コードの違いはどれほどか？

PAD (Problem Analysis Diagram ) は H 製作所が開発した構造化フローチャートです．世の中に既知の事実なので，別に社名を伏字にする必要は無いのですが，私の昔いた会社なので，なんとなく，直接書くのが躊躇われました．最初に PAD に出会ったのは 1982年頃，私が修士１年の学生だったときに，ある研究会で，当時，H 製作所のＦ村Ｙ彦さんという方が紹介したときだったと思います（Ｆ村Ｙ彦さんは，Wikipedia によると，後に早稲田大学の教授になられ，さらにその後ご自分で会社を作られているようです）．

なんか，見るからに怪しそうな風貌と言動のＦ村Ｙ彦さんが

PAD の普及のためにあちこちで講習会の講師をやっているんですけど，時々，「その書き方は規格と違います」と逆に注意されるんです．
もともと，私たちが作ったのに，規格化されると，もう私たちの自由にはならないんですよ．

とか言われていたような気がします．当時の私は，「へー，真面目そうな企業の社員なのに面白い人だな」と思った記憶があります．

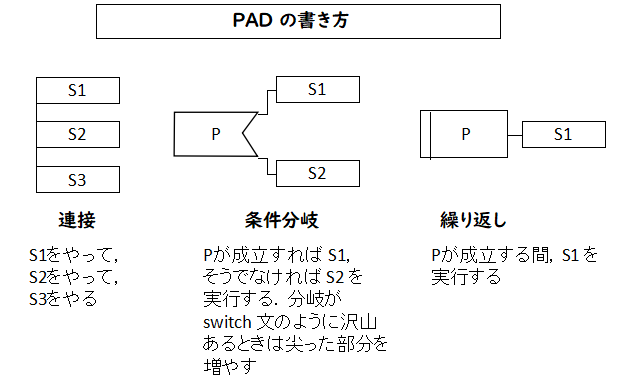
PAD 自体はかなり簡単で，基本的には次の３つの規則を覚えておけば書けます．これらは構造化プログラミングの３つの要素ですね．

連接
逐次的に実行する動作を縦に書いていく．
条件分岐
条件が成立するときの動作としないときの動作を書く． C 言語のswitch 文のように多くの条件を書くことも可能．
繰り返し
ある条件が成立する間，ある動作を繰り返すことを書く．

他にも規則は沢山ありますし，流儀も沢山あるように思いますが，私は，上の３つを使い，箱の中に適当な自然語を入れて使っています．

皆さんもお分かりと思いますが，実は，PAD で書いた殆ど同じものが，C 言語で書けるのです．要は PAD は C 言語の構文木をグラフィカルに書いているだけですから．

例えば，「エラトステネスのふるい」で N 以下の素数をすべて列挙する手順を C 言語風疑似コードと PAD で書いてみます（小さい数からはじめて，見つかった素数の倍数を消していって残ったものが素数という方法）．

まずは，C 言語風疑似コードです．

C言語風疑似コードによる「エラトステネスのふるい」の手順

続いて，PAD です．

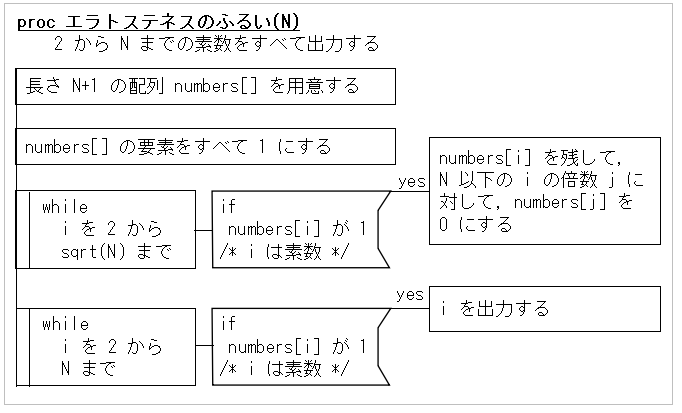PADによる「エラトステネスのふるい」の手順

多少，視認性が違うような気がします．私は，この二つの効果が，学習者や，これを参考にしながらプログラムする人にとって，本当に違うのかずっと悩んでいました．もっというなら，現在進行形で悩んでいます．これら二つはロジカルには等価なものを書いているつもりだからです．書いたり，修正したりは，C言語風疑似コードの方がはるかに簡単です．でも，初学者に見せたとき，どちらが分かりやすいかと言うと PAD 図の方が分かりやすいのではないだろうかと思いますので，学生さんたちに説明するときは， PAD 図に落とすようにしています．もしかしたら，PAD 図はフローチャートほどは一般的ではないので，学生さんによってはこの図を読めないかもしれないという心配はありますから，有難迷惑なのかもしれませんが．一応，凡例はつけているので，それを見て解読はできると思うのですが，そういうことを総合すると，C言語風疑似コードに理解容易性において劣るかもしれません．

いろいろ，あーでもない，こーでもないという議論をしてしまいましたが，現在，私の中では，

これら二つの同値な図は，学習者の受け取り方は違うだろう
PAD の読み方を覚えたものにとっては，一般にはPAD の方が把握が容易だろう（人のタイプによるとは思うのですが，文章より図による把握の方が得意な人の方が一般的には多い）

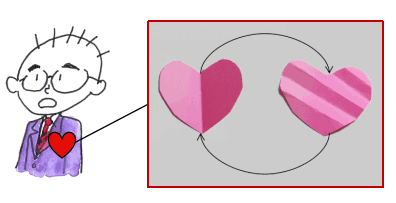
という重みづけをしています．そして，ロジカルには同じなのだが，受け手の印象が違うということの納得のために，次のようにトポロジカルには同じ絵なのだけど，受け手の印象の違うものは世の中に沢山あると考えるようにしています．まあ，安心のための比喩だけですが．

さらに，色を加えるともっと印象が変わります．

また，PAD 図とC言語風疑似コードとは出っ張り具合が違うということに着目するなら，横顔の対比の方がよいかもしれません．

つまり，疑似コードに比べての，PAD の極端な凸凹，四角の区切り，文章と if や while などの構文要素の明確な分離は，人にその処理フローの特徴をかなり明確に印象付けるものではないかということです．

ということで，プログラミングや計算機科学，数学でも，ロジカルには一緒でも印象が違い，学習効果が異なる教具が存在し得るという個人的な結論を出して，今回のメモは終わりにします．

けど，．．．

追加事項 -- goto のこと --

最後にもう一つ．最近の学生さんがフローチャートを書かないことに関して，もう一つ気が付いたことがあります．最近の学生さんは，goto も殆ど使いません．もしかしたら goto を習ってないのかもしれません．学生が goto を使うのを見た数少ない例では，その学生はどちらかというと優秀な学生でしたから，自分で習得したのかもしれません．フローチャートからプログラムを起こす場合は，goto がある程度出てきますから，フローチャートを書かないことがこれに寄与しているのかもしれません．goto は，エラー処理など，ある局面ではプログラムを分かりやすく書く効果はありますが，一般的には処理の流れを分かりにくくするので，殆どの学生が goto を使わないという状況は，今の教育は構造化プログラミングの普及に成功しているのかもしれません．ただ，上にも書きましたように，これは図を排除することが良いと言っているのではありません．フローチャート以外の図や何か詳細なものに落とし込む手前の表現形態を勉強させることは初学者の躓きを無くすことにつながると思います．

おまけ

学生さんたちがあまり図を書かないのは，いったん図を起こして（b），そこからプログラムを作る方(a)が，直接プログラムを作る(c)より手間がかかると思うからなんですよね．「三角形の二辺の和は他の一辺より長い」ですね．でも，c が絶望的に出来ないときは，a + b の方が短い訳で．急がば回れなんですよね．

近くに見えても，思ったより遠い

目次へ

学習形態に関するメモ：プレゼン資料の提示形態

2019 年 12月 4 日 (水)

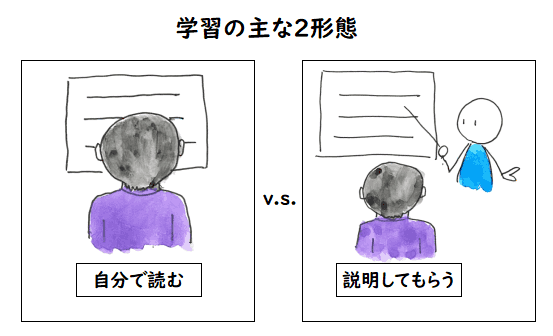
学習というような大げさなものではないかもしれませんが，プレゼン資料を自分で読むか，相手に説明してもらうかで，理解の程度に差があるように感じますので，今回はそれについて考えたことを書いておきます．あまり整理されていないのですが，追々，整理していきたいので，忘れないうちに考えたことを書き下しておこうということです．「難しいことを比較的容易に理解するためにはどうすればよいか」というのが私の重要な関心事だから，こういう思い付きは大切なのです．

私は，とある勉強会に時々出かけるのですが，発表資料が事前に PDF でその会の web-site に掲示されるので，それを読んでいきます．自分で読むのは，自分のペースで進められるのでとても良いのですが，やはり理解できないところもあります．そういうのを，実際に勉強会に行って，発表者の説明でプレゼンを一枚一枚進めていくと，自分で読んでいて分からなかったことがとてもよく分かるのです．

いま述べた例はとてもまともな比較にはなってないとは思います．例えば，上の例で発表者付きのプレゼンでは，

読むのが２回目であること
一度目を通したプレゼン資料をもう一度聞くと理解が深まるのは当然
補足説明があること
発表者はプレゼン資料に書いてないことを補いながら説明するんだろうから，より理解が深まるのは当然
質問が可能な事
勉強会では質疑応答ができ，読んで分からないことも質問すれば分かるので，理解が深まるのは当然

といったことから，発表者の説明を聞くほうが理解が深まるのは当然という議論が成り立つでしょう．

でも，私の感覚的にはそれ以上に理解が深まっているような気がするのです．また，発表者によってはプレゼンに文章を書き，それをただ読むだけという人もいますが，それでも，発表形態のほうが理解が深まっている気がするのです．

ということで，今日のメモの内容は，この「理解が深まる（と感じる）」理由はなんだろうか，思いつくもののメモを残しておこうということなのです．上に述べたような第１因子を置いておいて，第２の因子を考察するのですから，あまりまっとうな話ではありません．趣味の一人ブレインストーミングです．

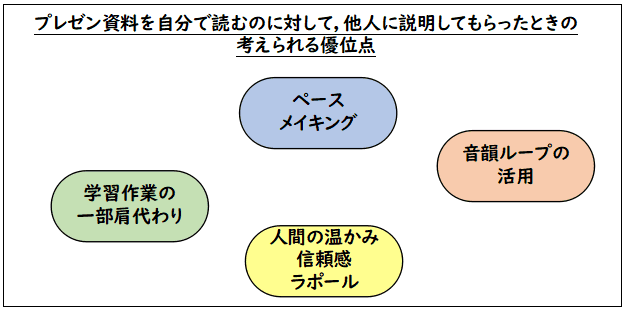
とりあえず，すぐ思いつくものを挙げてみます．

今回はこれらについて一言ずつ述べてみます．

ペースメイキング
自分で読むときは，かなり速い速度で読んでいます．早く有効な情報を得たいというあせりの気持ちがあり，結構，飛ばして読んでいるのかもしれません．それに対して，人がプレゼンするときはゆっくりした速度で説明がなされます．この強制的な速度抑制で，小部分ずつの理解がしっかり出来ているのかもしれません．
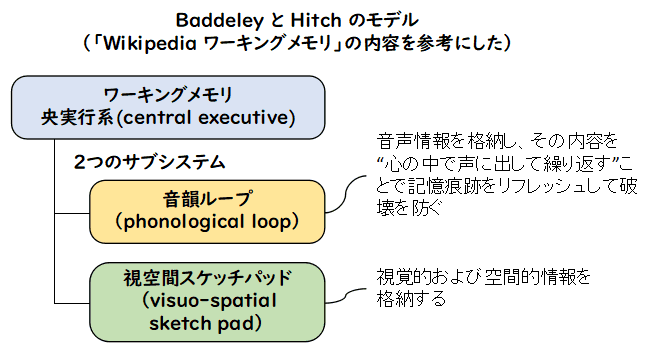
音韻ループの活用
人の説明では音声がしっかり発音されます．それに対して，自分で黙読するときは，音声がそれほど頭の中に木霊（こだま）することはありません．「音韻ループ」とは
認知科学での用語で，ワーキングメモリモデルの中央実行系のサブシステムの一つで言語・音韻情報を保持する記憶貯蔵庫

だそうです．聴覚の短期記憶です．発表者がしっかりした音声で説明してくれると，自分で読んだときはあまり働かなかった音韻ループがしっかり働いて，記憶や理解を助けるのかもしれません．発表の場合は，音声の反復を含んでいる訳ではないので，正確には当てはまらないかもしれませんが，何らかの効果はあるんじゃないかと勝手に想像しています．一方，音声を頭の中で木霊するのはそれなりの時間がかかるので，頭の中での音読は，読書を遅くする理由として挙げている人もいるようです．「速読」を主張する人とか．技術的な基礎の学習とかは，しっかり定着させることが必要なので，ある程度時間を掛けてもよいのではないかなと思います．
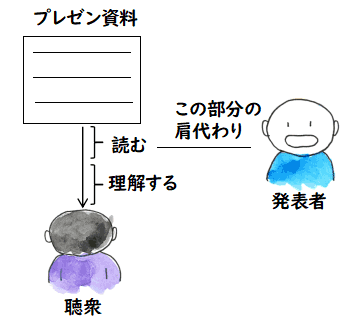
学習作業の一部肩代わり
やはり，ものを読むのはそれなりに労力が必要なのですが，音声にするまでは他人である説明者がやってくれるので，その分の頭の CPU パワーを理解に回すことができているのかもしれません．でも，音声認識の分が増えているのでこれはウソかもしれません．あっ！　テキストを読むのでも，実はテキストコードを読んでいるのではなく，画像理解でテキストコードに落としているのでしょうからどっちもどっちかもしれませんね．
人間の温かみ，信頼感，ラポール
発表者から「これは真実なので信じるように！」という一種の「霊波光線」が出ているのかもしれません．あるいは，自分自身の中に，「発表者に申し訳ないので理解してやらなければ」という気持ちが生じているのかもしれません．あるいは，この発表者-聴衆という環境設定が，知識の受け身の体制を整えて，知識が入ってきやすくなっているのかもしれません．一方，発表者がいかにもうさん臭くて信じられないと思う時は，かなり批判的な気持ちが働いて，知識はすんなり入ってこないでしょう．

私は，６年前，会社を辞めた頃，学習に，「説得術」が使えないかと考えたことがあります．無批判に何かの陳述を受け入れるのは学習とは言えないかもしれませんが，生き物である私たちが，ある種の知識を手に入れるためには，保持すべき知識を受容しないといけません．したがって，取り込みを楽にするための方便として，このような説得術に基づいた手法もあっても良いのかもしれないと思ったのです．もちろん，無批判の取り込みは良くないので，しっかり有効性を確かめたあと，それを受容し，活用する手段としてではありますが．説得術ですぐ思い浮かぶのは，
1. まず小さな要求を受け入れさせて，次第に大きな要求にしていくとか
2. 逆に，まず，受け入れられないような大きな要求を出しておいて，それを否定させておいて，実際に受け入れさせようとしている要求を出す　とか
があります．「小手先だけのテクニックで要求を飲ませるのは良くない」と言った注意書き付きですが，色々なテクニックがあるようです．こういうのもプレゼン，あるいは，学習で役に立つかもしれません．例えば，とても難しい大きな定理を理解するのに，まずは，その定理の系から導かれる小さな例題をいくつか理解してから，その大きな定理の理解に取り掛かるとかです．この例は結構普通ですね．

以上，かなり胡散臭い考察のオンパレードでした．こういう頭の中に時々思い描くことは，機会を見て言語化しておかないといつの間にかなくなってしまうので，今回，言語化してみました．

プレゼン資料からの学習形態として，他に，展示会でのパネル展示などがあります．これは置いてあるパネルを読んで，分からないことを説明者に聞くことができるので結構充実した学習ができます．時々，読んでいる最中に，説明者が，「ご説明しましょうか？」と割り込んでくることがあったり，もう読んでしまって声を掛けて欲しいのに誰も声を掛けてくれなかったりすることもあります．そこでの説明者のスキルは，お店で，タイミング良くお客さんに声を掛けることができる店員さんのスキルと共通のものがありますね．

会社を辞めてから６年間，久しくこういう展示会場に行ったことがなく，世の中に取り残されている気がするので，何か無料の展示会などを探して行ってみようかと思う今日この頃です．

目次へ

「物理学の応用について (寺田寅彦)」を読んで

2019 年 11月 23 日 (土)

このサイトの別ページで，青空文庫に挿絵を付けて紹介する（寺田寅彦の作品は，こちらで紹介）というのをやっていますが，昨日，寺田寅彦の次の随筆を紹介しました．寺田寅彦は， Wikipedia によると，戦前の日本の物理学者、随筆家、俳人（1878年（明治11年）11月28日 - 1935年（昭和10年）12月31日））です．

物理学の応用について (寺田寅彦著)

物理学は基礎科学の一つであり，その応用は，
純粋な科学の各種の方面，工業，医学，航空術，
各種殖産事業と幅広い．

そういう分野への応用を進めるにあたっての方法や
心構えについて述べた随筆．

初出：「理学界　第十巻第九号」1913（大正2）年3月1日
サイズ : XHTML版 9.8 KB

この随筆は，文字数にして 3,300文字位（４００字詰め原稿用紙９枚）の短い随筆ですが上の場面の文章がとても気に入りましたのでこちらでも紹介したいと思います．

この随筆は上の絵でも説明しましたように，物理学を色々な分野に応用していくときの，心構えや方法について述べているものですが，理論を実際の応用に持っていくときは，色々な抵抗に会うということが，この随筆の中に次のように書かれています．

複雑な実際問題を研究して先ずその真相を明らかにしようという場合には、先ずその大体を明らかにして枝葉を後にするのが肝要である。
...
渾沌とした問題を処理する第一着手は先ず大きいところに眼を着けて要点を攫むにあるので、いわゆる第一次の近似である。
しかし学者が第一次の近似を求めて真理の曙光を認めた時に、世人はただちに枝葉の問題を並べ立てて抗議を申込む。

...
第一次の近似だけでもそのつもりで利用すれば非常に有益なものである。
...

この随筆は百年以上前に書かれたものなのに，今日でもこの状況は変わってないように思います．つまり，その理論は第一次近似だと思って使えば，それなりの恩恵があるにも関わらず，色々な枝葉末節の欠点をあげつらって，適用させないようにする人たちがいるということです．研究者の中にはこういうめにあった人も多いのではないでしょうか．私もこの気持ちが分かるところを見ると，若いとき，こういうめにあって大いに憤慨したことがあったに違いありません．

ところで，同じ人がこの世人と理論適用の提案者になっていることはないでしょうか？　つまり，ある事柄については，理論適用の提案者になって，世人の態度に大いに憤慨しているのだけど，別の事柄については，世人となって別の提案者を攻撃しているとか．

例えば，私は，一つ前の日記の「仕様は実装より分かりやすいか？」で形式手法について，かなり否定的なことを書いたと思います．これは，今をさること約４０年前，1982年ごろ，大学の研究室で作っていたプログラムの検証システムの経験がトラウマになっていることがあります．私も少し作ったのですが，大部分は私より前の学生さんや先生が作って，私は主に，このシステムを使ってその妥当性を調べる役割でした．

そのシステムでは，プログラムが満たすべき性質や補助的な情報を一階述語論理で与えると，証明すべき一階述語論理の論理式を生成して，後は，そのシステムに備わっている証明システムでひたすらその論理式を証明するというものでした．

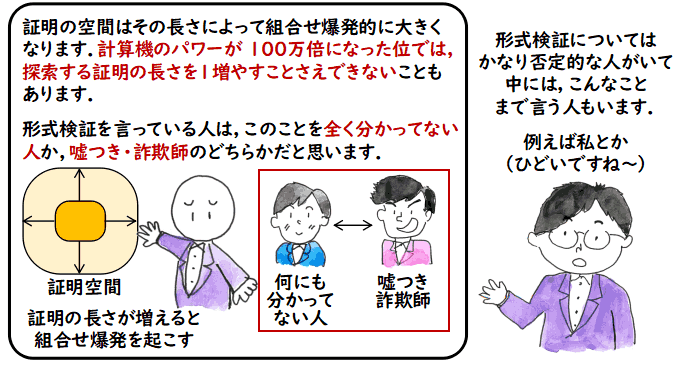
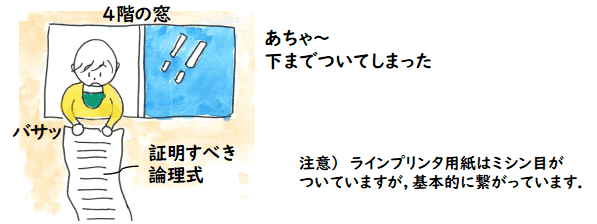
ほんの小さなプログラムでも証明すべき式はすさまじく大きくなります．そこの建物は４階建てでしたが，ラインプリンタ用紙にその論理式を打ち出して，４階の窓から垂らすと，きっと下までついてしまうほどの論理式を相手にしないといけないのです（ラインプリンタ用紙は一ページごとにミシン目がありますがずっと繋がっています）．

論理式の一部分には x=x のような自明な論理式も含まれているので，そういうのを除去するとある程度までは小さくなるのですが，それでも量に圧倒されます．そのとき，証明の空間を直に感じとったのがトラウマになっていて，形式検証にちょっと否定的な気持ちが出てきてしまうのです．もちろん，計算機も当時から比べるとすさまじく良くなったのですが，やはり，証明の空間は莫大です．ちなみに，これはAI（人工知能）にも絡んだ問題だと思います．人は証明空間に均等に関心を持っている訳ではないので，何か人の活動に関連の深い部分空間に限定する方法はあると思いますが，何となく私はこの広大さに恐れがある訳です．

形式検証にしてもAI（人工知能）にしても，その発展のどの段階でも，（人と言うお手本の）第一次近似だと思って，欠点に目を瞑れば，色々役に立つことが多いと思います．寺田寅彦の随筆では先の文章の前に次のようなことが書いてあります．

今一般に実際上の問題に物理学を応用しようとする時に、第一着手としてしなければならぬ事は問題自身の分析的研究である。
実際上に起る問題をちょっと見ると簡単なようでも通常非常に複雑なものである。
同時に範囲の判然せぬ問題が多い。

「問題自身の分析的研究」，たぶん，問題自身をきちんと分析してどこまでを解決するのか／できるのかということに見通しを立てる必要があるということなんだろうと思います．よくよく考えてみると，私もあまり良く考えずに，「こんなことができる，あんなことができる」と言ったことがあったと思います．

そしてやっていくうちに何とかなると思っていた問題が実はとても難しい問題で最初のセールストークからずいぶん後退したり，あるいは結局，使い物にならなかったり．

予算を取るときは，あまり欠点を大きく言うことは得策ではないし，プレゼン相手を混乱させてしまうので大っぴらには言えませんが，トーンの大小や言い方を工夫して，やはり，こういう，出来ないことや欠点も一応分析して述べておかないといけませんね．

今回は理論を適用する提案者側とそれに反対する世人の両方に配慮したバランスのとれた，我ながら良いお話になったのではないかと思います．

でも，他人の提案に枝葉を並べたくなる心理は，人間の根源に係わる何か（生存競争に係わる）かもしれないので，今度，枝葉を言いたくなった時には自分の心の中に潜ってみたいと思います．自分たちが生き物だと言うことを忘れて，理想を語ることはできませんので．

目次へ

仕様は実装より分かりやすいか？

2019 年 11月 16 日 (木)

ソフトウェアの分野で「形式手法」という研究テーマがあります．ソフトウェアの信頼性を向上するために，仕様を述語論理や様相論理などで「形式的」に記述して，実装がその仕様を満たすことを，証明やモデル検査などで確かめる（検証する）という研究テーマです．検証まではやらなくても，とにかく「形式的」に仕様を書いてみるというようなことも含むと思います．ここで「形式的に」というのは述語論理など形式的体系を使って厳密に記述することを意味します．私の知り合いにも，形式手法に真剣に取り組んでいる人がいます．

ここでは，証明やモデル検査などの難しい話ではなく，

そもそも，仕様は実装より簡単にかつ明瞭にソフトウェアを記述できるのだろうか？
あるいは，これは仕様，あれは実装のように明確に区別がつくのだろうか？

ということを考えてみたいと思います．もっと言うなら，仕様と実装の間の理論的な線引きはとても難しいということを言うつもりです．

一般には，仕様自身はソフトウェアが動くところまで書かなくて良いので，記述において動くための仕掛けを省略して，そのソフトウェアが満たすべき性質，あるいは他のモノ（ソフトウェア，デバイス，etc.）との関係のみに着目できます．

その意味では，

その具体的な効果として

記述が少なくて済むという効果も得られます
これにより，人間が読みやすくなり，仕様の段階での誤りも発見しやすくなるでしょう．また，実装が仕様通りかを調べるときも，テスターが仕様を十分把握していることが必要です．これにも寄与します．
余計なことを決めすぎないで良いと言う効果も得られます
実装では動作を可能にするために，本来，利用者側からは要求されないことまで決めていることがあるのです．仕様ではそれを削除して実装に自由度を与えることができます．

今回の日記では，

これらのことは本当なのか？
もしかしたら，我々が心の中に抱いている幻想，あるいは，願望にすぎないのではないか？
また，もし，本当なら，その線引きを可能にしているのはいったい何なのか？

ということを考えてみたいと思います．

少し話の設定を設けておきます．それは仕様と実装を記述する言語を別のものにしてしまうと，話が簡単になりすぎてしまうからです．例えば，Ｃ言語で書くのが実装で，述語論理で書くのが仕様というような基準ができてしまいます．ここはどちらも述語論理にしてしまいましょう．述語論理でも Prolog のようにホーン節だけに限れば，インタープリタを用意して，実装が書けます．つまり，フルの述語論理を使うと性質の記述だけになってしまうが，その中のある部分集合に限ると実行できるという記述体系の中で考えることにします．

この枠組みでも実行できないものを実装とは呼べないでしょうから，たまたまホーン節で書けて実行できるようになってしまったものを実装と呼ぶべきか仕様と呼ぶべきかが問題になります．

話を少し具体的にしていきましょう．配列のソートを考えてみます．配列の要素は大小関係のあるキーを持っていて，入力の配列のキーはすべて異なっているとします．そうすると仕様は次のようなものになるでしょう（読みやすさのために厳密な文法は決めずに書いています）．

b = sort(a) →
b は a の要素の並び替え and
(0 ≤ i < j ≤ size(b) → b[i] < b[j])

つまり，

配列 a をソートした結果の配列 b は a の並び替えであって，要素の小さいものから大きなものへの順序で並んでいる

ということです．

この記述は，ソートするとき，どのような手順で要素を並び替えるかという情報を含んでおらず，ソートされた結果に要求される必要なことだけを含んでおり，大変分かりやすく感じます．具体的にどうやって並び替えるかは実装者に任せられ，バブルソートでもクィックソートでもマージソートでも適切に選んで実装すればよいのです．

この例を見る限りは，仕様は非常に分かりやすくソフトウェアの記述や検証にも有用に思えます．しかし，ほんの少し条件を複雑にすると状況はがらりと変わります．

上のソートの例で次の二つの条件を付け加えてみましょう．

キーがすべて異なっているとは限らない
ここでは要素のデータ自体は異なっていると仮定します．これは，単にキーの選び方が不適切ということかもしれません．
以前のソフトウェアで出力されていた順番を守って欲しい
キーが同じでデータは異なる場合はキーの部分がソートされた色々な要素の並びが考えられます．クィックソートやバブルソートなど，ソートのアルゴリズムはキーが異なっていれば結果は一緒ですが，同じキーがある場合は，一般には結果の並べ方は異なります．例えば，ここで対象となるソフトウェアは以前のソフトウェアのバージョンアップで，以前のソフトウェアはある種のクイックソートを使っていたとします．

実は，こういうことは現実にあり得ます．例えば，ある店舗の顧客の集合から色々な観点で抽出したリストを作るようなソフトウェアでは，以前の並びと微妙に異なる順序のリストを受け取った担当者は嫌がるかもしれません．セカンダリのキーを決めていなかったということが悪いのかもしれませんが，既存のシステムの中にはこのようなものは結構あるのではないでしょうか．

これは，システムの刷新に伴ういくつかの一時的な不便は我慢すると言う，責任者の英断がないと何時までも古いままになってしまうのですが，過渡期にはあり得る話です．

このような条件にすると，ソートの仕様としては，上のようなすっきりした仕様でなく，元のソフトウェアのある種のクィックソートの並びを規定したソートの仕様を書かなければならなくなってしまいます．クィックソートは，適当に選んだ要素を基準にして，それより大きな要素のリストとそれ以下の要素のリストに分けるということを繰り返していくソートですから，同じ順序（同じキー）のデータ同士の相対位置は動的に変わってしまいます．これを最初の配列の性質から静的に論理式で記述するのはとても難しく，元のソートのアルゴリズムをそのまま論理式（ホーン節）で記述するしか無いように思います．以上，例題がちょっと長かったですが，これは

仕様として，アルゴリズムを記述し，しかも動くレベルまで記述しなければならない例で，仕様が実装より簡単にすっきりと書けるとは限らないことを示す例

でした．

もう一つ，簡単な例として，例えば，信号機の色の変わる順番を規定する仕様を考えてみます．信号機の色が，青 → 黄 → 赤 → 青と変わるという仕様は，

next(青, 黄)
next(黄, 赤)
next(赤, 青)

となるでしょう．実はこれは動いてしまいます．したがって，前の例もそうですが，動く動かないを実装と仕様の差にすることはできません．

以上をまとめると次のようになります．

仕様と実装の違いを，動かない，動くで規定することはできない
ある記述が仕様か実装かの違いは，そのソフトウェアに対する人間の頭の中にある要求を表したものかどうかであって，動かない，動くのような単純な基準で定義することはできそうもありません．でも，こういう頭の中のモヤモヤとしたものを理論的な違いとして規定していくという活動自体は大切なことだと思います．
記述の対象によっては手順を記述してしまった方が，楽でかつ理解しやすいこともある
必ずしも，手順（アルゴリズム）から離れた記述が分かりやすいとは限りません

以上，仕様と実装の違いを改めて考え直してみると言うお話でした．仕様というのはソフトウェアを作る人が，作るべきものを必要十分に記述したもので，実装はそれを満たす実際に動くものということなのでしょう．そして，仕様が実装より分かりやすく書けることが多いというのは仕様を作る人たちの努力と勇気によってそうなっている部分も大きく，仕様だから，実装だからだけの理由では無いと思います．

こういう，概念の区別に人間の判断基準や感性が絡むものは，理論的かつ厳密な定義が難しいのですが，やはり，定義しようという努力はそれらに対する理解を深めることに繋がり，大切なことだと思います．こういった事例は沢山あると思います．例えば，

特許で，「発明」と「単なる既存の技術の組み合わせ」の違いは何か？

* 青空文庫海野十三の作品紹介ページ「特許多腕人間方式」を参照
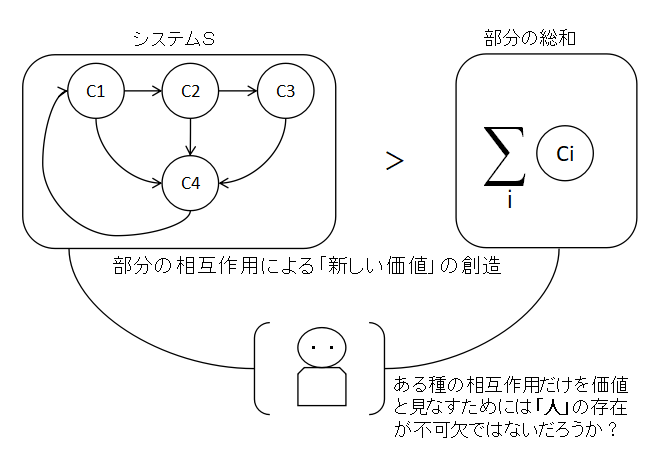
システムの理論で，「システムとはそれの部分の算術的総和以上のものである」という人がいるが，「単なる部品間のインタラクション」と「算術的総和以上のなにか」は違うのか？
「感覚的なもの」は「内容」を変容させて，新しい創造的な価値を生むか？製本，表現形態，創造，ついでに，システムにおける人間の寄与
に関連事項
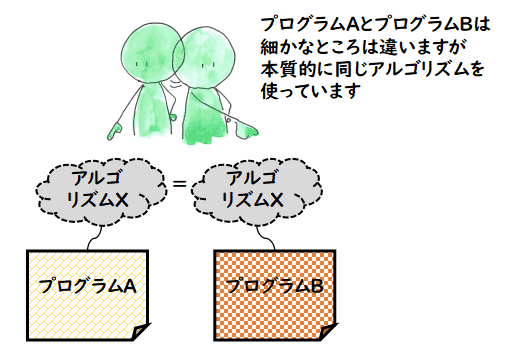
計算機科学で，何が「プログラム」で何が「アルゴリズム」なのか？
「アルゴリズム」とは何だろうか？
に関連事項