 そんなとき,学習している理論を
そんなとき,学習している理論を(Simple Operator Precedence Parser in Ruby)
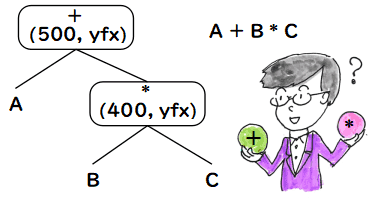
計算機科学の分野の人は,様々な計算機理論を勉強するのに,やっぱり,
学習していることを実際に
 そんなとき,学習している理論を
そんなとき,学習している理論を
で,そういった理論の実装をしてみるのでも,例えば,LISP や Ruby のリストや配列を
使った内部コードっぽい式では
気分がでないので,何となく
ということで,ここでは,計算機数学の理論をちょっと実装して楽しむときに 使えるような超簡単なパーサーを作ろうと思います. 計算機(主にソフトウェア)の話題 で 前に取り扱ったλ式をコンビネータ論理に変換する話なんかも,こういう パーサーが用意されていたら,もう少し簡単に出来たかもしれません.
ここで作るパーサーは
以下,パーサーの方針,簡単な解説,注意事項,プログラムリストと続きますが,あまり御託を 読みたくない人は,プログラムリストに飛んでもらっても 構いません.
また,この簡易パーサーのプログラムは一般的なものなので, 特に私が権利を主張するようなものでもないので自由に 持って行って改造して使って構いません.ただし,私が使う権利を はく奪する形で権利を主張するのはやめていただきたいです. こまかな注意事項は,注意事項に書きました.
この簡易パーサのデモと簡単な説明のYoutube 動画を作りました. 2022.08.05簡単な演算子順位法によるパーサー in Ruby - 概略と実行方法の説明 - ... 36分 11秒

デモプログラムの動かし方と演算子の定義方法の概略を説明しています.22分位までが,デモプログラムの動かし方と,動かした結果の説明です.その後,演算子の定義方法などを説明しています.
簡単な演算子順位法によるパーサー in Ruby - 字句解析についての説明 - ... 18分 52秒

掲載しているプログラムの字句解析が分かりにくいと思ったので,その解説です. 2022.08.11
ここに挙げた構文解析プログラムは,出来るだけ簡単で,しかも,十分に計算機理論の学習に利用できる 構文解析プログラムを作ろうという方針で作りました.
具体的には次のような方針で作りました.
後日追記:2019.2.26 これは次のようなおもちゃを作りました.
例えば,(a+b)* を有限オートマトンに変換するなどです. 適当な定義のもとに,ここのパーサーを使えば,(a+b)* は,ruby の 配列 [:"*", [:"+", "a", "b"]] に変換されますので,オートマトンの 教科書などをみながら,これを受理するオートマトンを作ってみるのは 良い勉強になります.
実際に作成した結果としては,演算子の定義,式の表示関数, テスト用のプログラムを含めると250行くらいになりましたが, 構文解析部分だけなら 200 行に納まりました(160行くらいですね. 2019年 2月 10日 時点).
追記:構文解析部までなら 160 行位なのは変わりませんが,式の表示機能を 強化したので全体で300行ほどに なってしまいました.申し訳ないです. 2019年 2月 23日
内容
まず,演算子順位文法とはどんな文法かと言うことを簡単に説明しておきます. ここで掲載するプログラムは,典型的には
ここでは2項演算までを考えることにします.以下,文法そのものの説明でなく, そのような文法で表すことができる言語について説明します.大雑把に言って, 二項までの演算子を使った演算子優先順位文法では次の BNF で生成できる ような言語を表現できます.
Exp ::= BasicToken |
PrefixOp Exp |
Exp PostfixOp |
Exp InfixOp Exp |
( Exp )
ここで BasicToken は予め定められた Exp になるデータがあると思ってください.
実際のプログラミング言語では,数や文字列などの定数とか,変数名とかがこれに
あたります.また,PrefixOp は前置される演算子,PostfixOp は後置される演算子,
InfixOp は中置される演算子を表し,予めどんなものがあるかは特定されているとします.
この文法は曖昧性を持ちます.例えば,op が二項演算子,a が BasicToken とすると, a op a op a は,(a op a) op a とも解釈されるし,a op (a op a) とも解釈されます. 演算子順位文法は演算子の優先順位という概念を 使って,この曖昧性を解消できる文法です.例えば,普通の加減乗除を使った式では 掛け算が足し算や引き算より結合力が強いとして扱われ,例えば
(x*(y+z)*w や x*(y + (z*w)) などではなく)
などの結合の型を指定することにより,パーサーに構文解析の方法を指示するタイプの パーサーを作成します.
言語は Ruby を使って書きます.文字列の式は Ruby の配列などのデータに変換することに します.例えば,上の例でいうと,下に掲載したプログラムを使うと
変換されます.つまり,
や
非常に大雑把な説明でしたので,演算子順位文法,演算子順位法の構文解析に ついて正しく知りたい人は参考文献に挙げてある文献等 を参照してください.
ここで作る演算子順位パーサーでは,
まず,演算子の定義について説明します.
後に掲載しているプログラムリストから,それら二つの定義部分を抜き出してみましょう. これは演算子定義のサンプルのために最初から入れてある演算子定義です.これを 書き直すことにより,自分が望む形の式を構文解析できるようになります.
いまから作るパーサーは,Ruby の大域変数 $sop_ops に連想配列(ハッシュ)として 演算子を定義することにより,その演算子を使った式が構文解析できるようになります. 例えば,定義の最初の方をみると, 演算子 "->" は優先度 1000 で,右結合的な演算子 (:xfy) として定義されています. これは,
[:"->", "A", [:"->", "B", [:"->", "C", "D"]]] のように構文解析される
$sop_ops = {
# in_name => [out_name, priority, op_type]
:"->" => ["->", 1000, :xfy],
:"*" => ["*", 400, :yfx],
:"/" => ["/", 400, :yfx],
:"+" => ["+", 500, :yfx],
:"+/pre" => ["+", 200, :fy],
:"-" => ["-", 500, :yfx],
:"-/pre" => ["-", 200, :fy],
:"=" => ["=", 1500, :xfy],
:";/post" => [";", 1800, :yf],
:";" => [";", 1800, :yfx],
:"," => [",", 1400, :xfy],
:"#apply#" => ["#apply#", 1300, :yfx], # implicit operator
:"#list#" => ["#list#", 200, :fy], # list marker
:"#set#" => ["#set#", 200, :fy], # set marker
# paren =>
# [out_name, priority, paren_type, [pair_paren, ...], valOf(), marker
:"(" => ["(", 10000, :open, [:")"], "0", nil],
:")" => [")", 10000, :close, [:"("]],
:"[" => ["[", 10000, :open, [:"]"], [], :"#list#"],
:"]" => ["]", 10000, :close, [:"["]],
:"{" => ["{", 10000, :open, [:"}"], :"empty", :"#set#"],
:"}" => ["}", 10000, :close, [:"{"]],
}
:"->" の後ろに :"*" があります.こちらは,優先度 400 で型が左結合的 (:yfx) の 演算子であることを表しています.優先度は少ない方が強く結合すると解釈します. ここらあたりは,論理型言語 Prolog の方式を採用しており,一般の演算子順位文法の 優先度とは大小が逆かもしれません.とにかく,ここでは数値が小さいほど結合度が強く, 数値が大きいほど結合度が小さいと解釈します.したがって,
演算子は連想配列(ハッシュ) $sop_ops の中で次のように定義してください.
内部名 => [外部名, 優先度, 演算子型 [, 表示名] ],
この一番最後の
:"+" => ["+", 500, :yfx],
それぞれの項目について説明します.
下に掲載したプログラムやここの説明の中では,内部名は Ruby のシンボルを 使うようにしています.これは別に文字列にしても構いません.演算子定義の 大域変数 $sop_ops における定義で内部名を文字列にしてしまえば,構文解析した 結果も演算子は文字列になります.これをシンボルにしたのは,構文解析した 結果を使う時の効率の観点からです.以下,その理由を正確に書きますが, Ruby のシンボルと文字列について詳しくない人,シンボルでも文字列でも 使えればどちらでもよい人は飛ばして構いません.
方針に書いたように,構文解析については
それほど効率を重視しないことにしましたが,構文解析した結果をユーザが利用
するときは,ユーザの要求に応じて効率よく動作することが必要でしょう.
例えば,なにか簡易言語をユーザが作ったとして,その動作がとても
遅くなってしまうと,ユーザは悲しいかもしれません.ユーザが構文解析結果を
使う時は,演算子が何かによって動作を変える必要があり,したがって,演算子間の
比較が必要になります.もし,演算子を文字列にすると,この比較にはC言語で
いうところの strcmp() が必要になる訳です.すまり,文字列を構成する文字,一つ
一つの比較が必要になります.それに対して,シンボルは読み込みの時点で
同じ表示名を持つシンボルは同じポインタを指すようになっていますので,
ポインタの比較だけですみます.したがって,比較の実行がはるかに速くなります.
ということで,今回は,演算子の内部名はシンボルにしました.
"a + b * c" は,"a + (b * c)"と解釈されます.
これは次に示すように,f, x, y の記号を組み合わせたものです.これは
DEC-10 Prolog の演算子の表現方法を使っています.以下の記号では,全部,先頭に
: がついていますが,これは Ruby のシンボルを表す記法なので,シンボル名としては,
その後ろだけです.この中で f はその演算子自身を表します.x は,その演算子の
優先度より
こういうことです.これは,同じ優先度の演算子が同列に並んだ時に曖昧性を 解消するために使われます.上の例では :xfy の型を持つ演算子としては -> があります.今,
という並びを考えてみます.これを
(A -> B) -> C
このように解釈しようとすると,右側の -> の左側に -> と同じ優先度の 演算子の式が表れることになります.これは -> が xfy の演算子であると いう要求に反します.なぜなら -> の左側は x でそれは -> の優先度より 厳密に小さくなくてはいけないという要求だからです.一方
の解釈だと,左側の -> の右側は -> と同じ優先度の演算子が使われている式 ですが,-> の型は xfy なので,その制約に反しません.したがって, -> は同列に複数使われると右側から括弧でくくられる右結合的な演算子に なります.少し書くのが遅れましたが, A, B, C などの識別子は優先度がどの演算子よりも小さいと約束しておきます. これは括弧でくくることにより1つの式として表現された式についても同様です. したがって,明示的に括弧を使って,(A->B)->C と書けば,この二つの -> は どちらも xfy の型にあっていることになり,また,それ以外の解釈はあり得ません.
解釈しますね.
同じ優先度の :xfy と :yfx が同列に混ざった場合にはどうなるでしょう.
です.ここでは (A :xfy B) :yfx C の解釈にしました(と思います). 逆に,
となり,構文エラーです.
A---B は A - (-(-(B))) と解釈
下の例は,- の二項,一項の区別を字句解析のときに,識別子の 後ろには後置演算子あるいは二項演算子しか来ないことと,- は 後置演算子は無いことと,二項演算子項演算子の後ろには前置演算子しか こないことを使って前置演算子であることを決めています.
前置演算子には :fy だけでなく,:fx もあり得て,その場合は,その 演算子を複数続けてはいけないことになります.今回作った簡易パーサーでは こちらは今のところ実装していません.
のように構文解析できます.これも :xf という後置演算子があり得ますが,ここでは実装しませんでした.
DEC-10 Prolog には次の演算子もありますが,ここでは実装していません.
aandborcと表示されてしまいます.これは再度構文解析すると, きちんと元の構文解析結果に戻るのですが,人間にはどこで切れるか分からず, かなり読みにくいです. そこで,"and" と "or" の表示名をそれぞれ " and ", " or " にしておくと
a and b or cと表示されるという訳です.間に合わせの仕様で,あまり良くない仕様かも しれませんが,とりあえず,このようにしておきます.
英数字だけからなる演算子は両側に区切る文字あるいは行頭,行末が無い限り 演算子として切り出さないモードを作った.このモードがオンになっている ときは,aandb は a and b と区切られず,aandb という名前として認識される. 表示も自動的に a and b となるようにした.このモードは $sop_delimit_alpha_op と いう大域変数で制御する.
現時点では,ここで述べた表示名の機能はまだ有効である.
2019.02.27
次は
予め組み込まれている括弧の定義を次に示します.
$sop_ops = {
... #演算子の定義列
# paren =>
# [out_name, priority, paren_type, [pair_paren, ...], valOf(), marker
:"(" => ["(", 10000, :open, [:")"], "0", nil],
:")" => [")", 10000, :close, [:"("]],
:"[" => ["[", 10000, :open, [:"]"], [], :"#list#"],
:"]" => ["]", 10000, :close, [:"["]],
:"{" => ["{", 10000, :open, [:"}"], :"empty", :"#set#"],
:"}" => ["}", 10000, :close, [:"{"]],
括弧はこのように,
内部名 => [外部名, 優先度, 括弧の型, 対応括弧列, ()の値, マーカー
の形で定義されます.
それぞれを説明します.
[op, exp]を返します.
これも (,) の場合はあまり有難さを感じませんが,Ruby のリスト [a,b,c] の ような式を読みたい場合があります.掲載したプログラムリストの [] の定義では マーカーは :"#list#" となっていますから,[a, b, c,] を構文解析すると
[:"#list#", [",", "a", [",", "b", "c"]]]が返ります.このときの :fy 型の演算子も定義しなければならないことを 忘れないようにしてください.
ここで作成するのは演算子順位法によるパーサーですが,ここで応用例として挙げている 中で,λ計算の式は,演算子順位法によっては解析できません.これは
E1 E2のような構文があるためです.これは関数 E1 を E2 に適用することを表します. λ計算の理論ではこれを一々,apply(E1, E2) のように書きたくないので,単に E1 と E2 を並べて書きます.上の例では二つの式の間に空白がありますが, 明確に二つが分離できる場合は空白も書きません.例えば,(λx.x)(λx.x) など です.
この場合をうまく扱えるように,ここではこういう,式が並べて書いてあるところに 演算子を挿入していく方法をとります.これは最初に,入力を演算子や被演算子の列に 分解した後,式が二項演算子無しに隣り合っているところに,予め決めておいた 二項の演算子を挿入します.挿入される演算子は,Ruby の大域変数
$sop_implicit_opに入っている値とします.最初は,この変数には :"#apply#" が入っていますので,例えば,
(a b c)+1 は [:"+", [:"#apply#", "a", [:"#apply#", "b", "c"]], "1"]に解析されます.
λ計算やコンビネータ論理などの実験ではほとんど出てくることがありませんが, 時々,文字列を扱えたらよいと思うことがあります. それは非常に簡単な言語のインタープリタを作るときなどです.後に 挙げたプログラムでも,ごくごく簡単な文字列だけ最初から組み込んであります. これはユーザがカスタマイズすることができるものではありませんが, "..." は常に文字列として扱われて,構文解析後,「"」で始まって「"」で終わる文字列 として分離されています.ただし,... の部分は任意の文字列で,「"」を含ませたい 場合は,「\」でエスケープしてください.例えば,
"the symbol"+"* is star" は
[:"+", "\"the symbol\"", "\"* is star\""] として
この変数を true にすると,例えば,コンビネータなどの書き方を多くの教科書に 合わせるなどのことができます.例えば,S, K, I を使ったコンビネータの 教科書ではこれらを空白で区切らない書き方がされていることが多いです. そのような場合,"S", "K", "I" を それぞれ,:f 型の演算子として定義すれば,続けて書いた SKI コンビネータ式 SKI(KKS) などが S K I (K K S) のように分離されて入力されますので,コンビネータの 教科書などの式(空白が入っていないことが多い)を直接確かめることができます. 私は切って入力したほうが自分にあっているので,このモードは使いませんが.
内部処理は
def sop_parse(str, implicit_op_mode = true)
begin
sop_parse2(sop_split(str, implicit_op_mode))
rescue
:error
end
endのようになっていて,まず,sop_split() でトークン列に変換された 結果を,関数 sop_parse2() で構文木に変換する.その際,エラーが あれば,error というシンボル(:error)を返すようになっています.
この解説はまた時間ができたときにします.当面はじぶんで読んで下さい.
q と d 以外の入力は式の文字列が入力されている多として,それを構文解析した 結果が表示されます.表示は,解析結果の Ruby のデータそのものと,それを 演算子を考慮して表示したものです.後者は大部分の場合,入力と同じでしょう.
q を入力すると test を終わることができます. d はデバッグモードの ON/OFF を切り替えます.デバッグモードでは, まず,入力がどのようなトークン列に変換されたかを表示し,あとは, 入力を一つ読むごとの内部状態が表示され,どのように構文木が作られていくかの 過程が分かるようになっています.
$sop_ops[:"=>"] = ["=>", 1200, :xfy]のように入れることもできます. 関数 sop_parse() は呼ばれるたびに,内部で,この変数から動作のためのデータを 作り出しますから,データを変えれば,即,新しい定義が適用されます.
それに対して,$sop_implicit_op_mode が false や nil 以外なら, このような識別子と識別子の間などに暗黙の演算子が挟み込まれます. 暗黙の演算子はデフォルトでは :"#apply#" ですから,さきほどの a b は a #apply# b と書いてあるとみなされ,[:"#apply#", "a", "b"] という構文解析 結果が得られます.これは,コンビネータの解釈実行系を作るときなどに 便利です.例えば,
(S I I) は [:"#apply#", [:"#apply#", "S", "I"], "I"] と構文解析されます.
以上 2019年2月11日 Akihiko Koga
次の囲みの中のプログラムを選択してファイルとして セーブして,そのファイルを Ruby のインタープリタ(irb など)に 読み込んでください.私は sop.rb というファイル名を付けています. このプログラムの中にはテスト用の関数 test があります. 次の実行例で使い方が分かると思います.
こちらで使用した Ruby のバージョンは
ruby 2.3.3p222 (2016-11-21 revision 56859) [x64-mingw32]です.あまり高等な機能は使っていませんので,もう少し前のバージョンでも実行できると 思います.
プログラムは掲載リストをコピー&ペーストして使う形態をとりましたので,短くするために,コメントが殆どない, 少し詰まっている,トリッキーな書き方がしてあるなど,読みにくい部分があると 思います.プログラムの行数短縮を優先しましたのでご容赦ください. なお,変更履歴がこちらにあります.
# Simple Operator Precedence Parser
# by Akihiko Koga
# Version 1.02 2020.04.03
$sop_ops = {
# in_name => [out_name, priority, op_type]
:"->" => ["->", 1000, :xfy],
:"*" => ["*", 400, :yfx],
:"/" => ["/", 400, :yfx],
:"+" => ["+", 500, :yfx],
:"+/pre" => ["+", 200, :fy],
:"-" => ["-", 500, :yfx],
:"-/pre" => ["-", 200, :fy],
:"=" => ["=", 1500, :xfy],
:";/post" => [";", 1800, :yf],
:";" => [";", 1800, :yfx],
:"," => [",", 1400, :xfy],
:"#apply#" => ["#apply#", 1300, :yfx], # implicit operator
:"#list#" => ["#list#", 200, :fy], # list marker
:"#set#" => ["#set#", 200, :fy], # set marker
# paren =>
# [out_name, priority, paren_type, [pair_paren, ...], valOf(), marker
:"(" => ["(", 10000, :open, [:")"], "0", nil],
:")" => [")", 10000, :close, [:"("]],
:"[" => ["[", 10000, :open, [:"]"], [], :"#list#"],
:"]" => ["]", 10000, :close, [:"["]],
:"{" => ["{", 10000, :open, [:"}"], :"empty", :"#set#"],
:"}" => ["}", 10000, :close, [:"{"]],
}
$sop_follow = { # possible tokens that follow each token
:start => [:f, :fy, :open],
:open => [:f, :fy, :open, :close],
:close => [:yf, :yfx, :xfy, :close], # + $sop_follow2 if implicit_op_mode
:f => [:yf, :yfx, :xfy, :close], # same as above
:yf => [:yf, :yfx, :xfy, :close], # same as above
:fy => [:f, :fy, :open],
:xfy => [:f, :fy, :open],
:yfx => [:f, :fy, :open],
}
$sop_follow2 = $sop_follow.clone
[:close, :f, :yf].each {|x| $sop_follow2[x] += [:f, :fy, :open]}
$sop_implicit_op_mode = true
$sop_implicit_op = :"#apply#"
$sop_debug_mode = false
$sop_no_error_msg = false
$sop_delimit_alpha_op = false # e.g. "sort" => "s" "or" "t" if true
$sop_name_no = 0
$sop_print_limit = 1000
$sop_print_counter # counter to stop to print a very long expression
def sop_split(str, implicit_op_mode = $sop_implicit_op_mode)
# strings are replaced by temporary names first
ops, dic, prefix, i = {}, {}, "###", 0
str = str.gsub(/"([^"\\]|\\.)*"/) {|u|
tmp_name = prefix + i.to_s; i += 1
dic[tmp_name] = u
" " + tmp_name + " "
}
# gather out_names in $sop_ops and assign them temporary names seperated
# by space, split to tokens, rename temprary names to original names again
$sop_ops.sort{|a,b| b[1][0].length <=> a[1][0].length}.each {|op|
# op ::= [in_name, [out_name, ...]]
out_name = op[1][0]
if ops[out_name] == nil then
tmp_name = prefix + i.to_s; i += 1
dic[tmp_name] = out_name
ops[out_name] = []
if !$sop_delimit_alpha_op && out_name =~ /^(\w)+$/ then
pat = Regexp.new("([^\\w]|^)(" + out_name + ")([^\\w]|$)")
str = str.gsub(pat, '\1 \2 \3')
else
str = str.gsub(out_name, " " + tmp_name + " ")
end
end
ops[out_name].push(op)
}
tlist = str.split(" ").map {|x| if dic[x] then dic[x] else x end}
# decide op_type and replace out_name by in_name
tlist2, prev, n = [], :start, tlist.length
n.times{|i|
x = tlist[i]
oplist = ops[x] # ::= nil | [[in_name, [out_name, priority, op_type]], ...]
if oplist == nil then
in_name, type = x, :f
else
if i == n-1 then fols = [:close]
elsif ops[tlist[i+1]] == nil then fols = [:f]
else fols = ops[tlist[i+1]].map {|u| u[1][2]} end
op2 = sop_choose_op(oplist, prev, fols, $sop_follow)
if op2 == nil && implicit_op_mode then
op2 = sop_choose_op(oplist, prev, fols, $sop_follow2)
end
if op2 == nil then sop_error_at(tlist, i, "***SyntaxError1***") end
in_name, type = op2[0], op2[1][2]
end
if [:close, :yf, :f].index(prev) && [:open, :fy, :f].index(type) then
if implicit_op_mode then
tlist2.push($sop_implicit_op)
else
sop_error_at(tlist, i, "***BinaryOpRequiredBeforeThis***")
end
end
prev = type
tlist2.push(in_name)
}
tlist2
end
def sop_choose_op(oplist, prev, fols, follow)
oplist.find {|op| op_type = op[1][2]
follow[prev].index(op_type) && (follow[op_type] & fols) != [] }
end
# parser
def sop_parse(str, implicit_op_mode = $sop_implicit_op_mode)
sop_parse2([:"("] + sop_split(str, implicit_op_mode) + [:")"])
rescue
:error
end
def sop_parse2(tlist)
if $sop_debug_mode then printf("token_list= %s\n", tlist.to_s) end
arg_stack, op_stack = [], []
tlist.length.times{|i|
x = tlist[i]
if $sop_debug_mode then
printf("args: %s\nops: %s\ntoken: %s\n----\n", arg_stack, op_stack, x)
end
op_data = $sop_ops[x] # [in_name, priority, type, ...]
if op_data == nil || op_data[2] == :f then # identifier
arg_stack.unshift(x)
elsif op_data[2] == :open then # open parenthesis
arg_stack.unshift(x)
op_stack.unshift(x)
else # operator or close parenthesis
while x != nil && x != :error && sop_op_less(op_stack[0], x) do
arg_stack, op_stack, x = sop_reduce(arg_stack, op_stack, x)
end
if x == :error then
sop_error_at(tlist, i, "***SyntaxError2***")
elsif x != nil then
arg_stack.unshift(x)
op_stack.unshift(x)
end
end
}
if arg_stack.length != 1 then
sop_error_at(tlist, tlist.length-1, "***ExpNotCompleted***")
end
return arg_stack[0]
end
def sop_op_less(op1, op2)
p1, t1 = $sop_ops[op1][1], $sop_ops[op1][2]
p2, t2 = $sop_ops[op2][1], $sop_ops[op2][2]
return t2 == :close ||
(t2 != :open &&
((p1 < p2) || ((p1 == p2) && [:yf, :yfx].index(t2))))
end
def sop_error_at(tlist, i, msg)
if !$sop_no_error_msg then
p (i > 0?tlist[0..i-1]:[]) + [[msg, tlist[i]]] + tlist[i+1..-1]
end
raise msg
end
def sop_reduce(arg_stack, op_stack, op)
last_op = sop_shift(op_stack)
inf = $sop_ops[last_op] # [out_name, priority, op_type]
type = inf[2]
if type == :fy then
arg_stack[1] = [last_op, arg_stack[0]]
sop_shift(arg_stack);
elsif type == :yf then
arg_stack[1] = [last_op, arg_stack[1]]
sop_shift(arg_stack);
elsif type == :xfy || type == :yfx then # binary operator
arg_stack[2] = [last_op, arg_stack[2], arg_stack[0]]
sop_shift(arg_stack); sop_shift(arg_stack);
elsif type == :open && inf[3].index(op) then
# open paren and op is its close paren
if arg_stack[0] == last_op then # form of (), []
arg_stack[0] = inf[4]
else
arg_stack[1] = arg_stack[0]
sop_shift(arg_stack)
if inf[5] != nil then arg_stack[0] = [inf[5], arg_stack[0]] end
end
op = nil
else
return arg_stack, op_stack, :error
end
return arg_stack, op_stack, op
end
def sop_shift(x)
if x == [] then raise "***** shift of []" else x.shift end
end
def sop_delete_ops(ops)
if ops.class != Array then ops = [ops] end
dels = $sop_ops.to_a.select {|p| ops.index(p[1][0])}
dels.each {|p| $sop_ops.delete(p[0])}
end
def sop_print(code, nl = true, to_str = false)
$sop_print_counter = $sop_print_limit
if nl then r = sop_prin2(code) + "\n" else r = sop_prin2(code) end
if to_str then r else printf("%s", r) end
end
def sop_prin2(code, priority = 100000)
$sop_print_counter -= 1
if $sop_print_counter <= 0 then return "***** too long *****" end
if code.class != Array then code.to_s
elsif code == [] then "[]"
else
op = $sop_ops[code[0]] # [out_name, priority, op_type]
if op == nil then return code.to_s end
result = ""
if op[1] > priority then result += "(" end
if [:fy].index(op[2]) then
result += sop_op_string(code[0], op)
result += sop_prin2(code[1], op[1])
elsif [:yf].index(op[2]) then
result += sop_prin2(code[1], op[1])
result += sop_op_string(code[0], op)
elsif [:xfy, :yfx].index(op[2]) then
if op[2] == :xfy then d1,d2 = 1,0 else d1,d2 = 0,1 end
result += sop_prin2(code[1], op[1]-d1)
result += sop_op_string(code[0], op)
result += sop_prin2(code[2], op[1]-d2)
end
if op[1] > priority then result += ")" end
result
end
end
def sop_op_string(in_name, op)
if op[3] != nil then op[3]
elsif in_name == $sop_implicit_op then " "
else
out_name = op[0]
if !$sop_delimit_alpha_op && out_name =~/^(\w)+$/ then
if [:yf, :xfy, :yfx].index(op[2]) then out_name = " " + out_name end
if [:fy, :xfy, :yfx].index(op[2]) then out_name = out_name + " " end
end
out_name
end
end
def sop_print_tree2 (exp, col = 0, fp = $stdout, apply = "apply")
if exp == :"#apply#" then exp = apply end
if exp.class != Array then fp.printf("%s", exp.to_s); col + exp.to_s.length
else
len = exp.length
fp.printf("(");
col2 = sop_print_tree2(exp[0], col+1, fp, apply)
if (len > 1) then
fp.printf(" ")
start = true
(len-1).times {|i|
x = exp[i+1]
if !start then fp.printf("\n"); (col2+1).times { fp.printf(" ")} end
start = false
sop_print_tree2(x, col2+1, fp, apply)
}
end
fp.printf(")")
end
end
def sop_gen_toggle(vname, msg = nil, vals = [true, false])
if msg == nil then msg = " " + vname + " = " end
lambda {|input, code|
i = vals.index(eval(vname))
if i == nil then v2 = vals[0] else v2 = vals[(i + 1) % vals.length] end
eval(sprintf("%s = %p", vname, v2))
printf("%s%p\n", msg, v2)
}
end
$sop_basic_commands = {":q" => lambda {|input, code| $sop_top_end = true}}
def sop_new_commands(commands, parent = $sop_basic_commands)
x = parent.clone.update(commands)
if x[":help"] == nil then
x[":help"] = lambda {|input, code|
clist = x.keys.map {|k| if $sop_ops[k] then $sop_ops[k][0] else k end}
printf("Commands are:\n %s\n", (clist-[:else]).join(", "))}
end
x
end
def sop_top(opening, ending, prompt, commands, pre = nil, post = nil, p0 = nil)
printf("%s", opening)
$sop_top_last_input, $sop_top_last_code = "", ""
$sop_top_end = false; $sop_exception = nil
while !$sop_top_end do
printf("%s", prompt)
$sop_top_input = readline.strip
if p0 != nil then $sop_top_input = p0.call($sop_top_input) end
$sop_top_code = sop_parse($sop_top_input)
if pre != nil then pre.call($sop_top_input, $sop_top_code) end
sop_interpret($sop_top_input, $sop_top_code, commands)
if post != nil then post.call($sop_top_input, $sop_top_code) end
end
printf("%s", ending)
end
def sop_interpret(line, code, commands)
if commands[code] then
commands[code].call(line, code)
elsif code.class == Array && commands[code[0]] then
commands[code[0]].call(line, code)
elsif commands[:else] then
commands[:else].call(line, code)
end
rescue => $sop_exception
printf("***** Evaluation error:\n %s\n", $sop_exception.message)
end
def sop_load(file, commands, p0 = nil)
fp = nil
fp = open(file, "r")
fp.each {|line|
$sop_load_line = line.strip
if p0 != nil then $sop_load_line = p0.call($sop_load_line) end
if $sop_load_line != "" then
sop_interpret($sop_load_line, sop_parse($sop_load_line), commands)
end
}
printf("File %s loaded\n", file)
fp.close
rescue => $sop_exception
if fp == nil then printf("***** %s cannot open\n", file)
else
printf("***** System Error \"%s\" \n at \"%s\" \n in \"%s\"\n",
$sop_exception.to_s, $sop_load_line, file)
fp.close
end
end
def sop_new_name(prefix = "sop", no = nil)
if no != nil then $sop_name_no = no end
name = sprintf("%s%04d", prefix, $sop_name_no)
$sop_name_no += 1
name
end
$sop_top_opening = "Welcome to SopTest\n :q for quit\n :d for toggling debug mode
:i for toggling implicit op mode\n Otherwise, parsed and printed\n"
$sop_top_commands = sop_new_commands ({
":d" => sop_gen_toggle("$sop_debug_mode"),
":i" => sop_gen_toggle("$sop_implicit_op_mode"),
:else => lambda {|input, code|
printf(" %s\n", code.to_s)
printf(" print-form = "); sop_print(code)
printf(" "); sop_print_tree2(code, 2); printf("\n")},
})
def test
sop_top($sop_top_opening, "Bye\n", "input> ", $sop_top_commands)
end
次の実行例は,上のプログラムを"sop.rb" という名前をファイルにセーブして 実行したものです.test という関数が入っているので,これを動かすと, すでに定義されている演算子で何が解析できるかを確認できます.
test はコマンドとして,
:q ... test から抜ける
:i ... 暗黙の演算子モードのON/OFFを切り替える.最初は ON
:d ... デバッグモードの ON/OFFを切り替える.ON だと,構文解析の
様子が多少表示される.最初は OFF
の3つだけを持ち,他の入力は式として構文解析され,その結果が表示されます.
c:\0-ruby\sop>irb
irb(main):001:0> load "sop.rb"
=> true
irb(main):006:0> test
Welcome to SopTest
:q for quit
:d for toggling debug mode
:i for toggling implicit op mode
Otherwise, parsed and printed
コマンドとしては :q, :d, :i が可能で,ほかは全部構文解析されて結果が表示されます.
input> a*b-c/d
[:-, [:*, "a", "b"], [:/, "c", "d"]]
print-form = a*b-c/d
(- (* a
b)
(/ c
d))
a*b-c/d の構文解析の結果とそれを式として表示したところです.構文解析結果の先頭の :- は,単に - というシンボルで,:"-" と一緒です.Ruby のプリントはRubyの表示上問題ないときは"を付けないみたいですね.
最後の表示は構文木の構造を簡易に表示したものです.直接に構文木をみるより
見やすいと思います.
input> A->B->C->D
[:"->", "A", [:"->", "B", [:"->", "C", "D"]]]
print-form = A->B->C->D
(-> A
(-> B
(-> C
D)))
input> A->(B->C)->D
[:"->", "A", [:"->", [:"->", "B", "C"], "D"]]
print-form = A->(B->C)->D
(-> A
(-> (-> B
C)
D))
演算子 -> は :xfy の二項演算子として定義されていますので,何も括弧を指定しないと右側から括弧がついて構文解釈されますが,明示的に括弧を使うと,そこが先に構文解析されます.
input> (f x y) + (g x)
[:+, [:"#apply#", [:"#apply#", "f", "x"], "y"], [:"#apply#", "g", "x"]]
print-form = (f x y)+(g x)
(+ (apply (apply f
x)
y)
(apply g
x))
これは暗黙の演算子の例です.(f x y) は演算子で結ばれていないので,演算子文法としては間違った書き方なのですが, f と x の間と x と y の間に関数適用の演算子 "#apply#" があるとみなして構文解析します."#apply#" は :yfx の演算子として定義していますので,f を x に適用した結果の (f x) が何らかの関数と見て,それを y に適用するという意味の構文解析結果になっています.簡易構文木の中では #apply# はちょっとうるさい感じがしたので apply と表示してあります.
input> :i
implicit op mode = false
暗黙の演算子モードを解除しました(:i ごとに ON/OFF が切り替わる).
input> (f x y)+(g x)
["(", "f", ["***BinaryOpRequiredBeforeThis***", "x"], "y", ")", "+", "(", "g", "x", ")"]
error
print-form = error
error
直前に構文解析できていた式が構文エラーになります.エラーメッセージはあまり親切ではありません.
input> :d
debug mode = true
デバッグモードをONにしました.こちらも ON/OFF の切り替えです.以下,最初に,入力がどのようなトークン列に分解されたかが示され,その後は1トークンごとの解析過程が示されます.入力の終わりや閉じ括弧はかなり沢山の還元(reduction)が行われるため,もしかしたらソースプログラムに手を入れて,もう少し詳細に見せても良いかもしれません.
input> a*b+c*d
token_list= [:"(", "a", :*, "b", :+, "c", :*, "d", :")"]
args: []
ops: []
token: (
----
args: [:"("]
ops: [:"("]
token: a
----
args: ["a", :"("]
ops: [:"("]
token: *
----
args: [:*, "a", :"("]
ops: [:*, :"("]
token: b
----
args: ["b", :*, "a", :"("]
ops: [:*, :"("]
token: +
次のトークンが「+」で」一つ前のトークン「*」より優先度が低いので次で「*」の方がまとめられます.
----
args: [:+, [:*, "a", "b"], :"("]
ops: [:+, :"("]
token: c
はい,まとめられました.
----
args: ["c", :+, [:*, "a", "b"], :"("]
ops: [:+, :"("]
token: *
----
args: [:*, "c", :+, [:*, "a", "b"], :"("]
ops: [:*, :+, :"("]
token: d
----
args: ["d", :*, "c", :+, [:*, "a", "b"], :"("]
ops: [:*, :+, :"("]
token: )
入力がすべて終わった(次のトークンがすべての式を閉じる「)」)なのですべての演算子がまとめられます.
----
[:+, [:*, "a", "b"], [:*, "c", "d"]]
print-form = a*b+c*d
(+ (* a
b)
(* c
d))
次は暗黙の演算子モードに戻して,デバッグモードで実行してみます
input> :i
implicit op mode = true
input> f x+y
token_list= [:"(", "f", :"#apply#", "x", :+, "y", :")"]
は,"#aply#" が入力に挿入されていることがわかりますね.
args: []
ops: []
token: (
----
args: [:"("]
ops: [:"("]
token: f
----
args: ["f", :"("]
ops: [:"("]
token: #apply#
----
args: [:"#apply#", "f", :"("]
ops: [:"#apply#", :"("]
token: x
----
args: ["x", :"#apply#", "f", :"("]
ops: [:"#apply#", :"("]
token: +
----
args: [:+, "x", :"#apply#", "f", :"("]
ops: [:+, :"#apply#", :"("]
token: y
----
args: ["y", :+, "x", :"#apply#", "f", :"("]
ops: [:+, :"#apply#", :"("]
token: )
----
[:"#apply#", "f", [:+, "x", "y"]]
print-form = f x+y
(apply f
(+ x
y))
input> :d
debug mode = false
次はリストの解析例を示してこの実行例を終わります.
input> [a,b,c]
[:"#list#", [:",", "a", [:",", "b", "c"]]]
print-form = #list#(a,b,c)
(#list# (, a
(, b
c)))
input> [a, b+1, a->c*d]
[:"#list#", [:",", "a", [:",", [:+, "b", "1"], [:"->", "a", [:*, "c", "d"]]]]]
print-form = #list#(a,b+1,a->c*d)
(#list# (, a
(, (+ b
1)
(-> a
(* c
d)))))
input> :q
=> nil
irb(main):007:0>
上が最近です.
英数字だけからなる演算子は両側にデリミターかテキストの最初,最後が 無い限り演算子として切り出さないモードを実装し,こちらをデフォルトとした. このモードは $sop_delimit_alpha_op で制御する.$sop_delimit_alpha_op が true のときは,英数字の列の中に演算子があっても切り出す.例えば,or が演算子なら, sort は s or t のように分解される.この大域変数が false のときは sort という 名前と認識される.汎用のトップループ関数 sop_top(...) に簡易ヘルプ機能を付けた.
あと,某筋の情報によると,中田先生の本では,次の本が評判が良いらしいです.
その他にも構文解析やコンパイラの本は世の中に沢山ありますから,探して 自分に合いそうな本を見つけてください.私の本だなや近くの図書館には, 演算子順位法の載っている本(で,かつ,今でも絶版になってない本 :-))としては, 次の本がありました.
本格的なコンパイラを 作る手法としては主流ではありませんので,中には省略している本もあります. このページでは構文解析やコンパイラ作成がメインの目的ではなく,ちょっとした 言語を簡単に導入して,計算機科学の実験をすることがメインの目的なので 演算子順位法を使いました.
計算機(主にソフトウェア)の話題 へ
圏論を勉強しよう へ
束論を勉強しよう へ
半群論を勉強しよう へ
ホームページトップ(Top of My Homepage)