計算機(主にソフトウェア)の話題
(Topics about Computer (mainly Software))
by Akihiko Koga
30th Mar. 2021 (Update)
14th July 2018 (First)
ここでは,計算機,主にソフトウェアのことについて,考えたこと,思いついたこと,
徒然思い続けていることを書くつもりです.どちらかと言えば,数学より計算機よりの話題,
例えば,アルゴリズムやプログラミング,ちょっと理論よりではプログラム変換などの
お話です.たぶん,圏論や束論はあまり出ないし,出てきても主役ではないと思います.
話題
- 線形オーダーのハノイの塔のプログラム 2018.07.14 (土)
 ハノイの塔のプログラムは再帰関数を説明するときよく使われる例題ですが,
通常, n 枚の円盤を動かすのに 2n - 1 の手順が必要ですから,
それを生成するのに O(2n)の計算量が必要です.ここでは,
結果を表示せず,データとして計算だけすることにして O(n) のオーダーで
計算を終わらせようというものです.内容を読んだら,多少,ずるいと思うかも
しれませんし,これは違うと思うかもしれません.
ハノイの塔のプログラムは再帰関数を説明するときよく使われる例題ですが,
通常, n 枚の円盤を動かすのに 2n - 1 の手順が必要ですから,
それを生成するのに O(2n)の計算量が必要です.ここでは,
結果を表示せず,データとして計算だけすることにして O(n) のオーダーで
計算を終わらせようというものです.内容を読んだら,多少,ずるいと思うかも
しれませんし,これは違うと思うかもしれません.
- コンビネータ論理(Combinatory Logic) のお話
: λ式から SKI を使った式への変換のトレース 2018.07.20 (金)
 一か月ほど前に,とある勉強会でコンビネータ論理を勉強してきた.勉強会に
参加する前に,予習として事前にWikipedia などを見て,SKI コンビネータの式のインタープリタと
λ式から SKI コンビネータの式へ変換するツールを Ruby で書いてみた.
そのツールには変換のトレース機能があり,変換の過程が分かって,結構良いのではないかと思うので,それを動かしながら,
λ式から SKI コンビネータの式への変換方法を解説してみた.
一か月ほど前に,とある勉強会でコンビネータ論理を勉強してきた.勉強会に
参加する前に,予習として事前にWikipedia などを見て,SKI コンビネータの式のインタープリタと
λ式から SKI コンビネータの式へ変換するツールを Ruby で書いてみた.
そのツールには変換のトレース機能があり,変換の過程が分かって,結構良いのではないかと思うので,それを動かしながら,
λ式から SKI コンビネータの式への変換方法を解説してみた.
- ドメイン取得とレンタルサーバーのお話
2018.11.04 (日)
 このコンテンツを置いていた geocities.jp からサイトを閉鎖すると連絡が
ありましたので,独自ドメイン取得とレンタルサーバーを借りることに
なってしまいました.そのとき検討したことを残しておこうという内容です.
今までの少し理論っぽい話とはだいぶ趣が違いますね.
このコンテンツを置いていた geocities.jp からサイトを閉鎖すると連絡が
ありましたので,独自ドメイン取得とレンタルサーバーを借りることに
なってしまいました.そのとき検討したことを残しておこうという内容です.
今までの少し理論っぽい話とはだいぶ趣が違いますね.
- 簡単な演算子順位パーサー in Ruby を作る
2019.02.11 (月)
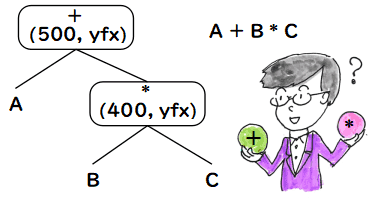 λ計算やコンビネータ論理,あるいは,それらをベースに型理論を導入したり,あるいは
圏論を利用してそれらのモデルを作ったりと,計算機科学も数学と同様に抽象的で
難しい領域があります.そんなとき,計算機屋さんの良いところは,ちょっと作って
動かしてみることではないでしょうか.Ruby や LISP なら比較的簡単に原理実験的に
動くものができます.ただし,「簡単に」というのは見た目にこだわらず,それらの
言語のリストや配列を直接人間が扱う場合です.やはり,そういうのでは数学を
やっているという雰囲気が出ないので,数式や何らかの人間に優しい言語でそれらの
実験ができれば助かります.ここは,本当に簡単なパーサーを作っておいて,
計算機科学の理論の勉強に役立てようという企画です.まずは作るだけで,
使うのは今後になると思います.
λ計算やコンビネータ論理,あるいは,それらをベースに型理論を導入したり,あるいは
圏論を利用してそれらのモデルを作ったりと,計算機科学も数学と同様に抽象的で
難しい領域があります.そんなとき,計算機屋さんの良いところは,ちょっと作って
動かしてみることではないでしょうか.Ruby や LISP なら比較的簡単に原理実験的に
動くものができます.ただし,「簡単に」というのは見た目にこだわらず,それらの
言語のリストや配列を直接人間が扱う場合です.やはり,そういうのでは数学を
やっているという雰囲気が出ないので,数式や何らかの人間に優しい言語でそれらの
実験ができれば助かります.ここは,本当に簡単なパーサーを作っておいて,
計算機科学の理論の勉強に役立てようという企画です.まずは作るだけで,
使うのは今後になると思います.
- SKIコンビネータ AGAIN 2019.02.11 (月)
 上で作成した演算子順位法のパーサーを使って,SKI コンビネータのインタープリタを
作成し,遊ぼうという企画です.SKIコンビネータの話は上にもありますが,
そちらでは動くものは提供しませんでした.すぐ上で,パーサーの小さなものが
できたので,それを使って,それぞれが玩具程度のちいさなプログラムで遊べるようになりました,
こちらは動かして遊ぶということがメインなので,コンビネータの説明は
上の「コンビネータ論理(Combinatory Logic) のお話 : λ式から SKI を使った式への変換のトレース」の方をあわせて読んでいただくと良いと思います.
上で作成した演算子順位法のパーサーを使って,SKI コンビネータのインタープリタを
作成し,遊ぼうという企画です.SKIコンビネータの話は上にもありますが,
そちらでは動くものは提供しませんでした.すぐ上で,パーサーの小さなものが
できたので,それを使って,それぞれが玩具程度のちいさなプログラムで遊べるようになりました,
こちらは動かして遊ぶということがメインなので,コンビネータの説明は
上の「コンビネータ論理(Combinatory Logic) のお話 : λ式から SKI を使った式への変換のトレース」の方をあわせて読んでいただくと良いと思います.
- 動かして遊ぶλ計算の初歩 in Ruby 2019.02.21 (木)
 上で作成した演算子順位法のパーサーを使って,ラムダ計算のインタープリタを
作成し,遊ぼうという企画です.これは型無しのλ計算の話題で,理論に深入りするというよりは,これで計算ができるということを実感することを目的としています.今後,λ計算の
理論,型ありλ計算,λ計算の意味論など計算機科学を学習するにあたって,λ計算が身近に感じられると,少しは学習の障壁が低くなるのではないかと思って企画しました.尚,上ですでに
挙げている,「コンビネータ論理(Combinatory Logic) のお話 : λ式から SKI を使った式への変換のトレース」と「SKIコンビネータ AGAIN」を合わせて読むと,相乗効果があると思います.
特に後者も動かして遊ぶ企画ですので,計算を身近に感じるということに効果があります.
上で作成した演算子順位法のパーサーを使って,ラムダ計算のインタープリタを
作成し,遊ぼうという企画です.これは型無しのλ計算の話題で,理論に深入りするというよりは,これで計算ができるということを実感することを目的としています.今後,λ計算の
理論,型ありλ計算,λ計算の意味論など計算機科学を学習するにあたって,λ計算が身近に感じられると,少しは学習の障壁が低くなるのではないかと思って企画しました.尚,上ですでに
挙げている,「コンビネータ論理(Combinatory Logic) のお話 : λ式から SKI を使った式への変換のトレース」と「SKIコンビネータ AGAIN」を合わせて読むと,相乗効果があると思います.
特に後者も動かして遊ぶ企画ですので,計算を身近に感じるということに効果があります.
- Forth-like な言語を作ってみたことによる考察 2019.04.10 (水)
 Forth に似たプログラミング言語を作って遊んでみました.Forth は
スタック操作を原理とする,とても小さな,そして興味深い言語です.
本当は,今回は
上のパーサ活用シリーズで,命題論理の勉強をするはずだったのですが,
結構考えることが多くてまとまらないうちに,なぜか
小さなプログラミング言語の方に活動が移ってしまいました.
しかし上でコンビネータ論理,λ計算とやってきて,次が計算機の
モデルに関係が深いトピックスなので,
結果的に「計算とは何か?」を考えるための良い順序になっているような
気もします.「命題論理で遊ぶ」のはまた今度ということで,まずは,
計算についてちょっと考えてみましょう.
Forth に似たプログラミング言語を作って遊んでみました.Forth は
スタック操作を原理とする,とても小さな,そして興味深い言語です.
本当は,今回は
上のパーサ活用シリーズで,命題論理の勉強をするはずだったのですが,
結構考えることが多くてまとまらないうちに,なぜか
小さなプログラミング言語の方に活動が移ってしまいました.
しかし上でコンビネータ論理,λ計算とやってきて,次が計算機の
モデルに関係が深いトピックスなので,
結果的に「計算とは何か?」を考えるための良い順序になっているような
気もします.「命題論理で遊ぶ」のはまた今度ということで,まずは,
計算についてちょっと考えてみましょう.
P.S. できるだけ小さい言語処理系を書いてみるという裏の野望もあるので,
「ここに何行必要になる」というようなセコイ話になっている部分もあります.
- ガロア接続に基づく形式的概念分析の実験プログラム 2021.03.30 (火)
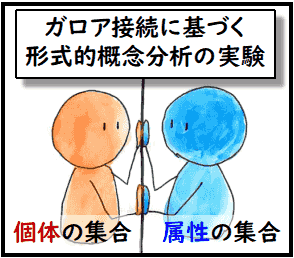 ガロア接続の応用に形式的概念分析(Formal Concept Analysis)
というものがあります.これは,色々な個体が
色々な属性を持っている状況で,
属性の集合と,それらの属性の集合を満たす個体の集合同士を結び付けて「概念」
を
形成するという応用です.最近,順序集合のお勉強のページで,
順序集合や束などに関する基本的な概念の説明を大幅に更新して,
ガロア接続や形式的概念分析の説明を書きました.そのとき,
形式的概念分析の原理実験用の Ruby プログラムを作成しましたので,
ここではそのプログラムについて書きました.データ分を除くと 70行
位のごく短いプログラムです.
ガロア接続の応用に形式的概念分析(Formal Concept Analysis)
というものがあります.これは,色々な個体が
色々な属性を持っている状況で,
属性の集合と,それらの属性の集合を満たす個体の集合同士を結び付けて「概念」
を
形成するという応用です.最近,順序集合のお勉強のページで,
順序集合や束などに関する基本的な概念の説明を大幅に更新して,
ガロア接続や形式的概念分析の説明を書きました.そのとき,
形式的概念分析の原理実験用の Ruby プログラムを作成しましたので,
ここではそのプログラムについて書きました.データ分を除くと 70行
位のごく短いプログラムです.
圏論を勉強しよう へ
束論を勉強しよう へ
半群論を勉強しよう へ
ホームページトップ(Top of My Homepage)
 ハノイの塔のプログラムは再帰関数を説明するときよく使われる例題ですが,
通常, n 枚の円盤を動かすのに 2n - 1 の手順が必要ですから,
それを生成するのに O(2n)の計算量が必要です.ここでは,
結果を表示せず,データとして計算だけすることにして
ハノイの塔のプログラムは再帰関数を説明するときよく使われる例題ですが,
通常, n 枚の円盤を動かすのに 2n - 1 の手順が必要ですから,
それを生成するのに O(2n)の計算量が必要です.ここでは,
結果を表示せず,データとして計算だけすることにして  一か月ほど前に,とある勉強会でコンビネータ論理を勉強してきた.勉強会に
参加する前に,予習として事前にWikipedia などを見て,SKI コンビネータの式のインタープリタと
一か月ほど前に,とある勉強会でコンビネータ論理を勉強してきた.勉強会に
参加する前に,予習として事前にWikipedia などを見て,SKI コンビネータの式のインタープリタと
 このコンテンツを置いていた geocities.jp からサイトを閉鎖すると連絡が
ありましたので,
このコンテンツを置いていた geocities.jp からサイトを閉鎖すると連絡が
ありましたので,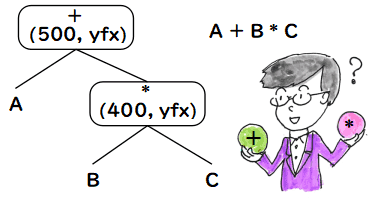 λ計算やコンビネータ論理,あるいは,それらをベースに型理論を導入したり,あるいは
圏論を利用してそれらのモデルを作ったりと,計算機科学も数学と同様に抽象的で
難しい領域があります.そんなとき,計算機屋さんの良いところは,ちょっと作って
動かしてみることではないでしょうか.Ruby や LISP なら比較的簡単に原理実験的に
動くものができます.ただし,「簡単に」というのは見た目にこだわらず,それらの
言語のリストや配列を直接人間が扱う場合です.やはり,そういうのでは数学を
やっているという雰囲気が出ないので,数式や何らかの人間に優しい言語でそれらの
実験ができれば助かります.ここは,
λ計算やコンビネータ論理,あるいは,それらをベースに型理論を導入したり,あるいは
圏論を利用してそれらのモデルを作ったりと,計算機科学も数学と同様に抽象的で
難しい領域があります.そんなとき,計算機屋さんの良いところは,ちょっと作って
動かしてみることではないでしょうか.Ruby や LISP なら比較的簡単に原理実験的に
動くものができます.ただし,「簡単に」というのは見た目にこだわらず,それらの
言語のリストや配列を直接人間が扱う場合です.やはり,そういうのでは数学を
やっているという雰囲気が出ないので,数式や何らかの人間に優しい言語でそれらの
実験ができれば助かります.ここは, 上で作成した演算子順位法のパーサーを使って,
上で作成した演算子順位法のパーサーを使って, 上で作成した演算子順位法のパーサーを使って,
上で作成した演算子順位法のパーサーを使って, Forth に似たプログラミング言語を作って遊んでみました.
Forth に似たプログラミング言語を作って遊んでみました.