(Hanoi's Tower Program in Linear Order)
ハノイの塔の解は 2n 手順からなるので,全部表示していては それだけで O(2n) かかる.したがって,ここでは手順をデータとして 求めるだけで,それを表示するところは切り離して考える.以下の答えを見ると, それでもずるいと 思う人もいるかもしれないし,これは最終的な解と呼べないんじゃないかと 思う人もいるかもしれない.考え出すと,「計算って何だろう?」という問いに 向かい合うような問題である.
なお,この方法は 34年前 (1984年) に修士論文でプログラム変換を考えていた時, できるはずだと思いつつ,面倒なので放っておいたもので,会社をやめて昨年 やってみたらあっさりできたというものである(正確には,「出来たと思うことにした.」 と言うのが正しいような気がする.解の手順を一次元に繋ぐのを諦めただけなので).
それを1枚ずつ動かして全部を場所 B に移す問題である.ただし, 円盤は大きさが皆異なり,大きな円盤を小さな円盤の上に置いてはいけないという 制約がある.この制約を守りつつ,3つの場所を上手く使って全部を場所 B に持っていく という問題である.
この問題は,まず n-1 個の円盤をなんとかして場所 C に持って行って,おもむろに,一番大きな 円盤を場所 A から場所 B に移動し,そして待避していた場所 C の n-1 枚の円盤を 場所 C から,場所 B に写せばよい.例えば, Ruby で書くと,次のようになる.
defhanoi(n, a, b, c) if (n == 0) # do nothing elsehanoi(n-1, a, c, b) printf("Move disk %d from %s to %s\n", n, a, b)hanoi(n-1, c, b, a) end end hanoi(3, "A", "B", "C")
このように呼び出すと次のような解を表示してくれる.再帰定義とは,本当に便利な機能である.
Move disk 1 from A to B Move disk 2 from A to C Move disk 1 from B to C Move disk 3 from A to B Move disk 1 from C to A Move disk 2 from C to B Move disk 1 from A to B
この定義だと人間には見やすいが,printf() という副作用が ある関数を使っているので,次のように,解をリストとして返すように 書き換えておこう.また,再帰呼び出しの回数を数えるために大域変数 $count1 を 使っている.
defhanoi(n, a, b, c) $count1 = 0hanoi1(n, a, b, c) end defhanoi1(n, a, b, c) $count1 += 1 if (n == 0) [] elsehanoi1(n-1, a, c, b) + ["Move disk " + n.to_s + " from " + a + " to " + b] +hanoi1(n-1, c, b, a) end end hanoi(3, "A", "B", "C")
結果は次のようになる.
["Move disk 1 from A to B", "Move disk 2 from A to C", "Move disk 1 from B to C", "Move disk 3 from A to B", "Move disk 1 from C to A", "Move disk 2 from C to B", "Move disk 1 from A to B"]
また,再帰呼び出しの回数 $count1 は 15 になる.
このプログラムの計算量は関数 hanoi() が呼び出される回数 C(n) を指標にとると,
C(0) = 1 C(n+1) = 2*C(n) + 1 故に C(n) = 2n+1 - 1と,O(2n) になる.
以下で,関数の再帰呼び出しのオーダーを O(n) に変えるのだが,実は,配列の
結合 [...] + [...] は前の配列の長さに比例するので,関数呼び出しだけを
少なくしても,計算量はあまり変わらないということになる.
defhanoi2(n, a, b, c) $memo = {} # 計算結果を記憶しておくデータとして連想記憶を使う $count2 = 0hanoi2b(n, a, b, c) end defhanoi2b(n, a, b, c) $count2 += 1 result = $memo[[n, a, b, c]] if result != nil then return result end if (n == 0) result = [] else result =hanoi2b(n-1, a, c, b) + ["Move disk " + n.to_s + " from " + a + " to " + b] +hanoi2b(n-1, c, b, a) end $memo[[n, a, b, c]] = result result end # 結果を表示してしまうと時間がかかるので呼び出しは次のようにする. xxx=hanoi2(10, "A", "B", "C") ; nil $count2 # hanoi2() の呼び出し回数は 55 xxx.length # 解の長さは 1023 # 2**10 - 1 = 1023 なので確かに答えがでているみたい xxx==hanoi(10, "A", "B", "C") true # 確かに答えはあってます
この例題では hanoi2() の呼び出し回数は, n=10 のとき 55 になっている. 以前のプログラムでは 211-1=2047 回のはずなので これで多少は関数呼び出しの負荷は減るが,依然として配列を結合する 負荷が高いのと,結果が大きいので,私の計算機では n が 20 を過ぎた あたりから急速に遅くなり,n = 30 は計算できなかった,というか,途中で止めた. なんせ, n=30 の ときは解の長さが 230 - 1 = 1,073,741,823 なので, ちょっと辛い.スワッピングが起こって大変なのであまり大きな n で やらないようにしておいたほうが良い.私は,退職して収入が無くなったので 計算機の買い替えはできるだけ控えたいという事情があるのだ.
これをさらに実際にリニアオーダーで動作するプログラムに改良する方に 興味がある方は,ここからすぐに次の章の4. 配列の結合の効率化に 進んで構わない.しかし,私としてはプログラム変換に興味があるので, ついででもよいので後で,「3.2 タプリング戦略を使ったハノイの塔のプログラムの改善」も少しだけ覗いていただけると嬉しい.
最初から説明すると時間がかかるので,ここは天下り式に次のような 関数
hanoi_triple(n, a, b, c)
を考えてみる.(注意1)
def hanoi_triple(n, a, b, c)
[hanoi(n, a, b, c), hanoi(n, b, c, a), hanoi(n, c, a, b)]
end
このように定義すると, hanoi_triple(n-1, a, c, b) は
を計算することになる.実は,これらの式が計算されているとすると,上の元々の3つ組,(*) [hanoi(n-1, a, c, b), hanoi(n-1, c, b, a), hanoi(n-1, b, a, c)]
は計算できるのである.例えば,(**) の1番目は,(*) の1番目と2番目によって 達成できることは最初のハノイのプログラムの再帰定義から明らかだから,真ん中の hanoi(n, b, c, a) を確かめてみる.(**) [hanoi(n, a, b, c), hanoi(n, b, c, a), hanoi(n, c, a, b)]
によって達成できる.(**) の3番目は自分で確かめて欲しい.hanoi(n, b, c, a) (つまり,n 個の円盤を b から c に移動する)のは 円盤 n-1 個を b から a に移動して ((*) の3番目 hanoi(n-1, b, a, c)), 円盤 n を b から c に直接移動して, 円盤 n-1 個を a から c に移動する ((*) の1番目 hanoi(n-1, a, c, b))
このような関係を見抜けば,hanoi_triple() を次のように自分を1回だけ再帰呼び出し する形に書き直すことができる.
# 次のプログラムの中で hanoi_triple(n, a, b, c) は, # [hanoi(n, a, b, c), hanoi(n, b, c, a), hanoi(n, c, a, b)] # を計算することを意図した関数である defhanoi3(n, a, b, c) $count3 = 0hanoi_triple(n, a, b, c) [0] end defhanoi_triple(n, a, b, c) $count3 += 1 if n == 0 then [[], [], []] else x =hanoi_triple(n-1, a, c, b) [x[0] + ["Move disk " + n.to_s + " from " + a + " to " + b] + x[1], x[2] + ["Move disk " + n.to_s + " from " + b + " to " + c] + x[0], x[1] + ["Move disk " + n.to_s + " from " + c + " to " + a] + x[2]] end end yyy=hanoi3(10, "A", "B", "C") ; nil $count3 # 再帰呼び出しは 11 回 11 yyy==hanoi(10, "A", "B", "C") true # 答えはあってます
このような補助的な関数を系統的に見つける方法を私は 1983年-1984年位の時期に修士論文の テーマとして考えていた. 一応,論文として出した(参考文献)のだが,煩雑なことと, タイポも沢山あって読みにくかったせいか,だれも読んでくれていないように思う. 時間ができたら,単純化してここで解説してみたいと思う.ただし,ハノイの塔がこのようにリニアな呼び出しだけで書けるということ 自身は,それより以前に Alberto Pettorossi 氏などが論文としてすでに出していた. 私が取り組んだのは,このような補助的な関数の系統的な導入方法である. プログラム変換は劇的な効率改善ができることがあるのだが,補助的な関数を 考え出すという人間のインテリジェンスを要求する.そこを少しでも自動化, あるいは,系統的な手法でできるようにしたかったのである.
配列やリストの表現方法にはいろいろな方法がある.例えば,昔,論理型言語の Prolog には 差分リストというものがあった.リスト2つ X と Y を用意して,X から Y を引いたものを 表しているとするものだ.実際は,X と Y は一つのリストの2か所を保持していて, Y のところに何か追加して,Y をその後ろにずらすことで,後ろに簡単に要素がつけられる など,リスト操作のいくつかが効率的にできるようになっている.
それにならって,計算結果の配列が必ずしも,意図するものの直接の配列表現になって いなくても,意図するものとしての解釈ができれば良いのではないかと考えてみた. ハノイの問題の解の中には多くの同一の移動列が複数回出現する.それらを共有して リンク構造だけで全体を表現する方法があれば,配列の結合も,解の移動列が占める メモリーももっと効率よくできるのではないだろうかという訳である.
結果から言うと,移動列の断片自身に次につながるリンクを持たせるのではできない. 同じ移動列が複数のコンテキストで使われている可能性があるからである.
そこで,例えば次のような約束事を決めてみたらどうだろう?

つまり,*expand* で始まる配列が要素部分にあれば,そこにそれを展開した
配列を表しているとみるのである.これをこのまま実装してみてもよいのだが
ここで作成しているハノイの塔の場合は,移動操作は文字列で表しているので
[X1, X2, [Y1, Y2, Y3], X3, X4]
と書いてあったら
[X1, X2, Y1, Y2, Y3, X3, X4]
と書いてあると思えということである).
そうするとメモ化のプログラムは次のようになる.
defhanoi2(n, a, b, c) $memo = {} # 計算結果を記憶しておくデータとして連想記憶を使う $count2 = 0hanoi2b(n, a, b, c) end defhanoi2b(n, a, b, c) $count2 += 1 result = $memo[[n, a, b, c]] if result != nil then return result end if (n == 0) result = [] else # 要は次の部分の配列の連結をやめて 3 つの要素のリストにしただけ result = [hanoi2b(n-1, a, c, b) , "Move disk " + n.to_s + " from " + a + " to " + b,hanoi2b(n-1, c, b, a) ] end $memo[[n, a, b, c]] = result result end # 次の結果は,少しみにくいが "Move disk ..." の部分だけ追っていくと # ハノイの塔の答えがでていることがわかる xxx=hanoi2(3, "A", "B", "C") [[[[], "Move disk 1 from A to B", []], "Move disk 2 from A to C", [[], "Move disk 1 from B to C", []]], "Move disk 3 from A to B", [[[], "Move disk 1 from C to A", []], "Move disk 2 from C to B", [[], "Move disk 1 from A to B", []]]] # このバージョンでは 100 個の円盤でも一瞬.再帰呼び出しは 595 回. xxx=hanoi2(100, "A", "B", "C") ; nil $count2 595
一応,タプリング戦略によるプログラム変換のバージョンもこの形に してみよう.
defhanoi3(n, a, b, c) $count3 = 0hanoi_triple(n, a, b, c) [0] end defhanoi_triple(n, a, b, c) $count3 += 1 if n == 0 then [[], [], []] else x =hanoi_triple(n-1, a, c, b) [[x[0], "Move disk " + n.to_s + " from " + a + " to " + b, x[1]], [x[2], "Move disk " + n.to_s + " from " + b + " to " + c, x[0]], [x[1], "Move disk " + n.to_s + " from " + c + " to " + a, x[2]]] end endhanoi3(3, "A", "B", "C") [[[[], "Move disk 1 from A to B", []], "Move disk 2 from A to C", [[], "Move disk 1 from B to C", []]], "Move disk 3 from A to B", [[[], "Move disk 1 from C to A", []], "Move disk 2 from C to B", [[], "Move disk 1 from A to B", []]]] # n=1000 でも大丈夫です.移動操作列は 21000 - 1hanoi3(1000, "A", "B", "C") ; nil $count3 1001
意味があるかどうか分からないが,n=1000 の時の円盤移動操作の長さは
21000 - 1 = 10715086071862673209484250490600018105614048117055 33607443750388370351051124936122493198378815695858 12759467291755314682518714528569231404359845775746 98574803934567774824230985421074605062371141877954 18215304647498358194126739876755916554394607706291 45711964776865421676604298316526243868372056680693 75と302 桁の数になる( 1 行に 50 桁書いてある).
結果に空配列があるのが見苦しいので,そこだけは取り去ってみよう.
defhanoi3(n, a, b, c) $count3 = 0hanoi_triple(n, a, b, c) [0] end defhanoi_triple(n, a, b, c) $count3 += 1 if n == 1 then ["Move disk " + n.to_s + " from " + a + " to " + b, "Move disk " + n.to_s + " from " + b + " to " + c, "Move disk " + n.to_s + " from " + c + " to " + a] else x =hanoi_triple(n-1, a, c, b) [[x[0], "Move disk " + n.to_s + " from " + a + " to " + b, x[1]], [x[2], "Move disk " + n.to_s + " from " + b + " to " + c, x[0]], [x[1], "Move disk " + n.to_s + " from " + c + " to " + a, x[2]]] end endhanoi3(3, "A", "B", "C") [["Move disk 1 from A to B", "Move disk 2 from A to C", "Move disk 1 from B to C"], "Move disk 3 from A to B", ["Move disk 1 from C to A", "Move disk 2 from C to B", "Move disk 1 from A to B"]]
しかし,ここで読者には疑問というか不満があるに違いない.「本来, 解は線形の配列(またはリスト)で表現されていたのに,ここでやった ようにかなり深くネストして表現されていて良いのだろうか?」と. これを人の目に分かりやすく見せるためには,配列のネストを解いて, 一次元に並べる必要があり,その作業を残して,解を得たと言えるのだろうか. まだ,解答の途中なのではないだろうかと.
実は私もこれは疑問のままである.例えば,遅延評価の機構を持った 言語でハノイの塔を普通に再帰的に解くと,まったく具体的な計算を行わずに 計算が終わり,結果の中の,例えば3番目の移動操作を調べに行ったところで 始めて必要な計算がなされ,その移動操作がユーザに提示される. このとき,最初の解を求めるプログラムの計算量は O(1) と言えるのだろうか? 今回提示した解でのネストを許したものが解と言えるなら,こちらも 解と言えるような気もする.違うところがあるとするなら,我々がやった方は,
くらいである.移動操作に関しては,具体的な操作まで完全に求められているのに 対して,遅延評価のプログラムの場合は,それらがまだ計算されていないと いうこと
今回の実験や考察は,「計算」というものに対する何か深遠なるものを 我々に投げかけているような気もするし,案外,たわいもない話なのかもしれない. もしかしたら.この問題で求められるものが何かということがぶれているだけの ことかもしれない.
私の( Akihiko Koga) も, 探したら PDF が見つかったのでリンクを貼っておく.かなり煩雑なのとタイポが あるので,ここの付録で簡単に解説した.

We studied the method of introducing an auxiliary function for tupleing strategy (semi-)automatically.
このページで行ったハノイの塔のプログラムのプログラム変換は参考文献の
Akihiko, Koga : On Program Transformation with Tupling Technique, RIMS Symposia on Software Science and Engineering ||, 1983 and 1984: Kyoto, Japan, Lecture Notes in Computer Science 220, 1985, pp. 212-232によったものである.自分で言うのもなんだが,その論文は
上に書いたような30数年前の失敗を避けるために,ここでは
なお,「背景と目的」は,このページの場合,すでに読者は動機づけられているように思ったので 一番最後に回した.あまりプログラム変換に詳しくない人は, そちら から読むのがよいと思う.
最初に述べたようにここでは一つの関数を再帰定義する場合だけを扱う.対象とする プログラムの記述言語は特に具体的なものは与えない.なんとなく,関数型言語っぽい 記述で,if や where などの構文を持つものを想定する.また,それらの意味は 出てきたところで適宜説明する.実際に適用する場合には, 利用者が,適宜,そのとき使う言語で提供されるものに置き換えて欲しい.
対象とするプログラムは次の形をしているとする(<= の左辺が右辺で定義されているという意図である).
f(x) <= Φ(f(σ1(x)), ..., f(σn(x))) ここでΦ(...) は,一般には関数適用や if 文を含んだプログラムで, σ1, ..., σn は,x に対する何らかの既知関数とする.
ここでは定義される関数は
このような関数定義の例としては,
fib(n) <= if (n=0 or n=1) then 1 else fib(n-1) + fib(n-2) end
ここで,我々が考えるプログラミング言語は
if ... then ... else ... end
というような構文があり,常識的な意味を持っていると思ってほしい.
などで,この場合のσ1, ..., σn は
σ1 = λn.n-1ここで,λx.Φ(x) は引数 x をもらい,Φ(x) を返す関数を表す記法で,
σ2 = λn.n-2 = σ1・σ1=σ12
この例を最初に書いた対象プログラムの図式で書くと
fib(n) = Φ(fib(σ1(n) ), fib(σ12(n)) )
この大雑把な図式の表すところは,
の部分である.次の章では,{σ1,σ12}
ちなみにフィボナッチ数を求めるプログラムは次のように fib(n) と fib(n-1) の
対(タプル)を同時に計算する関数
fib(n) <= u where [u, v] =fib_pair(n) fib_pair(n) <= if (n = 0 or n = 1) then [1, 1] else [u+v, u] where [u, v] =fib_pair(n-1) end ここで,[u, v] は,値 u と v の組(タプル)を表し,u where [u, v] = fib_pair(n) は,まず,fib_pair(n) を 呼び出して,その結果で u と v を決めて,その変数設定のもとに u を返すと読んで下さい.fib_pair(n) の中で使われている where も 同様の意味です.
このときの関数の呼び出し関係は,後回しにした 「背景と目的」 にあるので,計算オーダーの違いを イメージしにくい人はそこを見て欲しい.
ここでは,「再帰関数の呼び出し関係から,タプリング戦略のプログラム変換で使える 補助関数を表すタプルの候補を見つける問題」を定式化する.
プログラム
f(x) <= Φ(f(に対して,関数の集合σ1(x) ), ..., f(σn(x) ))
を,その{σ1, ..., σn}
以後,f の引数に適用される関数 σ1, ..., σn などを,
σ1・σ1, σ2・σ1, ... など,色々な組み合わせで合成して,タプルの候補を探すことになる.したがって,これらの
関数が合成されてできる空間を固定しておくと考えやすい.
このような空間は
さらに,すべての要素に逆元が存在すれば
以下の議論では,
いくつか,関数の集合がなすモノイドに対する記法を定義しておく.
M を我々が考えている関数のモノイドとする.σ, ρ ∈ M,A, B ⊆ M, n を 0 以上の整数とするとき,これらの演算を次のように定義する.
注意:AB やσA などは,モノイドの掛け算が行われていることを強調したいときは, 間に「・」を入れて,A・B, σ・A などと表すこともある.
最後に,タプリング戦略でのプログラム変換の際に導入する
D = {σ1, ..., σn} を依存性とし,M を D ⊆ M なるモノイドとする.
A ⊆ M と T ⊆ M の組
特に |A| = 1 の場合は重要なので,その場合の c-タプルを
依存性 D に対して,c-タプル (A, T) が見つかったときの,それぞれの集合の要素間の 関係を次の図2.1に示す.T の中の各要素 τ は,
のどちらかの条件を満たす.つまり,T の要素は,Tα1, ..., Tαmの要素を使って,依存関係 D を使い,すべて定義することができるという条件を 満たしている.
c-タプル (A, T) は,タプリング戦略で,もとの再帰定義を書き換える タプルの候補を意図している.2つの成分のうち,T の方がタプルの形の補助関数
を表している.A = {α1, ..., αm} とすれば, 補助関数 h(x) は,何らかの記述 Φ を使って,
と,再帰的に書き換えられるわけである.この再帰定義Φの中ではもちろん再帰が 止まる条件などが if 文などを使って書き込まれているとする.
このように,新しい再帰関数を定義するとき,再帰をA の元に関して 書くことを意図しているので,f(x) を計算するのに,A の元を組み合わせていって 再度 f(x) を計算することになる状況,つまり,計算が循環してしまうことは望ましくない. これを禁止するのに3番目の条件
を付けている.
c-タプル (A, T) が見つかったとする.しかし,読者は,このような
プログラムの書き換えを行ったとき,引数に対する色々な関数適用の組み合わせがなされ,
元の定義では呼び出されなかった引数の値に対して計算が要求されるかもしれない
という心配を持つかもしれない.これは妥当な心配であるが,当面は,記述 Φ を
うまく行うことによって
c-タプルの中で,A が唯一の要素からなるとき(singleton set であるとき)は,
1つだけの再帰呼び出ししか持たない再帰関数に変換できる可能性があると
いうことであり,特に重要である.この場合は,もとの指数関数的な計算量が
線形のオーダーの計算量になる
可能性がある.この場合の c-タプルを,
例
先の例のフィボナッチ関数の依存性は D = {σ, σ2} だった.ここに,σ=λn.n-1 である.次のものはこの D の c-タプルである.
c-タプル (A, T) の意図としては,T が補助関数として導入するタプルを表し, A は,それを再帰定義として表すとき,再帰的に呼ぶ引数に適用する関数の集合を 表している.したがって,フィボナッチの例だと,(A, T) = ({σ}, {id, σ})
fib_pair(n) = [fib(id(n)), fib(σ(n))] = [fib(n), fib(n-1)]
を意図するタプルを導入し,それを
fib(n) <= u where [u, v] = fib_pair(n) fib_pair(n) <= if n < 2 then [1, 1] else [u+v, u] where [u, v] = fib_pair(n-1) end
である.この場合は,元の指数関数的な計算量が線形の計算量に改善されている.
ここではc-タプルを見つけるための色々なノウハウ,つまり,どんなときに存在するか,どんなときにある種のc-タプルが存在しないかなどのノウハウを定理の形として述べる. 特に証明に興味のない方は,まず,定理とその後ろにある応用例を見ていき,あとで,証明を 追いかけてみてもよい.
D を依存性とする.s →∞ としたとき,
|∪ i=0 to s Di| / s →∞
ならば,リニア c-タプルは存在しない.
[Proof] この依存性 D にリニア c-タプル ({α}, T) が存在したとする. |T| = B とするとき,s ≥ 0 に対して, Ds ⊆ ∪i = 0 to B・s(T・αi) が s に関する帰納法で証明することができる. したがって,D にリニア c-タプルがあれば, ∪ i=0 to s Di ⊆ ∪i = 0 to B・s(T・αi) となりる.右辺の集合のサイズは,高々 |T|・s・B にしかならないので, ∪ i=0 to s Di は,高々,s に対して線形でしか大きくならない.[Q.E.D.]
例えば,n 個の中から m 個を取り出す組み合わせの数 C(n, m) は次の漸化式で 表される.
C(n, m) = C(n-1, m-1) + C(n-1, m) if 0 < m and m < n
= 1 otherwise
この依存性は D = {λ(n, m).(n-1, m-1), λ(n, m).(n-1, m)} で |∪ Ds| は,s より大きなオーダーで増えていくので, リニア c-タプルはない.
次の定理は一見複雑な依存性を,より簡単な依存性に簡約化して c-タプルを 探すことを可能にする.
D を依存性とし,M を考察している関数空間のモノイドとする.さらに,M がある 有限モノイド F とモノイド M' の直積 F × M' として表せるとする.つまり,
M = M' × F for a monoid F such that |F| < ∞
D の M' 成分を D' とするとき.もし D' に c-タプル (A', T') があるなら,ただし,二つモノイド M' と F の直積 M' × F は,集合としての直積 M' × F に次の演算を定義したモノイドとする.
(x1, y2)・(x2, y2) := (x1・y1, x2・y2)
for (x1, y1), (x2, y2) ∈ M'×F
また,D ⊆ M' × F の M' 成分 D' は,次の依存性とする.
D' := {x | (x, y) ∈ M' × F}
この定理は,依存性から c-タプルを探すとき,その依存性の 有限モノイドの直積成分は取り去って考えて構わないことを示している. 例えば,ハノイの塔のプログラム[Proof] M' をモノイド,F を有限モノイドとし, M = M' × F = {(a, b) | a ∈ M', b ∈ F} (a1, b1)・(a2, b2) = (a1・a2, b1・ b2) とする. (A', T') が D' = {σ | (σ, b) ∈ D} の c-タプルとするとき, (A' × {id}, T' × F) は D の c-タプルであることを示す. まず,id ∈ A' だから,(id, id) ∈ A' × {id}. 次に,(σ, b) ∈ T' × F とする. σ ∈ T'A' の場合は,(σ, b) ∈ (T' × F)・(A' × {id}) D'σ ⊆ T'A' の場合は,D(σ, b) ⊆ (T' × F)・(A' × {id}) となり,条件2も満たす. 最後に,s > 0 に対して,A's が id を含まないので,(A' × {id})s も (id, id) を含まない.[Q.E.D.]
hanoi(n, a, b, c) <= if n = 0 then nil
else hanoi(n-1, a, c, b) +
[["Move disk", n, "from", a, "to", b]] +
hanoi(n-1, c, b, a)
ここで,"+" は配列を連結する演算子として使っているの例では,依存性は,
D={λ(n, a, b, c).(n-1, a, c, b), λ(n, a, b, c). (n-1, c, b, a)}
であり,この後ろの方3つのパラメータ a, b, c の部分は,3つのものを入れ替える対称群と同型である.
3つの場所 a, b, c を入れ替える関数のなす群を S3 と表すことにすると,
考察している関数空間のモノイド M は,Z × S3と同型である
(この場合は全部逆元を持つので群でもある).
|S3| = 6 < ∞ であるから,この定理が適用できる.
D の S3に関する商をとった依存性(つまり,D から,a, b, c の部分を除いた依存性)
D'={λn.(n-1)}
は,あたりまえの c-タプル (A, T) =
({λn.(n-1)} × {id}, {id} × S3)
がある.要は,a, b, c 3つの場所のすべての入れ替えについてハノイの塔の
解を求める関数を定義すると,毎回の計算は,一つ円盤を少なくしたハノイの
塔の解から作ることができるということである.本ページの前半では6つではなく
3つの組からなるタプルでプログラム変換を行っている.この方法は後で述べるが,
この定理は,とにかく,原理的には有限モノイドの因子を取り除くことができることを表している.
次の定理はリニア c-タプルが存在する十分条件であり,ある場合における,定理3.1(リニア c-タプルが存在する必要条件) の逆の定理である.その場合とは,M が有限生成のアーベル群(可換群)である場合である.
考察している関数空間のモノイド M が可換群であるとする(もともと,モノイド というところまでしか要求していなが,ここではたまたま可換群までの条件を 満たしていたとする).依存性 D が
|∪ Dn|/n が有界
なら,D にはあるα∈Mに対して,リニア c-タプル ({α}, T) が存在する.
これが成立することの概要を説明しておく.依存性 D を含む最小の M が(有限生成の)可換群なら, これは整数のなす群 Zいくつかと,有限可換群の直積であらわされる.上の式が 有界になるためには,整数の群 Z の成分は高々1つしかない.したがって,M は F × Z ここで F はある有限可換群 という形に書き表される.この関数の空間にはリニア c-タプルがある.[Proof 概略]
次の定理は,このページでハノイの塔のプログラムを,3項組を使い変換するのに 使った定理である.[Q.E.D.]
依存性 D が
[Proof] |Ds+1| = |Ds| とし,α ∈ D は逆元 α-1 ∈ M を持つとする. Dsα ⊆ Ds+1 だが,これらは要素数が等しいので Dsα = Ds+1 である.したがって,任意の σ ∈ T = Dsα-s に対して, Dσ ⊆ DT = D(Dsα-s) =(Ds+1α-s = Dsαα-s = (Dsα-s)α = Tα これは,c-タプルの条件の2番目 Dσ ∈ TA を満たす. また,αs ∈ Ds だから,id = αs・α-s ∈ Dsα-s = T となり, 一番目の条件も満たしている. αs は s>0 に対して id にはならないので3番目の条件も満たしている.[Q.E.D.]
本ページの本文の方で使ったハノイの塔のタプルは,この定理を使って求めている. ハノイの塔の依存性は,
D={λ(n, a, b, c).(n-1, a, c, b), λ(n, a, b, c). (n-1, c, b, a)}
だが,この依存性のべき乗 Ds は3以上に増えない.
|D| = 2, |D2|=3, |D3|=3, ...
である.したがって,λ(n, a, b, c).(n-1, a, c, b) をσと書いたとき,リニア c-タプル
({σ}, D2・σ-2) =
({λ(n, a, b, c).(n-1, a, c, b)}, {λ(n, a, b, c).(n, a, b, c)=id,
λ(n, a, b, c).(n, b, c, a),
λ(n, a, b, c).(n, c, a, b)})
を使ってリニアな再帰定義
hanoi(n, a, b, c) <= u where [u, v, w] = hanoi_triple(n, a, b, c)
hanoi_triple(n, a, b, c) <=
if n = 0 then [nil, nil, nil]
else
[u + [["Move disk", n, "from", a, "to", b]] + v,
w + [["Move disk", n, "from", b, "to", c]] + u,
v + [["Move disk", n, "from", c, "to", a]] + w]
where [u, v, w] = hanoi_triple(n-1, a, c, b)
end
に変換できる.
考察している関数空間のモノイド M の部分集合 B ⊆ M があって, D ⊆ [B] (つまり,D が B で生成されるモノイド [B] に入っている) が成立し, s > 0 に対して Bs が id を含まないなら,D は (B, T) の形の c-タプルを持つ.ここで,この T は,
T := ∪ d∈D prefix(d)
ここで,d = σ1・...・σn σi∈B のとき,
prefix(d) = {id, σ1, σ1・σ2, ..., σ1・...・σn-1}
とする.つまり,関数を1つずつ右から剥がしていったものを
集めたものである.
で求められるものである.
この定理の一番簡単な適用対象はフィボナッチ数を求めるプログラムである.そのプログラムの 依存性 D は,[Proof] まず,id ∈ prefix(d) for d ∈ D であるから,c-タプルの1番目の条件は満たす. 次に,id 以外の σ &isin T について言えば,T には,σの右側の関数適用を剥がした 関数が入っているので,σ &isin TB となる.また,id についていえば D・id = D ⊆ TB であるから,c-タプルの2番目の条件は見たしている. 3番目の条件は定理の B の条件と一緒である.[Q.E.D.]
D = {σ, σ2} where σ=λn.n-1
だから
T = prefix(σ) ∪ prefix(σ2)
= {id} ∪ {id, σ}
= {id, σ}
となる.したがって,c-タプルは ({σ}, {id, σ}) = ({λn.n-1}, {id, λn.n-1}) で,
fib_pair(n) = [fib(n), fib(n-1)]という補助関数を定義し,これを fib_pair(σ(n)) = fib_pair(n-1) を参照する再帰関数に 書き直せばよいことがわかる.
生成元の集合 B が2個以上の場合も例を載せておく.
f(x) <= if P(x) then h(x)
else
list(f(car(cdr(cdr(x))), f(car(car(car(x))), f(cdr(cdr(x))))
end
ここで,P(x), h(x), car(x), cdr(x) は何らかの既知関数とする.
この依存性は
D = {λx.car(cdr(cdr(x))), λx.car(car(car(x))), λx.cdr(cdr(x))}
c-タプルは
T = prefix(car・cdr・cdr) ∪ prefix(car・car・car) ∪ prefix(cdr・cdr)}
= {id, car, car・cdr} ∪ {id, car, car・car} ∪ {id, cdr}
= {id, car, cdr, car・cdr, car・car}
A = {car, cdr}
である.もともと,3つの再帰呼び出しを持っていた関数定義だが,同時にいくつかの
引数に対して計算を行うことにより,2つの再帰呼び出しだけですむようになっている.
生成元の集合 B が2個以上の場合は,B が1個の集合である fib の場合ほど効果はない.もちろん,3つの再帰呼び出しを持つ再帰関数が,2個の再帰呼び出しに抑えられればそれなりの効果はあるが,やはり 指数関数的に計算量が増えてしまうので,50歩100歩の感は否めない.
2018年 7 月 16 日(月))
ここでは,c-タプルが見つかったときの,もとのプログラムの書き換え方法について 少し具体的に述べる.
もとのプログラムは次のような形をしているとする.
f(x) <= if P(x) then a(x) else Φ(f(σ1 (x)), ..., f(σs (x))) end
書き換えの時に停止性の問題が発生するので,ここでは,最初の大雑把な定式化より 一段階詳細にして,再帰呼び出しを行わない部分を明示的に書いている.この依存性は
D = {σ1, ..., σs}
である.これに対して,c-タプル
A = {α1, ..., αm}
T = {τ1, ..., τn}
が見つかったとする.このときのプログラムの書き換えでは,補助関数 h(x) は
h(x) = [f(τ1 (x), ..., τn (x)]
を意図する関数を導入する.τi = id とすれば,元の関数 f(x) は
f(x) = ui where [u1, ..., ui, ..., un] = h(x)
と書き換えられる.あとは,h(x) を自分自身を参照する再帰関数に書き換えるだけである.
h(x) の記述方法は大まかに言って2つの方法がある.一つは
書き換え方法1(人間による書き換えに向いている)
h(x) <= if P'(x) then [t1(x), ..., tn(x)] else [ψ1(u1, ..., um), ..., ψn(u1, ..., um)) where u1 = h(α1(x)) ... um = h(αm(x)) end
ここで,P'(x) は再帰を止めるための条件である.もともとの P(x) から変化しているのは 今回は f(x) を計算するためだけでなく,タプルに対して止める必要があるからである. t1(x), ..., tm(x) は,その時の h(x) のタプルの各要素を計算する ための何らかの式である.これらは定義式を見ながら人間が「うーん」と考える.ψi(u1, ..., um) は,u1, ..., um を 使った式であるが,これはτiがT·Aに含まれている場合は,どれかの ujの要素,そうでないときは,u1, ..., um の要素を Φで組み合わせた式である.厳密に書くと次のようになる.
Ψi = uj[k] τi∈T·A の場合
ここで j, k は次を満たす添え字とする τi = τj·αk∈T·A
= Φ(v1, ..., vs) その他の場合
ここで vj = uk[l] ただし σj·τi = τk·αl
この例としては すでに一度出てきたが,フィボナッチ関数の例が典型的である.fib(n) の元の定義は
fib(n) <= if (n=0 or n=1) then 1 else fib(n-1) + fib(n-2) end (*)
であり,この依存性 D = {λn.n-1, λn.n-2} には c-タプル
(A, T) = ({λn.n-1}, {id, λn.n-1})
があるので,補助関数を
fib_pair(n) = [fib(n), fib(n-1)]
とおき,次のように書き換えることができる.
fib(n) <= u where [u, v] = fib_pair(n)
fib_pair(n) <= if (n = 0 or n = 1) then [1, 1]
else
[u+v, u] where [u, v] = fib_pair(n-1)
end
実はここに少し「ごまかし」がある.
としている部分である.fib(-1) はもともとの定義 (*) では定義されていなかった.それを 無理やり1つの if 文の then の部分に入れて,fib(-1) = 1 としているのである.この例から ほころびが見つかり,読者は次のような疑問を持つだろう.
これはすごくまともな疑問である.実際に上の疑問のような場合が生じる. これには,もう一つの書き換え方法を述べた後にまとめて筆者の考えを述べる.
もう一つ書き換えの方法を書いておく.以下の表記で,
Ψi は先の書き換え方法1と同様に次のように定義される.
Ψi = uj[k] τi∈T·A の場合
ここで j, k は次を満たす添え字とする τi = τj·αk∈T·A
= Φ(v1, ..., vs) その他の場合
ここで vj = uk[l] ただし σj·τi = τk·αl
この定義のもとに,元のプログラムを次のように書き換える.
書き換え方法2(機械的な書き換えに向いている)
h(x) = [if P(τ1(x)) then a(τ1(x)) else Ψ1 end, ... if P(τn(x)) then a(τ1(x)) else Ψn end] where where u1 = h(α1(x)) ... um = h(αm(x))
方法1でも方法2でも良いので,f(x) を呼び出したとき,その計算でどのような項が 計算されるか,タプルの要素単位で追跡してみよう(図4.1,図4.2 を参照).実際のプログラムでの追跡でなく, 依存性 D, c-タプル (A, T) の要素の形で追跡してみる.
最初,f(x) が呼び出されると, h(x) の中の id ∈ T に対応する項が評価される.(T, A) が c-タプルであることから, D・id = D ⊆ T・A なので,T・A の中の D に対応するf() の値が計算されることになる. この時点では,まだ,もともと呼ばれたはずの f(σ(x)) に対する呼び出ししか参照 されていない.次に 今参照されたタプルの要素 f(σ(x)) がまだ計算されていないときは, σ が, T・A2 にあるか,あるいは,D・σが T・A2 にあるかに より,それらに対応する T・A2の関数に対する f() が計算される.毎回, 元の関数の評価に必要な分しか参照されないので,帰納法により,もとの定義で計算された f(σ(x)) に対応する値しか参照されないことになる.
方法2は止まらないと言ったが,タプルの要素単位で評価の駆動を掛けることができる 遅延評価の機構を持っている実行系では停止し,もともとの定義で評価される f(σ(x)) だけが評価されるはずである.さらに計算効率は,書き直した後では,複数の場所で 現れる同じ f(σ(x)) が共有されているので,もとの定義のように組織的に同じ引数に対する 呼び出しがおこるということはなくなる.
つまり,結論としては,
本論文では,タプリング戦略に基づくプログラム変換の自動化のネックになっていた,補助関数の 導入の自動化を目指して,モノイドの言葉を使い,補助関数の定義に有効なタプルの候補を 見つけ出す問題を定式化した.
もとのプログラムの再帰呼び出しの際に,引数を変化させている関数から生成される モノイドをM として,M の性質と補助関数導入の候補の関係を論じる.具体的には, もとの再帰呼び出しで引数を変化させていた,関数の集合を「依存性」D として定義し, D に対して,補助関数 T と書き換えられた再帰プログラムで再帰呼び出しのときの 引数の変化を指示する関数の集合 A を決める問題を定式化した.
定式化された問題に対して,依存性 D の特徴により,補助関数の候補 (A, T) を 見つけ出す方法をいくつかの定理として整理した.
この整理によりハノイの塔の問題などに対して,効果的な補助関数を容易に 見つけ出すことができるようになった.
また,見つけた補助関数を用いてプログラム変換する際に,もとの プログラム呼び出しでは扱わなかった引数を変化させる関数を扱う可能性が あることを述べ,それに対する対応方法を述べた.
これらにより,タプリング戦略を用いたプログラム変換の補助関数導入が容易に なり,モノイドの計算が自動でできるような場合は,自動的な導入が可能になると 考える.
もう一つ,計算の重複を避ける方法としては,メモ化により,一度計算した結果を 覚えておき,それを再利用するという方法がある.これは,本ページの最初の記事の 中でも使って入り,非常に簡単な方法である.ただし,この方法は引数の空間が 適当に小さな空間であることが要求される.タプリング戦略を用いたプログラム変換では 再帰関数定義の見直しにより,できるだけ同じ引数に対する呼び出しをしないように するので,そのような大きなメモリー空間は必要ない.その代わり,変換が大変なことと 必ずしもすべてを共有できるわけではないというトレードオフがある.
で紹介している
A. J. Cain's "Nine Chapters on the Semigroup Art"
はとても良い教科書である.
ここの解説は参考文献に書いた次の論文を概ね簡単にした内容である.
もう一つ,c-タプルをここでは
常にという訳ではないが,プログラムを人間に分かりやすく,その問題の定義に近い形で記述した場合にプログラムの
実行性能が著しく悪くなることがある.そのような場合,もとの分かりやすい記述から,
プログラム変換と呼ばれるプログラムの同値変換の技術を使って,効率的なプログラムに
変換する方法が知られている[これらの技術の参考文献については,本ページの本文の
参考文献
を参照のこと.これは本論文を書いた当時のものなので,現在はさらに多くの検討が行われ,
多くの知識が蓄積されている.これらについては,「プログラム変換」というキーワードで
検索してほしい].
例えば,次のようなフィボナッチ数を求める再帰プログラム
は人間には分かりやすいが,非常に効率が悪い.
実際,例えば,fib(5) を計算してみると次の図のような関数の呼び出しが起こり,引数の
大きさに対して指数関数的な実行時間がかかってしまう.
この呼び出しグラフをよく見ると,次の図のように,同じ呼び出しが組織的に複数行われることによって
非効率性が起こっていることが分かる.例えば,fib(3) の計算は単独でも,また,fib(4) の
計算の中でも起こっていて,それぞれの中に含まれる fib(2) の計算もまた,それぞれの中で
複数発生している.
これら同じ計算を共有してやることにより,このプログラムの実行は引数の
大きさに線形なものにすることができる.このような最適化としてタプリング戦略による
プログラムの変換が知られている.タプリングとは n-項組を作るということを意味している.
天下り式だが,次のような補助的な関数を考えてみる.
ここで,引数を n-1 にして,fib_pair(n-1) を考えてみると,
もとの定義 (1) を使うことにより,
のように自分自身を参照するプログラムに書き直すことができる.こちらのプログラムでは
計算量は n に線形になる.このプログラムの関数の呼び出し関係を次の図に示す.
左側の fib_pair は,fib_pair(n) が fib_pair(n-1) を1つだけ呼んでいるので,
これは n に比例した回数しか呼び出されない.右側は,その2項組の中の値の依存関係を
示している.こちらは,(1) では,同じ n に対する fib(n) が複数計算されていたのに
対して,こちらでは1つに共有されており,これにより,指数関数的な計算量が線形な計算量に
効率化されている(注意1).
このようにプログラム変換を用いた効率化では,計算量のオーダーが変化するような
劇的な効率化ができることが多いのだが,途中で天下り式に与えた補助関数
の定義を人間が与える必要があった.実際,伝統的なプログラム変換の技術の中で,
このような補助関数の導入は,
EUREKA STEP (発見的なステップ) と呼ばれ,プログラム変換の自動的な
適用の障害になるものであった.
本論文では,上に述べた fib(n) のようなタプリング戦略に基づくプログラム変換の
EUREKA STEP の自動化を目指す.フィボナッチの例では,補助関数の導入は,
fib(n) の計算が,fib(n-1) と fib(n-2) に依存していることで決まって来る.
つまり,
という関係が本質的な部分である.さらにいうなら,これは n-1, n-2 でなくとも,引数を
変化させる任意の関数σについてσ(n), σ2(n) に変わっても,同様の変換が
可能であることが予想できる.本論文では,この本質的な部分をモノイド(ある場合は群)
の言葉を使って定式化し,タプリング戦略に有効な補助関数の導入のための知識を整理する.
本論文の目的はプログラム変換に有効な補助関数の自動的な導入だが,上にのべたように
任意のモノイドで定式化してしまうと,語の問題(モノイドの中で成立するすべての等式を
自動的に導くアルゴリズムは存在しない)があり,完全な自動化はできない.しかし,
語の問題はまったく解けない訳ではなく,ある限定された状況では解ける場合もあるので,
このような本論文のように形式的な知識体系として,タプリング戦略の補助関数導入ノウハウを
整理することは意味のあることだと考える.
知り合いの
私はもともと scheme のプログラムはあまり書いたことが無いうえに,
今回書くのは20~30年ぶりくらいなので,scheme プログラムとしてはあまり
うまい表現ではないかもしれません.
一応,Windows 10 上に, Racket という処理系をインストールして動作を確かめました.
以下で実現した関数の意味は次の通りです.
以下は,結果を表示せず,再帰呼び出しの回数だけを返します.どの位計算に時間がかかっているかを確かめるための関数です.bar4, bar5 は n に 100 とか 1000 を
入れても大丈夫ですが,bar1, bar2, bar3 は,20 位にとどめておいてください.
うちの計算機はメモリーを 4GB 積んでいて,そこらあたりから少しずつ動作に
時間がかかるようになり,22, 23 では途中で止める必要がありました.計算機によっては,それ以下でも苦しいかも
しれませんので,
圏論を勉強しよう へ
上記の群に関する定理に関して,半群やモノイドでどのような定理が成り立つか,
知っていると本論文の拡張に役出す.
それには,
2つの元 x, y の演算 x・y が定義されている集合 S について
(S と演算・のペア (S, ・) と書くことも多い),S が
という.
(Differences from the original paper)
Akihiko, Koga : On Program Transformation with Tupling Technique, RIMS Symposia on Software Science and Engineering ||, 1983 and 1984: Kyoto, Japan, Lecture Notes in Computer Science 220, 1985, pp. 212-232
数理解析研究所講究録 (1985), 547: 128-155
ここにもとの論文との違いをまとめる.
元の論文は,
fiblist(n) <= if n < 0 then 0 else cons(fib(n), fiblist(n-1)) end
fib(n) <= if (n < 2) then 1 else fib(n-1) + fib(n-2) end
ここでは再帰呼び出しの際に
と定義したが,元の論文では,最初の条件を
としていた.これは最初から T には id が入っているという少し強い条件で
定義を簡略化することにした.
今回,
fib(n) <= if (n=0 or n=1) then 1 else fib(n-1) + fib(n-2) end (1)
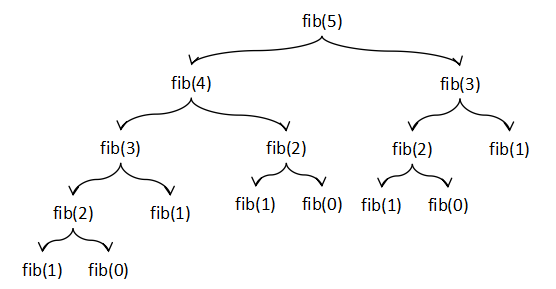
図I-1 フィボナッチ数を求める素朴な再帰関数のコールグラフ
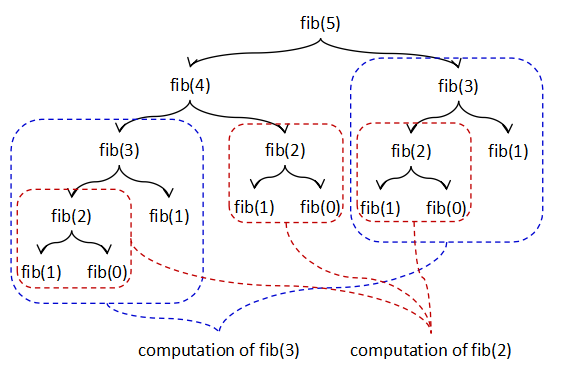
図I-2 フィボナッチ数計算における計算の重複
fib_pair(n) = [fib(n), fib(n-1)] (2)
ここで [a, b] は a と b の組を表すものとする.
fib_pair(n-1) = [fib(n-1), fib(n-2)] (3)
fib(n) = u where [u, v] = fib_pair(n) (4)
fib_pair(n) = if n = 0 or n = 1 then [1, 1]
else [u + v, u]
where [u, v] = fib_pair(n-1)
end
ここで Exp1(x) where x = Exp2 は,まず,式 Exp2 を計算して,その
結果を x として,その上で式 Exp1(x) を評価することを表す.
Exp1(x) の x は,式 Exp1 が変数 x に依存していることを表す意図で
書いている.

図I-3 フィボナッチ数の計算の重複の除去
fib_pair(n-1) = [fib(n-1), fib(n-2)] (3)
n に対する fib を求めるためには n-1 と n-2 に対する fib が求まって入れば良い.
付録 B. Scheme によるhanoi(高速版等)のプログラムの記述
(Hanoi programs rewritten in 'scheme')

普通の再帰的なハノイの塔のプログラムです.(hanoi 3 "A" "B" "C") のように呼び出され,結果として円盤をすべて "A" から "B" へ移すための個々の円盤の移動動作のリストを返します.
メモ化により,重複計算を除去したハノイの塔のプログラムです.
タプリング戦略のプログラム変換で重複計算を除去したハノイの塔のプログラムです.
メモ化の hanoi2 の append 除去版です.
タプリング戦略のプログラム変換版 hanoi3 の append 除去版です.
;;; 普通のハノイの塔のプログラム
(define count1 0)
(define (
計算機(主にソフトウェア)の話題 へ
束論を勉強しよう へ
半群論を勉強しよう へ
ホームページトップ(Top of My Homepage)