記載場所は次の通り.
- プログラムの動かし方
ちょっと動かしてみる - :l2c コマンドについて
ラムダ式から SKI コンビネータ式への変換トレース機能(追加)
Youtube にこのプログラムの動かし方の説明をあげた. 2022.08.09 (火)
ラムダ式を SKI コンビネータの式に変換する過程を表示するプログラムの動かし方 ... 11分36秒
λ式から SKI を使った式への変換のトレース
 一か月ほど前(2018年6月20日(水)),とある勉強会でコンビネータ論理を教えてもらった.
その勉強会は,
一か月ほど前(2018年6月20日(水)),とある勉強会でコンビネータ論理を教えてもらった.
その勉強会は,
SKI のコンビネータで帰納的関数が表現できることを示して, コンビネータ論理の真な等式の集合は計算可能でないことを示すという内容だったのだが, その予習として Wikipedia などを調べて,コンビネータの式のインタープリタと ラムダ式からSKIを使った式への変換機能を Ruby で組んでみた.そのとき作ったλ式から SKI コンビネータの式への変換プログラムは変換の過程(トレース)を出すようにしていたのだが, その出力が結構分かりやすいと思ったので,ここにいくつかログを載せておく.
補足: 簡単なコンビネータのインタープリタを提供することにした.詳しくは SKIコンビネータ AGAIN を参照されたい.あちらはコンビネータの理屈はあまり書いてなく, ただ動かしてみて遊ぶというものなので, こちらで勉強して,あちらで実際に動かしてみると言うのが良いと思う. 2019.02.11 (月)
補足2: ここで述べたラムダ式から SKI コンビネータの式へ変換する過程を表示する機能 :l2c を SKIコンビネータ AGAIN のプログラムに組み込んだ.したがって,実際に動かしてみたいという人は, あちらのプログラムを動かしてみるのが良いと思う.しかし,変換の理論などの話は こちらにあり,あちらは,どちらかというと SKI コンビネータを動かして遊ぶという 趣旨で作ってある.記載場所は次の通り.
2022.08.08 (月)
- プログラムの動かし方
ちょっと動かしてみる
- :l2c コマンドについて
ラムダ式から SKI コンビネータ式への変換トレース機能(追加)Youtube にこのプログラムの動かし方の説明をあげた. 2022.08.09 (火)
ラムダ式を SKI コンビネータの式に変換する過程を表示するプログラムの動かし方 ... 11分36秒
変換式は何段階かの適用の形で表現される場合が多い.若干,先ばしることになるが, ((S x) y) z という形が現れたら,それを (x z) (y z) に置き換えてよいなどである.
コンビネータの間の空白は普通書かないらしい.ここでは,私が予習でコンビネータの インタープリタを作ったときの都合で,普通省略される括弧も空白も書くことが多い.
S x y z = ((S x) y) z = (x z) (y z)
コンビネータの式は括弧を省略したら左から括ることになっているらしい.
直観的には,
S コンビネータは,
数式だと中々意味を取りにくい人もいると思うので,少し例えを交えて書いておく. S さんは,x さんと y さんからなる部署の責任者と思えばよい.S さんの仕事は 部下の作業に必要な資源 z の調達と,調達した z の x さんと y さんへの 分配である.調達,分配が終われば,S さんの役割はなくなり,あとは,x さんと y さんが分配された資源 z を使って仕事をするだけである.
ここでは部下が2人の場合を述べたが,2人への分配ができれば,有限人なら
何人の部下への分配でもできる.
次のように3人に分配したいとする.
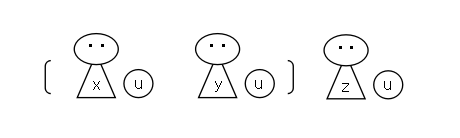
このときは,S を2回使って,次のようにすればよい.
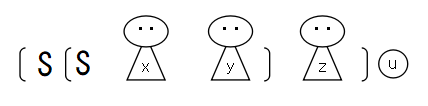
K x y = (K x ) y = x
直観的には,
 K の
K の
(K Exp) x = Exp
となる.つまり,(K Exp) は Exp を抱え込んでいて,何か受け取るといつでも
Exp を返す機能を持っている.
I x = x
これは,同じ意味のものが上の S と K を使ってかける.たとえば,
(S K K) x = ((S K) K) x = (K x) (K x) = x
となり,S K K は,(S K K) x = I x = x となり,I と同じは働きをする.上の式の
(K x) (K x) の2番目の (K x) は何であっても全体として式は x に簡略化されるので
((S K) S) も,I と同じ働きをする.このように S と K があれば,I は必要ないのだが,
次に,少し形式的にλ式を定義しておく.
可算無限個の変数記号の集合 V が与えられているとする.このとき,
λ式の作り方のルール2 は関数を作るルールで,ルール 3 は関数の適用を表している. 従って,意図としては,例えば
(λx.f x) (g y) = f (g y)
のように,左辺の意味は,一番目の式のλで指定された変数のところに,
2番目の式を代入した式を表している.こういう左辺から右辺への変換を
先のコンビネータ S, K, I は次のようにλ式で表される.
(S Exp1 Exp2) x = (Exp1 x) (Exp2 x)
これが x になるようにするには,Exp1 を K にすればよい.Exp2 が何でも
(K x) (Exp2 x) = x
になってしまう.ということで, S K K, S K S, S K (K K), ... これらはみんな I と同じ機能のコンビネータ式である.
つまり,(A x) y = y となるコンビネータ A を S, K, I の組み合わせで作れる だろうかという問題である.それには,コンビネータ S について,
((S u) x) y) = (u y) (x y)
であることと,K のもう一つの機能,つまり,第1引数を抱え込んで何が与えられても それを返すという機能に着目すれば,u を K と置けばよい.つまり,
((S K) x) y => (K y) (x y) => y
で,
もう一通り,この false に相当する SKI コンビネータ式の求め方を書いておく. この false はλ式で書くと,
false = λx.λy.y
である.この中の式 λy.y は, I である.したがって,
false = λx.I
となる.これは何が来ようと I を返す関数なので,K の説明の2番目の機能から,
とも書ける.
not = λx.((x false) true)
言い換えれば
not x = (x false) true
である.not の後ろに与えられた x を前の方の (x false) にもっていく必要がある. このようなことが出来るコンビネータとしては,S があった.
(S Something λu.true) x = (Something x) ((λu.true) x)
= (Something x) true
λu.true は定数関数だから,(K true) とやればよい. 後は,
Something x = x false
になる Something を求めればよい.これも S を 使えば,
Something x = (S I λu.false) x = (I x) ((λu. false) x) = x false
まとめると
となる.せっかく,インタープリタを作ったので,not を実行させてみよう.
SKI> not => (S ((S I) (K (K I)))) (K K) # not の定義 SKI> true => K # true の定義 SKI> false => K I # false の定義 SKI> not true # not true を評価 => ((S ((S I) (K (K I)))) (K K)) K => (((S I) (K (K I))) K) ((K K) K) # KがSにより2つの式に取り込まれた => ((I K) ((K (K I)) K)) K => (K (K I)) K => K I # K I = false になった SKI> not false # not false の評価 => ((S ((S I) (K (K I)))) (K K)) (K I) => (((S I) (K (K I))) (K I)) ((K K) (K I)) => ((I (K I)) ((K (K I)) (K I))) K => ((K I) (K I)) K => I K => K # true = K になった
以上,ちょっと長かったが,
or x y = if x then true else (if y then true else false)
である.後ろの if 文は,y が true, false だけのときは I で良い.(or x) は,x = true のときは,y に何が来ても true を返し,x = false の時は,y を返す関数を表す式,つまり,(x (K true) I) を返せばよい.
or x = x (K true) I = (S (λu.(u (K true))) (K I)) x
λu.(u (K true)) = S I (K (K true))
ということで,
SKI> :let or=(S (S I (K (K true))) (K I)) # or を定義 SKI> or true false => (((S ((S I) (K (K K)))) (K I)) K) (K I) => ((((S I) (K (K K))) K) ((K I) K)) (K I) => (((I K) ((K (K K)) K)) I) (K I) => ((K (K K)) I) (K I) => (K K) (K I) => K # or true false = K = true SKI> or false true => (((S ((S I) (K (K K)))) (K I)) (K I)) K => ((((S I) (K (K K))) (K I)) ((K I) (K I))) K => (((I (K I)) ((K (K K)) (K I))) I) K => (((K I) (K K)) I) K => (I I) K => I K => K # or false true = K = true SKI> or false false => (((S ((S I) (K (K K)))) (K I)) (K I)) (K I) => ((((S I) (K (K K))) (K I)) ((K I) (K I))) (K I) => (((I (K I)) ((K (K K)) (K I))) I) (K I) => (((K I) (K K)) I) (K I) => (I I) (K I) => I (K I) => K I # or false false = K I = false
((S I) (K x)) y = (I y) ((K x) y) = y x
また,S の分配機能と K の定数関数を作る機能を考えれば,
exchange x = (S (K (S I)) K) x = ((K (S I)) x) (K x) = ((S I) (K x))
と出来た.まとめると
exchange = (S (K (S I)) K)
である.
引数を2つの関数に分配する S を使って出来そうな 感じがする.で,その分配される関数を恒等関数 I にしてしまえば良い訳だ.
(S I I) x = (I x) (I x) = x x
ということで出来た.(S I I) に (S I I) を適用すると,
(S I I) (S I I) = (S I I) (S I I)
と,まったく同じものができるため,止まらなくなる.
このように S, K, I のコンビネータを組み合わせて色々な機能のコンビネータ式を 作ることができる.ここではブール値 true, false をある形にきめて,論理演算, not や or を作ってみたが,一般に,自然数の形を決めて,再帰関数の機能を 持つコンビネータ式を作ることができる.これらに興味のある人は後ろにあげた 参考文献などを参照してほしい.
x を Exp の中の色々なところに書くことに寄って, Exp2 をそこに代入できる機構は便利なのだが,変数名をうまく定めないと 違う意味で同じ名前が現れて紛らわしい.これは実際にプログラミング言語の 実装のときも問題になる.一方,コンビネータの方はパラメータを使わず, S で複数の箇所にばらまく.これは望みの場所に持っていくのに苦労は するが,パラメータ名の衝突の心配がない.ラムダ式とコンビネータ論理は このような長所・短所がある.
この引数を Exp1 にこの λx の構造がないときは単に 関数適用したという事実を表しているだけである.
Exp に x が現れる一番簡単な形は,λx.x でこれは恒等関数, コンビネータで言えば I である.
その他の場合としては,Exp が関数適用の形になっている場合と,さらに 他のλyが現れる場合である.
一方,SKI コンビネータで何ができるかというと,
K trans(Exp)
とすればよい.ここで trans(Exp) は,λ式 Exp を SKI のコンビネータ式に 変換した結果である(すでにこのことは言ったのだが,重要なことなので もう一度言う).ルールとして書いておくと,
となる.
(λx.(Exp1 Exp2) Exp = (λx.Exp1 Exp) (λx.Exp2 Exp)
であることを考えれば,S を使った式に変換できることが容易に分かると 思う.
である.
(trans(Exp1) trans(Exp2))
に置き換えればよい.ルールとしては
である.
まず,Ruby の対話型インタープリタ irb を起動し,SKI インタープリタを読みこんで, それを起動する.
C:\> irb
irb(main):001:0> load "ski.rb"
=> true
irb(main):002:0> top
+-------------------------------------------------+
| Welcome to Simple SKI Interpreter |
| |
| written by Akihiko Koga |
| Ver. 0.51 June 19th, 2018 |
+-------------------------------------------------+
Please type a combinator expression or a command (:help for help)
SKI>
雰囲気も出したいので,起動する部分から表示した.見事に CUI (Character-based User Interface) のツールである.
ここに適当に SKI コンビネータで書いた式を入力すると,SKI の 定義に従って計算していく(つまり, S, K, I の定義を適用していく).
まず,S, K, I の定義を思い出すために,それぞれの定義そのものの変換をさせてみた. このツールはコンビネータ式を読み込むと,それを次々にコンビネータの定義に従って変換して いき,その過程を => でつないで表示していく.
SKI> S x y z => ((S x) y) z => (x z) (y z) SKI> K x y => (K x) y => x SKI> I x => I x => x
少し複雑なものをやってみよう.
SKI> S K K x => ((S K) K) x => (K x) (K x) => x SKI> S K I x => ((S K) I) x => (K x) (I x) => x SKI> exchange => (S (K (S I))) K SKI> exchange x y => (((S (K (S I))) K) x) y => (((K (S I)) x) (K x)) y => ((S I) (K x)) y => (I y) ((K x) y) => y x SKI> S I I x => ((S I) I) x => (I x) (I x) => x x SKI> (S I I) (S I I) => ((S I) I) ((S I) I) => (I ((S I) I)) (I ((S I) I)) => ((S I) I) ((S I) I) *** Cycle detected
まず,最初のS K K だが,これは I と同じ機能を持つことを準備のところで述べた. 実際に, (S K K) x とやってみると,確かに x になる.この3番目の K は他に変えても, I のままである.例えば,(S K K) x の代わりに (S K I) x とやっても,結果は x になる.
このシステムは,コンビネータの式に名前をつけることができる.名前 exchange は, (S (K (S I))) K と定義してある.これも準備のところで述べた rxchange x y = y x を満たす コンビネータの式である.実際にやってみると期待通りの結果が得られる.
次は引数を2倍にする S I I を実行してみる.確かに (S I I) x = x x となっている. これを自分自身に適用すると,(S I I) = (S I I) = ... となり,無限ループに陥る. このシステムはこういう簡単なケースだけは Cycle detected とメッセージを出して止まるように している.
:l2c -d xxx = λ式
で与えられた式を SKI コンビネータの式に変換して結果を xxx に覚えておく.-d は, 変換の過程のトレースを表示するという意味である.これが無いと,結果だけが表示される. また,表示する文字は通常の ASCII キャラクタだけに限りたかったので, λx.E を x.E と表記してある.慣れるまで違和感があるかもしれないがご容赦いただきたい.
では,最初から少し高度なものを.x を x x に変える式を求めてみよう.これは ラムダ式で書くと,
λx.(x x)
である.我々の記法では,
x.(x x)
である.
SKI> :l2c -d xxx=x.(x x)
<- x.(x x) [ t(u.(A B)) = (S t(u.A) t(u.B)) ]
| <- x.x [ t(u.u) = I ]
| -> I [ t(u.u) = I ]
| <- x.x [ t(u.u) = I ]
| -> I [ t(u.u) = I ]
-> (S I) I [ t(u.(A B)) = (S t(u.A) t(u.B)) ]
=> (S I) I
"<-" は,その右辺の式が変換対象として入ってきたことを表している."->" は逆に 変換結果を表している.また,2行目の右側に表示されている
t(u.(A B)) = (S t(u.A) t(u.B))
は,変換したとき使ったルールを表している.ここで, t(...) は,... を SKI の式に変換するという意味である.つまり,このルールは
λu.(A, B) を (S t(λu.A) t(λu.B)) に変換する
というルールを表している.意味的には,A と B をそれぞれが引数を取れるように,λu.A と λu.B の 形にしてそれぞれ SKI の式に変換し,コンビネータ S を使って,変換結果の後ろに 引数が来た時,それぞれの SKI の式に分配するという式である.この例では λu は,λx で (A B) は (x x) だから,どちらも λx.x になり,その変換が3行目と5行目で要求されどちらも,4行目と6行目で I の結果を得ている.これらの部分式の変換を組み合わせて,最終的な答えが7行目に表示されている.結果は期待通り S I I となった.
次は,準備のところで説明した false に変換されるラムダ式を SKI の式に 変換してみる. false は
false x y = y
となる式でラムダ式で書くと(今後次第に,ツールに合わせてλを省略することが多くなってくる)
x.y.x (λx.λy.y を表す)
である.こちらは期待通り,K I になっている.λy.y には x は現れないので,λx.λy.y は, K を使って,K t(λy.y) とやればよい.つまり結果は K I である.
その後の,x.y.x は true = K に対応するλ式なのだが,変換のルール通りにやってしまうと, K が得られずに,かなり大きな式になる.一般にλ基の連鎖,λx.λy. は2重の変換を要求されるので 結果が大きくなりがちである.
SKI> :l2c -d xxx=x.y.y
<- x.y.y [ t(u.A) = K t(A) :when u not free in A ]
| <- y.y [ t(u.u) = I ]
| -> I [ t(u.u) = I ]
-> K I [ t(u.A) = K t(A) :when u not free in A ]
=> K I
SKI> :l2c -d xxx=x.y.x
<- x.y.x [ t(u.v.A) = t(u.t(v.A)) :when u free in v.A ]
| <- y.x [ t(u.A) = K t(A) :when u not free in A ]
| | <- x [ t(u) = u ]
| | -> x [ t(u) = u ]
| -> K x [ t(u.A) = K t(A) :when u not free in A ]
| <- x.(K x) [ t(u.(A B)) = (S t(u.A) t(u.B)) ]
| | <- x.K [ t(u.A) = K t(A) :when u not free in A ]
| | | <- K [ t(u) = u ]
| | | -> K [ t(u) = u ]
| | -> K K [ t(u.A) = K t(A) :when u not free in A ]
| | <- x.x [ t(u.u) = I ]
| | -> I [ t(u.u) = I ]
| -> (S (K K)) I [ t(u.(A B)) = (S t(u.A) t(u.B)) ]
-> (S (K K)) I [ t(u.v.A) = t(u.t(v.A)) :when u free in v.A ]
=> (S (K K)) I
次のは,2つの引数を交換する exchange だが,こちらも結果が
(S (K (S I))) ((S (K K)) I)
と,かなり大きくなっている. 準備の時に述べた exchange は,
(S (K (S I))) K
である.下の方の検算, xxx u v の評価を見ると,確かに v u とひっくり返された結果がでている.
SKI> :l2c -d xxx=x.y.(y x)
<- x.y.(y x) [ t(u.v.A) = t(u.t(v.A)) :when u free in v.A ]
| <- y.(y x) [ t(u.(A B)) = (S t(u.A) t(u.B)) ]
| | <- y.y [ t(u.u) = I ]
| | -> I [ t(u.u) = I ]
| | <- y.x [ t(u.A) = K t(A) :when u not free in A ]
| | | <- x [ t(u) = u ]
| | | -> x [ t(u) = u ]
| | -> K x [ t(u.A) = K t(A) :when u not free in A ]
| -> (S I) (K x) [ t(u.(A B)) = (S t(u.A) t(u.B)) ]
| <- x.((S I) (K x)) [ t(u.(A B)) = (S t(u.A) t(u.B)) ]
| | <- x.(S I) [ t(u.A) = K t(A) :when u not free in A ]
| | | <- S I [ t(A B) = t(A) t(B) ]
| | | | <- S [ t(u) = u ]
| | | | -> S [ t(u) = u ]
| | | | <- I [ t(u) = u ]
| | | | -> I [ t(u) = u ]
| | | -> S I [ t(A B) = t(A) t(B) ]
| | -> K (S I) [ t(u.A) = K t(A) :when u not free in A ]
| | <- x.(K x) [ t(u.(A B)) = (S t(u.A) t(u.B)) ]
| | | <- x.K [ t(u.A) = K t(A) :when u not free in A ]
| | | | <- K [ t(u) = u ]
| | | | -> K [ t(u) = u ]
| | | -> K K [ t(u.A) = K t(A) :when u not free in A ]
| | | <- x.x [ t(u.u) = I ]
| | | -> I [ t(u.u) = I ]
| | -> (S (K K)) I [ t(u.(A B)) = (S t(u.A) t(u.B)) ]
| -> (S (K (S I))) ((S (K K)) I) [ t(u.(A B)) = (S t(u.A) t(u.B)) ]
-> (S (K (S I))) ((S (K K)) I) [ t(u.v.A) = t(u.t(v.A)) :when u free in v.A ]
=> (S (K (S I))) ((S (K K)) I)
SKI> xxx u v
=> (((S (K (S I))) ((S (K K)) I)) u) v
=> (((K (S I)) u) (((S (K K)) I) u)) v
=> ((S I) (((K K) u) (I u))) v
=> (I v) ((((K K) u) (I u)) v)
=> v ((K u) v)
=> v u
最後に,Y コンビネータ,
Y = λf.((λx.(f (x x))) (λx.(f (x x))))
の SKI コンビネータ式を求めてみる.結果は結構大きな式になる. こちらは Y g を評価すると
Y g => g (Y g) => g (g (Y g)) => ...
と止まらなくなってしまうはずである.一応,変換回数に制限を設けているので, 次のログでは50回目に諦めてとまっている.その間,g を前にいくつもつけるような動作を 行っている.
SKI> :l2c Y=f.((x.(f (x x))) (x.(f (x x))))
=> (S ((S ((S (K S)) ((S (K K)) I))) (K ((S I) I)))) ((S ((S (K S))
((S (K K)) I))) (K ((S I) I)))
SKI> Y g
=> ((S ((S ((S (K S)) ((S (K K)) I))) (K ((S I) I)))) ((S ((S (K S))
((S (K K)) I))) (K ((S I) I)))) g
=> (((S ((S (K S)) ((S (K K)) I))) (K ((S I) I))) g) (((S ((S (K S))
((S (K K)) I))) (K ((S I) I))) g)
=> ((((S (K S)) ((S (K K)) I)) g) ((K ((S I) I)) g)) ((((S (K S))
((S (K K)) I)) g) ((K ((S I) I)) g))
=> ((((K S) g) (((S (K K)) I) g)) ((S I) I)) ((((K S) g)
(((S (K K)) I) g)) ((S I) I))
=> ((S (((K K) g) (I g))) ((S I) I)) ((S (((K K) g) (I g))) ((S I) I))
=> ((((K K) g) (I g)) ((S (((K K) g) (I g))) ((S I) I))) (((S I) I)
((S (((K K) g) (I g))) ((S I) I)))
=> ((K g) ((S (K g)) ((S I) I))) ((I ((S (((K K) g) (I g))) ((S I) I)))
(I ((S (((K K) g) (I g))) ((S I) I))))
=> g (((S (((K K) g) (I g))) ((S I) I)) ((S (((K K) g) (I g))) ((S I) I)))
=> g (((((K K) g) (I g)) ((S (((K K) g) (I g))) ((S I) I))) (((S I) I)
((S (((K K) g) (I g))) ((S I) I))))
=> g (((K g) ((S (K g)) ((S I) I))) ((I ((S (((K K) g) (I g))) ((S I) I)))
(I ((S (((K K) g) (I g))) ((S I) I)))))
=> g (g (((S (((K K) g) (I g))) ((S I) I)) ((S (((K K) g) (I g))) ((S I) I))))
...
=> g (g (g (g (g (g (g (g (g (g (g (g (g (g (g (((S (((K K) g) (I g)))
((S I) I)) ((S (((K K) g) (I g))) ((S I) I)))))))))))))))))
*** Limit(50) exceeded
変換の例ではないが,このインタープリタは SKI のほかに組み込みのコンビネータとして 次のようなものを持っている.
SKI> :r Rules for system combinators ------------------------------------- 1. (I x) => x 2. ((K x) y) => x 3. (((S x) y) z) => ((x z) (y z)) 4. (((C f) x) y) => ((f y) x) 5. (((B f) g) x) => (f (g x)) 6. (M x) => (x x) 7. ((T x) y) => (y x) 8. (((R x) y) z) => ((y z) x) 9. (((V x) y) z) => ((z x) y) 10. ((W x) y) => ((x y) y) 11. (X x) => ((x S) K) 12. (Y0 f) => (f (Y0 f)) 13. ((Z g) v) => ((g (Z g)) v)
Y0 や Z は不動点コンビネータである.
また,予めいくつかのコンビネータの式に名前をつけている. 次の Y10 や Y2 は,不動点コンビネータの機能を持っているものだが, 自動でラムダ式 Y から変換したものに比べてずいぶん短い.
SKI> :ls Current definitions ------------------------------------- 1. exchange = S (K (S I)) K 2. demo = exchange x y 3. sii = S I I 4. omega = sii 5. aa = omega a 6. Omega = omega omega 7. Y10 = S (K (S I I)) (S (S (K S) K) (K (S I I))) 8. Y2 = S S K (S (K (S S (S (S S K)))) K) 9. true = K 10. false = K I 11. not = V false true 12. and = R false 13. or = T true 14. imply = T true 15. equiv = C S not 16. zero = I 17. suc = V false 18. eq_zero = T true 19. pre = T false 20. test1 = eq_zero (pre (suc zero)) 21. test2 = eq_zero (suc zero)
確かに, Y10 g とやると
SKI> Y10 g
=> ((S (K ((S I) I))) ((S ((S (K S)) K)) (K ((S I) I)))) g
=> ((K ((S I) I)) g) (((S ((S (K S)) K)) (K ((S I) I))) g)
=> ((S I) I) ((((S (K S)) K) g) ((K ((S I) I)) g))
=> (I ((((S (K S)) K) g) ((K ((S I) I)) g))) (I ((((S (K S)) K) g) ((K ((S I) I)) g)))
=> ((((S (K S)) K) g) ((K ((S I) I)) g)) ((((S (K S)) K) g) ((K ((S I) I)) g))
=> ((((K S) g) (K g)) ((S I) I)) ((((K S) g) (K g)) ((S I) I))
=> ((S (K g)) ((S I) I)) ((S (K g)) ((S I) I))
=> ((K g) ((S (K g)) ((S I) I))) (((S I) I) ((S (K g)) ((S I) I)))
=> g ((I ((S (K g)) ((S I) I))) (I ((S (K g)) ((S I) I))))
=> g (((S (K g)) ((S I) I)) ((S (K g)) ((S I) I)))
=> g (((K g) ((S (K g)) ((S I) I))) (((S I) I) ((S (K g)) ((S I) I))))
=> g (g ((I ((S (K g)) ((S I) I))) (I ((S (K g)) ((S I) I)))))
=> g (g (((S (K g)) ((S I) I)) ((S (K g)) ((S I) I))))
=> g (g (((K g) ((S (K g)) ((S I) I))) (((S I) I) ((S (K g)) ((S I) I)))))
=> g (g (g ((I ((S (K g)) ((S I) I))) (I ((S (K g)) ((S I) I))))))
=> g (g (g (((S (K g)) ((S I) I)) ((S (K g)) ((S I) I)))))
=> g (g (g (((K g) ((S (K g)) ((S I) I))) (((S I) I) ((S (K g)) ((S I) I))))))
...
*** Limit(50) exceeded
と,g を次々に前に付けていく動作を行う.
今回は,SKI のインタープリタとλ式から SKI コンビネータ式への変換ツールを Ruby で 書いてみた.
コンビネータの式は簡単な機能のものでもすぐ大きくなっていくので実行や変換を 追って行っても,サイズが大きくなるとすぐ人間の理解の限界を超えてしまう. たぶん,自分でこういうツールを作ってみるのがよい勉強になるんだろうなと思った. 今回のプログラムは Ruby で空行やコメントも入れて,668 行である.お勉強を兼ねて 作ってみるのに手ごろな大きさである.
論理学,集合論など,数学基礎論っぽいテーマはここにもたくさん書いてあり,
私はよく活用させていただいている.
λ計算とコンビネータ論理の両方を含むテキストとしては次のようなものがある.
#include <stdio.h> int fact(int n, int (*g )()) { if (n == 0) return 1; else return n*(*g )(n-1,g ); } int main(void) { int ret; ret =fact(10, fact) ; /* gにfactをバインディング */ printf("fact(10) = %d\n", ret); return 0; }
:help とやると,全機能がリストアップされる.この中で,:let コマンドは コンビネータの式に名前をつける機能で少しずつ複雑な式を定義していくとき 便利である.:l2c (lambda expression to combinator expression)は,本文の 中でも述べたように,λ式をコンビネータの式に変換するコマンドであり, 変換過程をトレースできるようになっている.
本文では紹介しなかった
SKI> :help
Commands
--------------------------------------------------
:let ... :let <NAME> = <COMBINATOR EXPRESSION>
sets <COMBINATOR EXPRESSION> to <NAME>
:list ... shows <NAME>s currently defined
:del ... :del <NAME>
deletes the definition of <NAME>
:clear ... clears all <NAME>s
:l2c ... :l2c [-d] <NAME> = <LAMBDA TERM>
converts <LAMBDA TERM> to an expression of S, K, I and
sets it to <NAME>. Write x.E for Lx.E where L means lambda.
Lx is right associative while applications are left
associative, e.g., x.y.(x y x) means Lx.(Ly.((x y) x))
-d shows the process of the translation.
:limit ... :limit [N]
sets limit to stop infinite loop (default=50)
:pp ... toggles pretty print mode (default = false).
:rule ... shows the rules for system combinators S, K, I, ...
:load ... :load <FILE>
change input from spefified <FILE>.
:pause ... :pause some message
waits for hitting Enter key.
:help ... shows this message
:quit ... quits SKI Interpreter
Expression beginning with a character other than ':' is evaluated
as a combinator expression. When you omit parentheses, expressions
are combined left to right, for example, T1 T2 T3 T4 is interpreted
as (((T1 T2) T3) T4). You can use <NAME> as a part of input.
<NAME>s are replaced by the strings you set to them.
プリティプリントモードは通常 false になっているが,これをtrue にすることにより, コンビネータの式を計算する過程が簡易ツリー表示されるようになっている.
次のログでは最初に :pp でプリティプリントモードに入り,二つの引数を交換する コンビネータの式 exchange = (S K (S I))) K を表示している.自分の経験だが, 最初にコンビネータの式を見たときは,括弧だけでは,それがどのような構造をしているのか イメージしにくかった.ここでの簡易ツリー表示は左が木(ツリー)の根で右が葉っぱで ある.(S (K (S I))) K は根の最初の子供が (S (K (S I))) で,二番目の子供が K と 読む.コンビネータの式は二分木である.
SKI> :pp
pp mode is set to true
SKI> exchange
=> (S (K (S I))) K
+--+--S
| `--+--K
| `--+--S
| `--I
`--K
SKI> exchange x y
=> (((S (K (S I))) K) x) y
+--+--+--+--S
| | | `--+--K
| | | `--+--S
| | | `--I
| | `--K
| `--x
`--y
=> (((K (S I)) x) (K x)) y
+--+--+--+--K
| | | `--+--S
| | | `--I
| | `--x
| `--+--K
| `--x
`--y
=> ((S I) (K x)) y
+--+--+--S
| | `--I
| `--+--K
| `--x
`--y
=> (I y) ((K x) y)
+--+--I
| `--y
`--+--+--K
| `--x
`--y
=> y x
+--y
`--x
一応,主要なコンビネータの式を簡易ツリー表示しておこう.以下では,SKI 以外の コンビネータも出てくるので,ここでの定義をまず列挙しておく.
Rules for system combinators ------------------------------------- 1. (I x) => x 2. ((K x) y) => x 3. (((S x) y) z) => ((x z) (y z)) 4. (((C f) x) y) => ((f y) x) 5. (((B f) g) x) => (f (g x)) 6. (M x) => (x x) 7. ((T x) y) => (y x) 8. (((R x) y) z) => ((y z) x) 9. (((V x) y) z) => ((z x) y) 10. ((W x) y) => ((x y) y) 11. (X x) => ((x S) K) 12. (Y0 f) => (f (Y0 f)) 13. ((Z g) v) => ((g (Z g)) v)
これらの定義のもとに,いくつかのコンビネータの式の簡易ツリー表示や 計算過程を示す.
SKI> true
=> K
K
SKI> false
=> K I
+--K
`--I
SKI> not
=> (V (K I)) K
+--+--V
| `--+--K
| `--I
`--K
SKI> not true
=> ((V (K I)) K) K
+--+--+--V
| | `--+--K
| | `--I
| `--K
`--K
=> (K (K I)) K
+--+--K
| `--+--K
| `--I
`--K
=> K I
+--K
`--I
SKI> or
=> T K
+--T
`--K
SKI> or false true
=> ((T K) (K I)) K
+--+--+--T
| | `--K
| `--+--K
| `--I
`--K
=> ((K I) K) K
+--+--+--K
| | `--I
| `--K
`--K
=> I K
+--I
`--K
=> K
K
SKI> sii sii
=> ((S I) I) ((S I) I)
+--+--+--S
| | `--I
| `--I
`--+--+--S
| `--I
`--I
=> (I ((S I) I)) (I ((S I) I))
+--+--I
| `--+--+--S
| | `--I
| `--I
`--+--I
`--+--+--S
| `--I
`--I
=> ((S I) I) ((S I) I)
+--+--+--S
| | `--I
| `--I
`--+--+--S
| `--I
`--I
計算機(主にソフトウェア)の話題 へ
圏論を勉強しよう へ
束論を勉強しよう へ
半群論を勉強しよう へ
ホームページトップ(Top of My Homepage)