
私は圏論の初心者用の入門資料を整備しようとしていて,とりあえず,1つ
計算機科学のための圏論の基礎の基礎 (2020年 3 月)を作成しました.しかし,この資料ではまだ
一応,Awodey は,それらの数学的概念については,その本の中できちんと説明してくれてはいるのです.
例えば,ブール代数は第2章で,ハイティング代数は第6章で説明しています.しかし,
やはり,必要な概念,しかもある程度高度な概念を
そこで,ここではそれら(ブール代数など)について,できるだけ分かりやすくまとめて,
と言うことで,ここでは,それらの概念について,できるだけ分かりやすく,
以下,時々,用語が英語だけのことがあります.これは私が適切な訳語を知らないことが 多いためで,申し訳ありません.訳語が分かったら,適宜,修正するようには努力します.
追記:
ブール代数やハイティング代数の利用法としては,記号論理に意味を与えると言う用法が
代表的なものなので,最初の項目として
形式的論理体系の定義からレーベンハイム・スコーレムの 定理までの大急ぎのまとめにある程度書きましたので,ご興味のある方は参照してください.
命題論理に関して,
[ 計算機科学向け 圏論の基礎 ] デカルト閉圏の学習に向けて
命題論理とその解釈のための代数系の基礎知識 (PDF)命題論理(古典,直観主義),
順序集合,
半束,束,Heyting 代数,Bool 代数なお,この解説動画が Youtube にあります.
命題論理とその解釈のための代数系の基礎知識 (Youtube 動画)2023.04.11
命題論理 (Propositional logics)
2021.04.01この項目の内容
はじめに ブール代数やハイティング代数の用途の代表的なものとしては形式論理に意味を与えると いうことがあると思います.
そのような例を説明するためにはある程度,形式論理の知識が なければなりません.この項目でも,そのような知識として最小限度,命題論理に限って 必要なことを記述しておきます.もし,述語論理についても興味があるという方が いらっしゃいましたら,述語論理の体系の説明は ,以前,
形式的論理体系の定義からレーベンハイム・スコーレムの 定理までのにある程度書きましたので,そちらをご参照ください.
大急ぎのまとめ命題論理は,一つの命題が最小の構成要素となる記号論理です.命題とは真か偽が定まるような記述で,例えば,x2+y2=1 のようなものですが,命題論理で扱う命題ではその中身の構造は気にしません.つまり,x2+y2=1 では,変数 x, y や + などの記号やそのつながりは気にせず,全体として「x2+y2=1」という 一つの命題があるという具合に認識します.それに対して,上で述べた述語論理では,この中身の構造まで意識します.
以下,次の項目では命題論理を記述するための枠組みを述べます.これは,命題論理の命題記号や それらの命題をつなぎ合わせてより大きな命題を構成する手段のことです.
次にその枠組みを使って,2つの命題論理,古典命題論理と直観主義命題論理について記述します.
命題論理を規定する枠組み 命題論理は,
命題論理の言語 L
どのような文字列が命題として扱われるのかを規定する.
命題論理の公理と推論規則
命題として規定されたものの中で正しい命題を導き出すための 道具立てを規定する.
の2つにより規定されます(下図参照.図では,公理と推論規則は別々に書いています).
ここではこれらについて説明します.
まず,命題論理を記述するための言語について説明します. 言語規定するための道具立てとしては次のものが定められます.
命題論理の言語の枠組み
命題を表す定数記号の集合
なにか決まった内容の命題を表す記号の集合.これを定める人は 何か意図を持っている訳ですが,言語の枠組みとしては単に記号の 集合です.それらの記号の中に真を表す true と偽を表す false が良くつかわれることがあります. true は⊤ , false は⊥ と 書くこともあります.
命題を表す変数記号の集合
なにか不特定の命題を表す記号の集合です.p, q, r, ... などで表されます.ここでは, そのような記号が可算無限個(自然数と同じだけ)用意されているとします.
(1個以上の)命題から新しい命題を作る論理記号の集合
否定を表す ¬ や「または」を表す ∨ や「かつ」を表す ∧, 「ならば」を表す → などです.それぞれの記号には何個の命題を 結合して新たな命題を作るかが決められています.その個数のことをarity と言います.次のような論理記号がよく使われます.
¬ : arity=1, 意図としては否定を表す
¬p
∨ : arity=2, 意図としては「または」を表す
p∨q
∧ : arity=2, 意図としては「かつ」を表す
p∧q
→ : arity=2, 意図としては「ならば」を表す
p→q
↔ : arity=2, 意図としては「同値」を表す
p↔q
その他にも用途に応じて,色々な記号を用意することがあります. 例えば,
「必ず起こる □」などのような, いわゆる「様相」を表すような記号を使う場合もあります.「起こる可能性がある ◇」
カッコ
曖昧性を解消するために適宜カッコを使うこともあります. 厳密に言えば,上の論理記号の導入のときに,p∨q でなく (p∨q) あるいは(p)∨(q) のようにカッコで曖昧性が無いような 文法を導入することが必要なのですが,読みにくいので, ここでは適宜省略します.
上のように,定数記号の集合,変数記号の集合,論理記号の集合を定めると それらの組合せとして,命題論理で表現される「命題」の集合が規定される訳ですが,さらに,次のようにして この上に推論の機構が定義されます.
命題論理の上の推論の機構 これは規定されようとしている命題論理において,「正しい」命題とは 何かを規定する枠組みです.この枠組みは正しい命題である
公理の集合 と,すでに正しいと分かっている命題から新たな正しい命題を導出するための推論規則の集合 からなります.
公理の集合
その論理の言語で規定された命題の集合のうち,ある命題の集合を公理として 設定します.このような公理の集合は通常無限集合になります.例えば, 普通は,命題変数 p に対して,p→p は公理ですが,この命題単独でなく, p の所に,例えば,q∨r を入れた,(p∨r)%rarr;(p∨r) も公理として 入れる必要がある場合が多々あります.このような同じ型の命題を公理として指定する方法として,
「公理スキーム」 による公理の指定方法があります. それは,公理1つ1つを指定するのではなく,どんな命題が入っても良い 変数を用意して,一気に沢山の命題を公理として指定する方法です. 例えば,A と B をそのような,任意の命題を表す変数として,A→Aは公理ですよというように公理を指定します.この1つ目の命題は単一の命題を表している 訳ではなく,A に文法的に正しいどんな命題を入れた場合も これが公理であると言っている訳です.2番目の式も,A と B にそれぞれ あらゆる可能な命題を入れて出来たものはすべて公理であるということを 言っています.このような指定を「公理スキーム」と呼びます.や
A→(B→A)
推論規則の集合
これは,すでに正しいと分かっている命題から,正しい命題を導出するための 規則です.代表的なものはモーダス・ポーネンス (modus ponens )と呼ばれるA A→Bのような推論規則です.これは,A という命題と,A→B という命題が正しいと 分かっているときは,B という命題を正しいとして良いということを 表しています.モーダス・ポーネンスは
--------------
B三段論法 とも呼ばれます.
命題論理の記述体系には色々なものがあります.例えば,ヒルベルトの体系(Hilbert-style system),ゲンツェンの自然演繹法(Genzen's NK )などです. ヒルベルトの体系とゲンツェンの自然演繹法は公理と推論規則の重みが異なっています. ヒルベルトの体系では多量の公理と少数の推論規則(通常,モーダスポーネンス1つだけ)を使うのに 対して,ゲンツェンの自然演繹法では,少量の公理と多くの推論規則を使います. このページでは基本的にヒルベルトの流儀で行きます.
このページではいくつかの具体的な命題論理体系を述べますが,それらの具体的な言語,公理, 推論規則はそこで述べます.
また,論理体系は非常に多くが提案されており,中にはここで述べた枠組みに収まらないものもあります.
この枠組みの項目の最後に,命題論理の証明系の用語をいくつか定義しておきます.
証明系の用語の定義
導出関係
PSet を命題の集合,P を命題とする.このとき,PSet が P を導出する とは,有限個の命題の列P0, P0, P1, ..., Pnが存在し,Pn=P であり,また,i≤n に対して Pi がときにいう.PSet が P を導出することを記号で
- 公理であるか,あるいは
- 命題の集合 PSet に属しているか,あるいは
- Pj j<i に現れるどれかの命題の集合から推論規則を使って得られたものである
PSet ⊦ Pと表す.また,上の命題の列P0, P0, P1, ..., Pnを PSet から P の導出列 と言う.証明
P を命題とするとき,公理の集合 Axioms から P の導出列を P の証明 という.このとき,Axioms を省略して,記号で,⊦ Pと書く.
定理
⊦ P となるとき,P は定理 であるという.
命題論理の意味論的な特徴づけ(1) - 健全性と完全性 前の項目までで,命題論理について
言語 (命題定数,命題変数,論理記号)推論機構 (公理と推論規則)導出,証明,定理 の概念が導入されました.これらはいわゆる
「証明論」 の立場からの命題論理の枠組みです. つまり,予め正しいと定めた「公理」の集合から次々に「証明」により, 正しいと認められる「定理」を導出する仕掛けです.命題論理には,もう一つの立場,
「意味論」 の立場からの枠組みがあります.このページの主題であるブール代数やハイティング代数は命題論理で記述される色々な 命題の表現に「意味」としてそれらの代数のなんらかの値を割り当てるために 使われます.ここではごく小さなブール代数
2 := {0, 1} を使って, 命題論理に意味を与えるとはどういうことかを説明して,それに関するいくつかの 概念や性質を述べておきます.これらについては,後の項目「命題論理の意味論的な特徴づけ(2)- 一般的な枠組みでの定義 - 」で,より本格的に定義しています.こちら側では,命題論理の「意味論的なアプローチ」に 慣れるという意味で限定的に,かつ,平易に説明しています.すでに「意味論」という概念に慣れる必要は ないという方は,ここは飛ばしても結構です.いま,説明のための例用の命題論理の言語 L を考えます.
説明用の小さな言語 L
- 命題定数は {true, false}
- 可算無限個の命題変数 PVars := {p, q, r, ...} が用意されている
- 論理記号としては ∨, ¬ だけがある.ただし,∧ と → は 次のような内容の命題の省略形として用いる.
p ∧ q := ¬(¬p ∨ ¬ q)
p → q := ¬p ∨ qこの言語で記述された命題の集合を L と書くことにします.
今,PVars から
2 := {0, 1} への関数 m があったとします.m : PVars → {0, 1}このような m を変数への値の割り当て と呼ぶことにします.このとき,次のように再帰的に m を L → {0, 1} の関数に拡張します. この拡張された関数も m で表すことにします.
m : PVars→{0, 1} の m : L → {0, 1} への拡張
m(true) = 1
m(false) = 0;
m(p) = m(p) if p∈PVars ただし,右辺の m は m : PVars→{0, 1} の m
m(p ∨ q) = m(p) ∨ m(q)
m(¬p) = ¬m(p)
(注意)左辺に現れる ∨ や ¬ は単なる記号で,右辺の ∨ や ¬ は {0, 1} 上の論理演算であることに注意してください.
このように m : L → 2 を定義すると,命題の集合
を定義することができます.これは m : PVars→{0, 1} の割り当てで 真になる命題の集合です.また,どんな m : PVars→{0, 1} に対しても 真になる命題の集合も定義できます.valid(L, m) := {p∈L | m(p) = 1}p∈valid(L) のことをvalid(L) := {p∈L | m(p) = 1 for ∀ m : PVars→{0, 1}}とも書きます.⊧ p Props⊆L とし,p∈L とします.このとき,Props の命題を真にする どのような割り当て m : PVars→{0, 1} でも m(p)=1 になるなら,
と書きます.Props ⊧ p 以上で,命題論理について
「正しい」 命題を分別する2つの方法が得た得られた訳です. つまり,
- 証明論的な方法
⊦ p - 意味論的な方法
⊧ p これら2つの方法で得られた「正しい」命題の集合の間の重要な関係として,
健全(sound) と完全(complete) が あります.この項目では,これらを説明して終わります.
命題論理体系の健全性と完全性 Σ を命題論理の体系とする. Σ では,命題を記述するための言語 L, 公理 Axioms,推論規則 Rules が規定されている.このとき,「健全」,「完全」の 概念を次のように定義する.
- Σ が
健全(sound) であるとは,命題論理 Σ の体系で 導出される定理 T は意味論の観点で正しいこと,すなわち,モデル m に対しても,m(T)= 1になることとする.つまり,⊦T ならば ⊧ T
- Σ が
完全(complete) であるとは,意味論の観点で正しい 命題はすべて,定理になること.つまり⊧ T ならば ⊦T
(「充足可能性(satisfiable)」,「モデル」も追加すること)
古典命題論理 この資料では古典命題論理と直観主義命題論理を命題論理の具体例として書いておきます. まず,この項目では古典命題論理を記述します.古典命題論理は,排中律と呼ばれる
P ∨ ¬ Pの形式の命題が成立することが特徴です.古典命題論理も直観主義命題論理も命題論理の体系は色々な記述方法があります.ここでは, その1つの記述方法だけを述べます.
古典命題論理の言語は次の通りとします.
- 命題記号: なし
- 命題変数: p, q, r, ... など可算無限個の変数が用意されているとする
- 論理記号: ∨, ∧, ¬, →
公理は次の通りとします.ここで,A, B, C は命題変数でなく,どんな命題が入っても良い,いわばメタな変数です.実際は,それらのメタ変数に任意の命題を入れたものが公理になります.したがって,次の表は11個の公理に見えますが,無数の公理を表しています. このようなメタな変数を含んだ公理の集合を記述するものを
公理スキーム(axiom scheme) と言います.命題論理の公理は通常,このような 公理スキームで表されます.
名称 公理スキーム THEN-1 A → (B→A) THEN-2 (A → (B→C)) → ((A→B) → (A→C)) AND-1 (A∧B) → A AND-2 (A∧B) → B AND-3 A → (B → (A∧B)) OR-1 A → (A∨B) OR-2 B → (A∨B) OR-3 (A→C) → ((B→C) → ((A∨B) → C)) NOT-1 (A→B) → ((A → (¬B)) → (¬A)) NOT-2 A → ((¬A) → C) NOT-3 A ∨ (¬A) 何か良く分からない命題が沢山ありますね.この中で最初の2つ,
THEN-1 と THEN-2 が特に重要 です.また,「古典」 命題論理という意味では,NOT-3 A∨(¬A) も重要です. これは「排中律( Law of excluded middle)」 と呼ばれます.名前から言うと, 真と偽の中間的な状態が無いと言うことですね.THEN-1 と THEN-2 が重要なのは, もともと,古典論理は,「ならば(→)」と真偽値 true, false があれば記述できるからです. THEN-1 と THEN-2 は,この「ならば(→)」を特徴づけています.他の公理は,それぞれの 論理記号の意味を記述しています.推論規則はモーダス・ポーネンスだけです.
A A→B
----------------
Bこのシステムでの証明は,結構大変です.例えば,p を命題変数としたとき,p→p は 証明できて欲しいので,証明してみましょう.
p→p の証明
[1] (p → ((p→p)→p)) → ((p→(p→p)) → (p→p))公理 THEN-2: (A → (B→C)) → ((A→B) → (A→C))
で A := p, B := p→p, C := p
[2] (p → ((p→p)→p))
公理 THEN-1: A → (B→A)
で A := p, B := p→p
[3] (p→(p→p)) → (p→p)
[2] と [1] からモーダス・ポーネンス
[4] (p→(p→p))
公理 THEN-1 で A := p, B := p
[5] p→p
[4] と [3] からモーダス・ポーネンス
「よくこんな証明を思いつくな~」と思うでしょう.また,「公理系もどうやって選んでいるんだろう?」と思うでしょう. 公理はアドホックに選んでいる訳でなく,考えて選んでいるみたいです.
とりあえず,証明のヒントだけ説明しておきましょう.
この命題論理の体系は次の性質を持っています.
演繹定理(deduction theorem) PSet を命題の集合,P と Q を命題とする.このとき次の関係が成り立つ.
PSet ∪ {P} ⊦ Q ⇔ PSet ⊦ P→Qつまり,
PSet から P→Q が証明できるのは,PSet と P を合わせて, Q が証明できるのと同じだということです.何を当たり前のことを言っているんだと思うかもしれませんが, これは当たり前ではありません.我々の論理ではそうなりますが,ここでは命題論理は 公理と推論規則を決めて作ったわけで,その作り方が,我々の論理を正しく 反映しているとは限らないからです.つまり,この定理が言っていることは,上で 選んだ公理と,推論規則のモーダス・ポーネンスは正しく,我々の論理を表現できている ということです.この定理の右から左を出すのは簡単です.
PSet ⊦ P→Q なら,PSet ∪ {P} ⊦ P→Q かつ
PSet ∪ {P} ⊦ P
ですから,P と P→Q からモーダス・ポーネンスを使って,
PSet ∪ {P} ⊦ Q
が証明されます.
逆が少し難しいです.これには数学的帰納法を使い,PSet ∪ {P} ⊦ Q の証明から PSet ⊦ P→Q の証明を構成します.
ということは,
訳です.あれ? 上と同じことを言ってしまいました.まあ,重要なことなので 二回言っても良いでしょう.PSet ∪ {P} から Q が証明できれば,その証明から PSet ⊦ P→Q の証明が構成できる ということは,命題変数と → だけ使ってできた命題 P の証明は次の疑似コードで 書いたようなアルゴリズムで出来ると言うことです.
algorithmProve (P) /* 命題変数と → だけで出来た命題 P を受け取り, 証明できればその証明を返し,証明できなければ fail を返す */ beginProve2 ({}, P); end
algorithmProve2 (PSet, P) /* 命題の集合 PSet を仮定した P の証明を返す. 証明できなければ fail を返す */ begin if (Pが公理 または P∈PSet) then return [P]; else if (P が Q→R の形) then proof =Prove2 (PSet∪{Q}, R); if (proof != fail) then proof を加工して Q→R の証明にして返す; (これは演繹定理から可能) else return fail; end else return fail;(ここですぐ fail ではダメでした.例えば, (a→b)→c と a→b から c が導けません. 再考,再調査します.すみませんでした. 2021.07.16) end end一応,演繹定理も証明しておきましょう.これが,PSet∪{P} ⊦ Q の証明を 加工して PSet ⊦ P→Q の証明にする方法を与える訳ですから, 特に,自動的な証明の生成アルゴリズムに興味のあるような人は,良く内容を 見ておいてください.
演繹定理の証明 演繹定理: PSet∪{P} ⊦ Q ならば PSet ⊦ P→Q
[証明] PSet∪{P} ⊦ Q の証明の長さ n に関する数学的帰納法で証明する.
n=1 の場合
次の場合があり,それぞれ PSet ⊦ P→Q の証明に再構成できる.
Q が公理 または Q∈PSet 公理 THEN-1 Q→(P→Q) と Q からモーダス・ポーネンスを 使って,P→Q の証明を得る
Q=P P→Q は Q→Q だから,先に書いた p→p の証明と 同様に,PSet の内容に関わらず,証明される
n=k+1 の場合
証明の長さが k 以下のPSet∪{P} ⊦ Q の証明は PSet ⊦ P→Q の証明に再構成できるとする.次のような場合があり,それぞれ PSet∪{P} ⊦ Q の証明を PSet ⊦ P→Q の証明に再構成できる.
従って,(H1), (H2), (1), (2), (3) により PSet ⊦ P→Q の証明が得られる.
Q が公理,または,Q∈PSet または Q=P n=1 の場合と同様.
何かある命題 S があり S S→Qで Q が得られた場合
------------------
Qこの場合,
PSet∪{P} ⊦ Sであり,これらの証明の長さは n 以下であるから,
PSet∪{P} ⊦ S→Q
(H1) PSet ⊦ P→Sの証明がある.これらから,以下のように THEN-1 と THEN-2 を 使って,P→Q が証明される.
(H2) PSet ⊦ P→(S→Q)
(1) (P→(S→Q))→((P→S)→(P→Q))公理 THEN-2 (A→(B→C))→((A→B)→(A→C))
(2) (P→S)→(P→Q)
(H2) と (1) からモーダス・ポーネンス
(3) P→Q
(H1) と (2) からモーダス・ポーネンス
[証明終り]
直観主義命題論理 これは排中律 P∨(¬P) が必ずしも成り立つとは限らない命題論理です.
言語は次の通りとします.
- 命題記号: なし
- 命題変数: p, q, r, ... など可算無限個の変数が用意されているとする
- 論理記号: ∨, ∧, ¬, →
公理スキームは次の通りとします.古典論理と殆ど同じです.最後の排中律 NOT-3 が 無いだけです.THEN-1 と THEN-2 は同じですから,→ に関して演繹定理は成り立ちます.
名称 公理スキーム THEN-1 A → (B→A) THEN-2 (A → (B→C)) → ((A→B) → (A→C)) AND-1 (A∧B) → A AND-2 (A∧B) → B AND-3 A → (B → (A∧B)) OR-1 A → (A∨B) OR-2 B → (A∨B) OR-3 (A→C) → ((B→C) → ((A∨B) → C)) NOT-1 (A→B) → ((A → (¬B)) → (¬A)) NOT-2 A → ((¬A) → C) NOT-3A ∨ (¬A)この命題論理体系は,このページの後ろの方で紹介しているハイティング代数(Heyting algebras) がモデルになります.
命題論理の意味論的な特徴づけ(2)- 一般的な枠組みでの定義 - 先に,「命題論理の意味論的な特徴づけ(1) - 健全性と完全性」 で命題論理の意味論について,命題を {0, 1} で解釈する意味論に ついて述べました.しかし,直観主義命題論理を解釈する場合などは,{0, 1} だけの真偽値で 解釈するのではなく,多値で命題の真偽性を解釈するようなことが必要になってきます.そこで, ここでは
- より一般的な意味論の枠組みの記述
- その上での,「解釈」,「モデル」,「充足可能性」,「健全性」,「完全性」などの概念の導入
- それらと,証明論での「証明可能性」などとの関係の記述
を行っておきます.
命題論理の
言語 L と推論機構 が次のように与えられているとします.
言語 L : 次の記号を使って生成される命題の集合これらが決まれば,正しい形の命題の集合 L が定まる.このような与えられた 文法に従った命題のことを
- 命題定数の集合
Consts - 命題変数の集合
PVars - 論理記号の集合
LSymbols
各論理記号に対しては,引数としてとる命題の個数(arity)が 決まっているものとし,また,本来は文法をきちんと述べるべきだが, 論理記号の繋がり方を明確にするための括弧は適宜使えるものとする.well-formed formulae (略してwff )と呼ばれることもある(formulae は formula の 複数形).
推論機構
- 公理
Axioms ⊆L- 推論規則
Rules
- 解釈
- モデル
- 充足可能性
- 充足不可能
- 証明可能
- 正しい(valid)
- 健全性
- 完全性
(そのうち)
古典命題論理と直観主義命題論理の関係 2021.07.15 (木)ここでは証明など深い議論は避けるが,古典命題論理と直観主義命題論理の間には 次の2つの一見相反する内容に見える「微妙な」関係があります.
直観主義論理は真に(strict に)古典命題論理より弱い 古典命題論理では証明できるが直観主義命題論理では証明できない命題が 存在します.代表的なものは
P ∨ ¬Pなどです.これらが証明できないことは,このページの最後の方で述べる ハイティング代数による解釈を使うと楽に証明することができます.
¬¬P → P
¬(P ∧ Q) → (¬P ∨ ¬Q)一方,上の命題と似ていますが,次の命題は証明できます.
¬P ∨ ¬¬P
P → ¬¬P
(¬P ∨ ¬Q) → ¬(P ∧ Q)
古典命題論理は直観主義命題論理の中に埋め込むことができる 古典命題論理の命題 P に対して,
上の図のように,Gödel-Genzen double negation transformation と呼ばれる直観主義命題論理の命題gg(P) を割り当てて,とすることができます.例えば,P が古典命題論理で証明可能 ⇔gg(P) が直観主義命題論理で証明可能 ということになります. また,これは,述語論理に拡張しても,∀ と ∃ の変換をうまく定義することで成り立ちます.ここでは,この証明には 立ち入りませんが,このページの後ろの方にある 「ハイティング代数」の ところの「ハイティング代数の中のブール代数」という項目に, 直観主義命題論理の解釈となるハイティング代数の中に 二重否定の関数でブール代数になる部分代数がとれることを書いておきました. この二つのことは密接に関係しています.P→Q が古典命題論理で証明可能 ⇔¬¬P→¬¬Q が直観主義論理で証明可能
含意(→)の公理と SK コンビネータの関係 古典命題論理や直観主義命題論理で,演繹定理を成立させる本質的な公理は 次の2つの公理でした.これら二つの公理は,カーリー・ハワードの同型定理と呼ばれる 定理やコンビネータ論理の S, K コンビネータと関係があります.
名称 公理スキーム THEN-1 A → (B→A) THEN-2 (A → (B→C)) → ((A→B) → (A→C)) コンビネータについては私のサイトの別ページ
コンビネータ論理(Combinatory Logic) のお話や
λ式から SKI を使った式への変換のトレースSKIコンビネータ AGAINにある程度詳しく書いていますので,興味のある方はそちらを参照して ください.S, K コンビネータは,簡単に書くと次のような機能を持つ 関数のようなものだと 思っていただけば良いと思います.S x y z =((S x) y) z = (x z) (y z)
K x y =(K x) y = x
括弧を省略すると前から括弧で括られていると解釈します.
u v w x = ((u v) w) x細かなことは省きますが,例えば,
(S K K) x → (K x) (K x) → xのように S と K だけで,色々な計算を表現することができます.これは恒等写像を表す
それで,これと命題論理の関係ですが,これらの文字の並びが命題論理の 含意(→)に関する公理
名称 公理スキーム THEN-1 A → (B→A) THEN-2 (A → (B→C)) → ((A→B) → (A→C)) に似ているねということです.K が THEN-1,S が THEN-2 に似ています.
(後はそのうち)
参考文献
Wikipedia の次の項目が参考になります
Propositional calculus (英)
結構な分量の記述があります.
Deduction theorem (英)
演繹定理の説明です.証明とか,それを使った証明の変換とか 詳しく書かれています.
Interpretation (logic) (英)
ここの「命題論理の意味論的な特徴づけ(2)- 一般的な枠組みでの定義 -」の項目は,Wikipedia のこの項目が役に立ちます.
Vilnis Detlovs, and Karlis Podnieks: Introduction to MathematicalLogic, May 24, 2017
数理論理学の教科書です.命題論理も書かれています. 検索すれば PDF が見つかると思います. "Hyper-textbook for students" とは書いてあるのですが,Creative Common のライセンスになっているので,見てよいのじゃないでしょうか( 学生用に書いたんだけど,一応,Creative Common だよとかで :-)).
ブール代数 (Boolean Algebras)
この項目の内容
はじめに
計算機をやっている人は,
{0, 1} の二値のブール代数 については勉強したことが あると思います.ここでは,それより一般化されたブール代数 を学習します.必要な知識として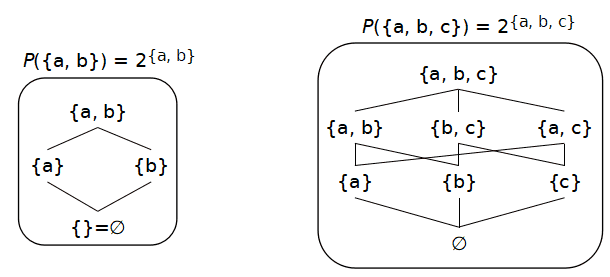
典型的なブール代数の例
(部分)順序集合(posets) と束論(lattice)の基礎 を仮定します.これらについては私のサイトの別ページ順序集合や束などに関する基本的な概念の説明で結構詳しく解説しています.そこの目次の「順序集合一般の基礎」 と「束論の基礎」 の 知識があれば十分です.それら全部を使う訳ではありません から, 自信がなくとも,とりあえず,ここを読んでいて,分からないことがあったら, 上記を参照してみると言うことでも良いと思います.
準備 束論で使う概念のちょっとした思い出しをしておきます.順序集合に関する知識に関して 自信がない場合や,束論の基礎的な知識をもう少し詳しく知っておきたい場合は,上で 言いましたように
順序集合や束などに関する基本的な概念の説明を参照してください.以下で必要になる概念をざっと列挙しておきます.
準備
- 順序集合 (S, ≤) が,
上半束(join semilattice) であるというのは,S の任意の二元 x, y∈S に上限 x∨y があることである.
- 順序集合 (S, ≤) が,
下半束(meet semilattice) であるというのは,S の任意の二元 x, y∈S に下限 x∧y があることである.
- 順序集合 (L, ≤) が上半束であり,かつ,下半束であるとき,
束(lattice) であるという.つまり,任意の二元 x, y に 対して,上限 x∨y が存在し,下限 x∧y が存在する順序集合である. ∨ や ∧ は L×L→L の演算子(二項関数)とも解釈することができ, また,上限,下限を求める演算子が定義されている代数系は順序集合としても束になるため, 束をある種の公理を満たす(L, ∨, ∧) という代数系と 見ることも多い.
- 束 (L, ∨, ∧) が次の2つの式を満たす時,
分配束(distributive lattice) であるという.L が束の場合は,これらの式は一方から他方が導かれるので,1つでも構わないが 両方の成立すると言うことを心に留めておくために両方書いておく.x ∧ (y ∨ z) = (x ∧ y) ∨ (x ∧ z) for ∀x, y, z∈L
x ∨ (y ∧ z) = (x ∨ y) ∧ (x ∨ z) for ∀x, y, z∈L
一般に,束であれば,次の図のように
は必ず成り立つので,分配束であるというのは,これが常に = になるという ことが特徴である.x ∧ (y ∨ z) ≥ (x ∧ y) ∨ (x ∧ z)
- 束 (L, ∨, ∧) に最小元,最大元がある場合は,それらを 0 と 1 で 表すことが多い.最小元,最大元があることを明記するために
(L, ∨, ∧, 0, 1) と書くこともある.
- 順序集合,束の
準同型 ,同型 は通常通りに定める. 詳しくは, 順序集合や束などに関する基本的な概念の説明 を参照.ブール代数を定義するためには,あと,
「否定」相当 がある束を定義した方が良いのですが, 準備が長くなるのと,それはしっかりやった方が良いので,本論に回します.
定義 ブール代数とは,一言で言ってしまえば,
可補的な分配束 のことです. とりあえず,さっさと定義だけは済ませておいて,その後で解説をしましょう.定義
補元(complement)と可補的な束(complemented lattice)
最小元 0 と最大元 1 がある束 (L, ∨, ∧, 0, 1) において,x∈L に 対し,y が,x ∧ y = 0を満たす時,y は x のx ∨ y = 1
補元(complement) であると言う.束 (L, ∨, ∧, 0, 1) で,任意の x∈L に補元があるとき, L を
可補的な束(complemented lattice) という.
ブール代数(boolean algebra)
(B, ∨, ∧, 0, 1) が分配束で可補的な束であるとき,これをブール代数(boolean algebra) であるという. 後で証明するが,分配束では補元はあったら一意に決まるので, ブール代数では,任意の x∈B に対して,補元を割り当てる 一項演算子があると思って良い.この演算子は¬ で表され, x の補元は¬x と表されることが多い. また,この補元を割り当てる演算子があることを明記するために,ブール代数を(B, ∨, ∧, ¬, 0, 1)と6項組で記すことも多い.ここでもこれらの記法を使う.
まず,上の定義の中で言った,
分配束の中では補元は一意に決まる ことを証明して 置きます. それには,次の図のように,y と y' を x の補元としたとき,
y = y ∧ 1 = y ∧ (x ∨ y')と
y' = y' ∧ 1 = y' ∧ (x ∨ y)をそれぞれ変形していって,両方とも
y ∧ y' = y' ∧ y になることを 確かめればできます.
とにかく,ここでは
ブール代数 とは,
分配束であり ,最小元 0 と最大元 1 があり ,任意の元 x に補元 ¬x が必ずある というような束であるということだけ頭に入れてください.
次に,一応,型どおりですがブール代数における準同型写像と同型写像を定義しておきます.
定義(準同型写像と同型写像) (B1, ∨1, ∧1, ¬1, 01, 11) と (B2, ∨2, ∧2, ¬2, 02, 12) を二つのブール代数とするとき, 写像 f : B1 → B2 が
準同型写像 であるとは, 次の式が成り立つことである.尚,B1 と B2 がブール代数である場合,上の 1, 2, 4, 5 が 成り立てば 3 は自動的に成り立つので,準同型であることを確かめるのに 必ずしも全部の式を調べる必要はない.
- f(x ∨1 y) = f(x) ∨2 f(y)
- f(x ∧1 y) = f(x) ∧2 f(y)
- f(¬1 x) = ¬2 f(x)
- f(01) = 02
- f(11) = 12
また,同時に準同型 g : B2 → B1 があり, g・f : B1 → B1 が B1 上での 恒等写像,f・g : B2 → B2 が B2 での 恒等写像であるとき,これら二つのブール代数は
同型 であると言い, f, g は同型写像であると言う.定義の中にも書きましたが,ブール代数でのすべての演算子の等式は一部の等式から 他の等式が導かれる場合がありますから,全部を調べないといけないということは ありません.例えば,等式 3 は f(¬x) が f(x) の補元になることを言っている 訳ですから,
f(x)∨2f(¬x) = 12を言えば良い訳ですが,これらは
f(x)∧2f(¬x) = 02f(x)∨2f(¬x) = f(x∨1(¬1x))= f(11)=12から言えます.
f(x)∧2f(¬x) = f(x∧1(¬1x))= f(01)=02
ブール代数の例 ここでいくつかブール代数の例をみておきます.
2 = {0, 1}
最小元と最大元が異なるブール代数で最も小さいものは2個の元だけからなる ブール代数です.これが通常,計算機に関する授業で教えられているブール代数ですね.
各演算子は次のように定義されます.
集合 S に対してその冪集合 (P(S), ∪, ∩, ¬, ∅, S)
集合 S に対して,その冪集合 P(S) = 2S はブール代数をなします.
各演算子は次のように定義されます.
X ∨ Y := X ∪ YX ∧ Y := X ∩ Y
¬ X := S - X
後でもう一度触れますが,有限のブール代数は,適当な集合 S に対して, この形のブール代数と同型になります.従って,要素の個数は必ず 2 のべき乗に なります.
集合 S の有限および余有限部分集合の集合
集合 S の部分集合 X⊆S が,|S - X| < ∞ のとき, X を余有限集合(cofinite set) ということにします. S の有限あるいは余有限集合の全体は,冪集合と同様に次の演算子でブール代数をなします.X ∨ Y := X ∪ YX ∧ Y := X ∩ Y
¬ X := S - X
¬X = S - X は,X が有限のとき余有限,X が余有限のとき 有限になることに注意してください.
S が無限集合のとき,このブール代数は S と同じ基数になります.したがって,冪集合 P(S) より遥かに小さな ブール代数になります.
集合 S の冪集合の部分集合で,S と ∅ を含み,∪, ∩, S-・ で閉じている集合族
B⊆P(S) が次の性質を持つときは,(B, ∪. ∩, S-・, ∅ S) はブール代数になります.ただし,ここで,S-・は,X に S-X を対応させる演算とします.
- ∅, S∈B
- X, Y∈B ならば X∪Y∈B
- X, Y∈B ならば X∩Y∈B
- X∈B ならば S-X∈B
B がこれらの演算で閉じていれば,Bの要素は集合ですから,もともと分配法則
X∩(Y ∪ Z) = (X∩Y) ∪ (X∩Z)は成り立つわけです.最小元 ∅ も最大元 S も B に入っていますし, 任意の X∈B に対して,補元 S - X も B に入っていますから, ブール代数の性質をすべて満たします.従って,例えば,次のような束はブール代数をなすことが分かります.
- 位相空間 (U, O) が与えられたとき,O の中の 開集合かつ閉集合である集合(clopen sets)の集合は通常の集合演算で ブール代数をなします
- 上に述べた有限および余有限な集合の集合もこの原理により ブール代数になることが分かります
区間代数(Interval algebras)
(L, ≤) を最小元を持つ全順序集合とするとき,と定義すると,Int(L) は,順序 ⊆ でブール代数になります.そのときの ∨, ∧, ¬ は,それぞれ集合の演算の ∪, ∩, ¬ です. このブール代数をInt(L) := L の冪集合 P(L) の部分集合で,半開区間 [a, b) のすべてを 含む最小の束ここで,a, b∈L に対して,[a, b) := {x∈L | a≤x<b}
また,b は ∞ でも良いとし,その場合,
[a, ∞) := {x∈L | a≤x}
とする.
区間代数(Interval algebra) と言います.区間代数は,Lindenbaum-Tarski 代数(下で説明)を研究するのに有用だそうです. また,可算集合(自然数と同じ基数の無限集合)のブール代数は何らかの区間代数に同型になるらしいです.この意義を明確に書くと,これは
ことを意味します.任意の可算集合のブール代数は,対応する最小元付の全順序集合 L により その構造が完全に決まる ちょっと,区間代数がどんなブール代数になるか例を使って見てみましょう.
L := N = {0, 1, 2, ...} としてみます.Int(N) には,すべての 有限集合が入っています.なぜなら,区間 [n, n+1) を考えれば,これは n だけからなる 集合で,区間代数には任意の有限個の区間の ∪ をとることができるからです. また,余有限な集合,つまり,その補集合が有限な集合も入っています.なぜなら,補集合は有限ですからその最大値 m があります.その余有限な集合は,m+1 以上の数を含む 必要がありますから,区間 [m+1, ∞) を含んでいます.あとの残りの有限個の数は それぞれ,区間 [n, n+1) で入れていけば良いので,余有限の元も含んでいるわけです. それ以外の形の集合は含むことができませんから,Int(N) は自然数の部分集合で 有限あるいは余有限の集合からなるブール代数ということになります.
リンデンバウム代数(Lindenbaum algebra or Lindenbaum–Tarski algebra)
命題記号 {p, q, r, ...} から ∨ や ∧ ¬ などの論理記号で組合せて作られる 命題の集合を L として,L に次の同値関係 ~を導入します.A~B iff A から B が証明でき,かつ,B から A が証明できるこのとき,L の同値関係 ~ による商空間 L/~ をリンデンバウム代数と呼ぶ. p∈L の同値類を [p] で表すとしたとき,[p] ∨ [q] := [p ∨ q]とすれば,L/~ はブール代数となります.[p] ∧ [q] := [p ∧ q]
¬ [p] := [¬ p]
ブール代数にならない有界分配束の例 3 := {0, 1/2, 1}
例えば,3 := {0, 1/2, 1} とし,x∨y = max(x, y), x∧y = min(x, y) とすると,3 は分配束になりますが,1/2 の補元はありません.なぜなら, a を 1/2 の補元とすると1/2 ∨ a = 1 ⇒ max(1/2, q) = 1 ⇒ a = 1となり,補元の性質を満たす a は存在しないからです.実際,次の図のように 何を持ってきても,1/2 の補元にはなりません.1/2 ∧ a = 0 ⇒ min(1/2, a) = 0 ⇒ a = 0
この例はあとの項目の ハイティング代数でも出てきて, ハイティング代数の例にはなっています. ハイティング代数は直観主義論理と呼ばれる論理のモデルになります.
性質
ブール代数における恒真性の確認方法
「任意のブール代数について,いくつかの変数を含む等式が恒真である必要十分条件は,それが二値のブール代数 2={0, 1} で恒真であることである.」とのことです.
有限ブール代数の型
有限ブール代数は,なんらかの集合 X の冪集合のブール代数と同型です. 従って,基数は常に 2 のべき乗です.
超フィルター(ultrafilter)との関係
B をブール代数とし,f : B→2 を全射である準同型とするとき, f-1(1) は超フィルターになる.逆に F⊂B が B の超フィルターなら,f を
f : B → 2とすれば,f はブール代数の準同型となり,F=f-1(1) である.f(b) = if (b∈F) then 1 else 0
(そのうち)
応用
(そのうち)
公理系による特徴づけ ブール代数は順序集合としてではなく,∨, ∧, ¬ という演算を持った 代数系として定義することもできます.ものによってはそのように定義してあるものも あると思います.そういうものを見たとき,十分馴染めるように,そのような定義に 含まれる公理の意味について見ておきましょう.
ブール代数を定義する公理系には色々あると思いますが,一つ,分かりやすい例を あげておきます.次の公理系の公理は多少重複があり,減らすことも可能ですが, 意味が分かりやすいので,まずは,これで理解して,他はここに帰着できるかどうかを 考えると良いと思います.
定義 (B, ∨, ∧, ¬ 0, 1) がブール代数であるとは,次の公理が満たされることで あるとする.ただし,∨ と ∧ は B の上の二項演算,¬ は B の上の単項演算, 0 と 1 は B の要素とする.
- 反射律
x ∨ x = x
x ∧ x = x
- 交換律
x ∨ y = y ∨ x
x ∧ y = y ∧ x
- 結合律
x ∨ (y ∨ z) = (x ∨ y) ∨ z
x ∧ (y ∧ z) = (x ∧ y) ∧ z
- 吸収律
x ∨ (x ∧ y) = x
x ∧ (x ∨ y) = x
- 分配律
x ∨ (y ∧ z) = (x ∧ y) ∨ (x ∧ z)
x ∧ (y ∨ z) = (x ∨ y) ∧ (x ∨ z)
- 単位性
x ∧ 1 = x
x ∨ 0 = 0
- 可補性
x ∨ (¬x) = 1
x ∧ (¬x) = 0
このような感じで沢山の等式が羅列されると意味を取りにくいと思います.でも,これらは,次の図の右側に書いたように解釈できて,本項目の最初に順序集合として定義したブール代数に丁度対応したものになっています.
最初の4種類の公理群で,B が束になっていることを読み取るのがコツですね. 残りのものはほぼ,公理の通りの意味ですから.
公理群は色々最適化することはできるでしょうが,
を頭に入れておけば,このような公理群は自分でも作ることが 出来る訳です.まあ,これもブール代数への一つの馴染み方なのかなと思います.ブール代数 = 可補的な分配束
参考文献
Wikipedia
これを書いている時点(2021.03.15)では 英語版 のBoolean algebra は とても詳しく,良い参考文献だと思います.Boolean algebra には2つの 項目
がありますが,Boolean algebra (structure) の方が,このページの 趣旨にあっているもので,もう一方は二値のブール代数についてだけ 記述してあるようです.
- Wikipedia: Boolean algebra (structure)
- Wikipedia: Boolean algebra
Stanford Rncyclopedia of Philosophy:
The Mathematics of Boolean Algebra
2021年3月16日時点では記述は短いですが,かなり密です. 区間代数とブール代数他,色々な理論との対応も載っています. Boolean-valued models (Cohen のフォーシングによる連続体仮説独立性への現代的なアプローチに関連)に 関する言及もあり,目を通しておくと参考になると思います.
現代のブール代数, S. コッペルベルク (著), 広瀬 健 (翻訳), 渕野 昌 (翻訳) , 1986
日本で「ブール代数」という名前がタイトルについている本を開くと {0, 1} の演算で,あと計算機の論理回路への応用が書いてある本で, ここで書いたような趣旨では使えないことが多いのですが,この本は そういった本ではなく,ここの趣旨にあった内容の詳しい本です.
イデアルとフィルター (Ideals and Filters)
この項目の内容
はじめに
ここでは主に束論におけるイデアルとフィルターの基本的なことを述べます. 順序集合においては,イデアルとフィルターは双対の概念で,順序を逆にすることで お互いに移りあう概念です.前半の定義では,イデアルとフィルターの両方を述べますが, このページの趣旨から,後半部分はフィルターを中心に記述します.
イデアル は基本的には代数学での環論などで登場するイデアルと同等の概念です. 要は, 何らかの準同型 h : R1 → R2 における, 0∈R2 の逆像 h-1(0) です. 荒っぽくいうと R1 の中で 0 を演じる集団です.フィルター は環論などの なかに直接対応する概念はありません.束論においては, フィルターはイデアルの双対の概念ですが,初心者にとって, 理解しにくい概念だと思います.それは思いもしないような 使われ方をすることがあるからです.定義をみれば,イデアル は束の下方にある,ちょっと上に張っているような形状をした集合 で,逆にフィルター は束の上方にあり,ちょっと下に張った集合 です.
しかし, 時々,フィルターは
真偽値の真 であるような使われ方をすることがあります. これは特に次の項目で述べる「超フィルター(ultrafilter)」 の時にそのような使われ方を することがあります.この項目では,まず,イデアルとフィルターに関して基本的な事柄をまとめて, 次の超フィルターの学習の準備とします.
定義
束におけるイデアルとフィルター
束におけるイデアルとフィルターを定義しておきます.
定義 (L, ≤) を束とする.このとき,
- I⊆L が
イデアル(ideal) であるとは,I が次の条件を満たすことであるとする.
- (空集合でない) I は ∅ ではない
- (下に閉じている) x∈I かつ y∈L かつ y≤x ならば y∈I
- (∨ で閉じている) x, y∈I ならば,x∨y∈I
- イデアル I⊆L は,L と真の部分集合であるとき(つまり,L とは 等しくないとき),
proper であると言う.
- イデアル I が,p∈L を含む最小のフィルターであるとき,I を
principal ideal であるといい,p をprincipal element であると言う.これは
↓p := {x∈L | x≤p}と同じである.
- proper イデアル I が次の条件を満たす時,I を
prime で あるという.x∧y∈I ならば x∈I または y∈I
- イデアル I を真に含むイデアルが L 以外に無いとき,I を
極大(maximal) であるという(通常の,包含関係に関する極大の概念であるが,重要なので 項目を起こしておく).
フィルターはイデアルの
双対 の概念(向きを逆にした概念)であるので,ほぼ上の定義の双対を繰り返す ことになるが,このページの話の流れではフィルターの方が主になるので, しっかり概念に馴染んで欲しい..
- F⊆L が
フィルター(filter) であるとは F が次の条件を満たすことであるとする.
- (空集合でない) F は ∅ ではない
- (上に閉じている) x∈F かつ y∈L かつ x≤y ならば y∈F
- (∧ で閉じている) x, y∈F ならば,x∧y∈F
- フィルター F⊆L は,L と真の部分集合であるとき(つまり,L とは 等しくないとき),
proper であると言う.
- フィルター F が,p∈L を含む最小のフィルターであるとき,F を
principal filter であるといい,p をprincipal element であると言う.これは
↑p := {x∈L | x≥p}と同じである.
- proper フィルター F が次の条件を満たす時,F を
prime で あるという.x∨y∈F ならば x∈F または y∈F
- フィルター F を真に含むフィルターが L 以外に無いとき,F を
極大(maximal) であるという(通常の,包含関係に関する極大の概念であるが,重要なので 項目を起こしておく).極大なフィルターはしばしば,超フィルター (ultrafilter) と呼ばれる.ただし,L がブール代数のときだけ, 超フィルターという呼び方を使うこともあるとのこと.
2021.03.17
集合の上のフィルター
ブール代数のところでも書きましたが,S を集合とすると,冪集合 P(S) は ブール代数=可補的な分配束になります.この束におけるフィルターを簡単に
集合 S の上のフィルター ということがあります. 束の言葉でなく,集合の言葉で書くと次のような定義になります.定義 集合の上のフィルター S を集合とするとき,F⊆P(S) が
フィルター であるというのは,F が次の性質を満たす時にいう.
- F は空集合ではない
- X∈F かつ X⊆Y なら F∈F
- X, Y∈F ならば,X∩Y∈F
F は,F を真に含むフィルターが P(S) 以外に無いとき,
極大フィルター(maximal filter) あるいは,超フィルター(ultrafilter) であるという.
(残りはそのうち)
超フィルター (Ultrafilters)
上でイデアルとフィルターの基礎を学びました.ここではフィルターに特化して, その極大なフィルター,超フィルター(ultrafilter)について見ていきます. 超フィルターは超準解析で実数を拡大して無限小のような数を作り出すときに 使われることもあます.その場合,超フィルターは,特殊な真偽値のような 使われ方をして,面食らうことがあります.ここではそういう側面を見ていこうと 思います.
この項目の内容
はじめに
(そのうち)
定義
超フィルター(ultrafilter)の定義は,上の イデアルとフィルター (Ideals and Filters) で行いましたが,フィルターの部分だけ繰り返しておきます.定義
- F⊆L が
フィルター(filter) であるとは F が次の条件を満たすことであるとする.
- (空集合でない) F は ∅ ではない
- (上に閉じている) x∈F かつ y∈L かつ x≤y ならば y∈F
- (∧ で閉じている) x, y∈F ならば,x∧y∈F
- フィルター F⊆L は,L と真の部分集合であるとき(つまり,L とは 等しくないとき),
proper であると言う.
- フィルター F が,p∈L を含む最小のフィルターであるとき,F を
principal filter であるといい,p をprincipal element であると言う.これは
↑p := {x∈L | x≥p}と同じである.
- proper フィルター F が次の条件を満たす時,F を
prime で あるという.x∨y∈F ならば x∈F または y∈F
- フィルター F を真に含むフィルターが L 以外に無いとき,F を
極大(maximal) であるという(通常の,包含関係に関する極大の概念であるが,重要なので 項目を起こしておく).極大なフィルターはしばしば,超フィルター (ultrafilter) と呼ばれる.ただし,L がブール代数のときだけ, 超フィルターという呼び方を使うこともあるとのこと.
2021.03.17(残りはそのうち)
ハイティング代数 (Heyting Algebras)
ここでは直観主義論理のモデルにも使われるハイティング代数に ついて解説します.以前述べたブール代数はハイティング代数になりますが, 逆は必ずしもなりたちません.
この項目の内容
はじめに
(そのうち)
定義
まずは,ハイティング代数の定義を書いておきましょう.
定義(ハイティング代数) 有界束(最小元と最大元がある束)(H, ∨, ∧ 0, 1) が
ハイティング代数(Heyting algebra) であるとは H が次の条件を満たす時にいう.任意の a, b∈H に対して,ある c∈H があって,(a ∧ x)≤ b ⇔ x≤c
が成り立つ.
このような c が存在すればそれは a と b に対して一意に決まるので,この c を
a→b と表し,a と b のimplication と呼ぶ.上の定義でも図を入れましたが,少しゴチャっとしていて,a, b, c, x の関係が 掴みにくいかもしれません.これは H を二つ書くことにより多少改善します. a ∧ x を,x から a ∧ x へ変換する関数 (a ∧ ・) と思うのです. このような見方を次の図に示します.
x から x ∧ a を割り当てる関数があるとします.x にその関数を適用して 得られた結果 a ∧ x が b∈H 以下であるための必要十分条件が, c∈H を適切にとって,x≤c と出来る束であるというのが,ハイティング代数の 定義になります.束論の基礎のページ 順序集合や束などに関する基本的な概念の説明 で
ガロア接続 を勉強してきたなどで,ガロア接続をご存じの方は,と理解すれば良いです.ハイティング代数 とは,f : H → H, f(x) := a ∧ x に対して, ガロア接続をなす逆向きの写像 g : H → H が存在する束のこと. g(b) をa→b と書く.a→b の直感的な意味は,
「a ならば b」 です.したがって,数理論理学の表現 で言えば,ということです.このページで述べたブール代数は a→b を ¬a ∨ b と すれば,ハイティング代数になります.しかし,ハイティング代数が常にブール代数に なるとは限りません.一般には,ハイティング代数はブール代数より少しハイティング代数 H とは,(真偽値の集合の)代数である
- false (0), true (1) を含む真偽値からなり,
- ∨, ∧ という論理結合子で真偽値を結合して行くことができ,
- 任意の a, b∈H に対して,
「a ならば b」(a→b) という 真偽値が存在する「弱い」 のです.ハイティング 代数は,排中律 a ∨ (¬a)が必ずしも成り立つとは限らない直観主義論理 のモデルに使われます.
2021.03.17
ハイティング代数の例
いくつかハイティング代数の例を見ていきましょう.
ブール代数
ブール代数はすべてハイティング代数です.
有界の全順序集合 (L, ≤, 0, 1)
この場合,上限 ∨ と 下限 ∧ は次の式で表されます.x ∨ y = max(x, y)
x ∧ y = min(x, y)このとき,a ∧x = min(a, x)≤b が,x≤c という形に 書き直されるか考えてみると,次の図のように c を
1 if a≤bとすればよい.
b otherwise
3値ハイティング代数 {0, 1/2, 1}
上記のように,3 := {0, 1/2, 1} を,数の大きさを使って全順序集合と考えると,x ∨ y = max(x, y)です.また,¬x そのものは無いので疑似否定として ¬ x := x→0 とすると
x ∧ y = min(x, y)
x → y = if(x ≤ y, 1, y)1/2 ∨ (¬ 1/2) = 1/2 ∨ (1/2 → 0) = 1/2 ∨ 0 = 1/2となり,この場合,排中律 x ∨ ¬ x = 1 は成立しません .この例は後ろのハイティング代数の応用(直観主義命題論理の解釈)で,直観主義論理の解釈について定義した後で,直観主義論理では必ずしも 排中律が成立しないと言うことを示す時使います.
ハイティング代数の性質
ハイティング代数は分配束 x ∧ (y ∨ z) = (x ∧ y) ∨ (x ∧ z)
x ∨ (y ∧ z) = (x ∨ y) ∧ (x ∨ z)
二重否定は元の元以上になる ¬x := x → 0 とすると
x ≤ ¬¬x
[Proof]¬x=x→0 だから,(¬x)∧x ≤ 0. ∧ は可換だから x∧¬x ≤ 0
¬¬x = ¬x→0 だから,¬¬x は,y∧¬x ≤ 0 を成立させる最大の y である.上の式から,y=x とすればこれを満たす.
y はこのような元の最大元であるから,x≤y.すなわち,x≤¬¬x.
[Q.E.D.]
(そのうち)
ハイティング代数とブール代数の関係 ブール代数は
- 分配束であり,
- 最小元 0 と最大元 1 があり,
- 任意の元 x に補元 ¬x が必ずある
という束でした.ブール代数は,補元を使って ・→・ を
x →y := ¬x ∨ yと定義すればハイティング代数に なります.一方,ハイティング代数は有界(最大元と最小元はある)であり, また,上で書いたように分配束でもありますから,補元があればブール代数に なります.次の定理はハイティング代数がブール代数になる条件を示しています.
定理 H をハイティング代数とする.x∈H に対して,¬x := x→0 とするとき, H がブール代数になる必要十分条件は
¬¬x≤xを満たすことである.
ハイティング代数の応用(直観主義命題論理の解釈)
2021.07.15ハイティング代数は,このページの最初の方で紹介した 直観主義命題論理を解釈することができます. ここでは直観主義命題論理の公理群で排中律(PEM : Principle of Excluded Middle)が 必ずしも成立しないことを示す簡単な方法を提供します.また, 「直観主義命題論理の解釈」という用語もきちんと定義して説明しておきます.
まず,直観主義命題論理の言語(記号)と公理群,推論規則は先の 直観主義命題論理を見て, よく思い出しておいてください.まあ,古典論理から
を抜いただけですけど.NOT-3 A ∨ ¬A (排中律,PEM : Principle of Excluded Middle)ここでは,この公理群に無い排中律が他の公理からは 導かれないということを「直観主義命題論理の解釈」を定義してから示します.
直観主義命題論理の解釈 H をハイティング代数とします.命題変数の集合を V とします.V から H への 関数
ρ : V → Hを変数の割り当て ということにします.命題の集合を P とするとき, ρ は次のように帰納的にρ' : P → Hに拡張することができます(V ⊆ P に注意).
- ρ'(A) := ρ(A) for A∈V
- ρ'(A ∨ B) := ρ'(A) ∨ ρ'(B)
- ρ'(A ∧ B) := ρ'(A) ∧ ρ'(B)
- ρ'(A → B) := ρ'(A) → ρ'(B)
- ρ'(¬A) := ρ'(A) → 0 (0∈H)
このように定義された ρ' P → H を直観主義命題論理の
解釈 と呼ぶことにします.また,記号の乱用になりますが,ρ' も ρ と書くことにします.ρ を直観主義命題論理の解釈とするとき,次の2つのことが成立します.
直観主義命題論理の公理スキーム群は ρ ですべて 1∈H に移される. 直観主義命題論理の公理には,THEN-1~2,AND-1~3,OR-1~3,NOT-1~2 があります. THEN-1 A → (B → A) で確かめてみましょう.
x = ρ(A → (B → A)) は,ハイティング代数の → の定義からx ∧ ρ(A) ≤ ρ(B → A) となる最大の x (*)また,ρ(B → A) は y ∧ ρ(B) ≤ ρ(A) となる最大の y
ρ(A) ∧ ρ(B) ≤ ρ(A) だから y := ρ(B → A) ≥ ρ(A) は言える
ということは
x=1 (H の最大元)で上の (*) は成立する
ρ(A)=1 かつ ρ(A→B)=1 なら ρ(B)=1. これは x = ρ(A→B) が,x ∧ ρ(B) ≤ ρ(B) を満たす 最大の元という定義であり,それが 1 ということから,1 &and 1 ≤ ρ(B) と なり,ρ(B) = 1 となります.
つまり,モーダスポーネンスは命題の解釈が1であることを保つということです.
さて,いよいよ,排中律 A ∨ ¬A が無条件に成り立たないことの証明です. これは, ハイティング代数 3 := {0, 1/2, 1} とρ(A)=1/2 の割り当てを 使って解釈 ρ を作成すると,
ρ(A ∨ ¬A) = ρ(A) ∨ (ρ(A) → 0)となり,ρ(A ∨ ¬A) が 1 にはならない例が見つかることから示すことができます.
= 1/2 ∨ (1/2 → 0) = 1/2 ∨ 1/2 = 1/2
ハイティング代数の中のブール代数 次のような double negation の写像を考えることにより, ハイティング代数 H の中にブール代数の部分を見つけることができます.
¬¬ : H → Hx → 0 は,→ で否定 ¬ x を定義するときの式なので,この写像の意図は 二重に否定をとることです.¬¬(x) := (x → 0) → 0
この ¬¬ による H の像 ¬¬(H) ⊆ H は実はブール代数になる. このページの最初の方,「命題論理」の中の「古典命題論理と直観主義命題論理の関係」で Gödel-Genzen double negation transformationについて述べました. すなわち,古典命題論理がこのdouble negation transformationで, 直観主義命題論理に埋め込むことができるという性質についてです. 直観主義命題論理がハイティング代数 H の解釈を持っていたとします.このとき, 上で述べた H の中のブール代数 ¬¬(H) は,この埋め込まれた 古典命題論理の解釈になります.証明はここでは割愛します.
参考文献
Wikipedia の Heyting algebra 英語版
かなり詳しく書かれており,非常に良い参考資料だと思います. このページを書くにあたって相当参考にさせてもらいました.
圏論を勉強しよう
束論を勉強しよう