概要説明

Tom Leinster : Basic Category Theory,

2014

レンスター (Leinster) の本の 2014 年版 arXiv 版の PDF は

Basic Category Theory (arXiv)

ところで，これを DIY で簡易製本したものが， これです． こちらは，それを開いたところです．マーカーで 印をつけたり，派手に書き込んだり，結構やりたい放題です．皆さんもこんな本で勉強したくなったでしょう．簡易製本の方法をこちらに 載せましたのでご興味があれば，そちらもよろしく．

例によって私の読み間違いがあるかもしれませんので，あくまでどんなことが 書いてあるのかおよその参考にするだけで，内容はご自分で読んでください．

本の全体像

こちらの本は少し薄くて

183 pages, 107 exercises

本の構成は，上の図のように，まず第１章で圏論の基本的な概念と用語を定義してしまいます． 次に圏論の３つの柱，Adjoints, Representables, Limits/Colimits を説明し， 最後にそれらの関係を述べるという構造です．ただし，２つ目の柱，Representables は 一般の圏を集合の圏を利用して表現しようという内容なので，その前にちょっとした幕間が あります．ここでは，集合の性質を圏を使って表現してみることや，圏の大きさに関する 注意，そして歴史的な事柄が書かれています．幕間の第１節（集合の性質を圏を使って表現して みる）の内容は彼の別の論文 Rethinking Set Theory (2012年) とよく似ています．それについては こちら で概要を書きました．

こちらの本は，Awodey の本と違って，各章の扉の説明がしっかり書いてあるので， 忠実にそれを読み解くだけでも全体の内容がかなり分かります．

このページの図は

The PDF of the fort explanations in this page

1. Categories, functors and natural transformations

   まずは圏論の基本的な概念と用語を学びます．たぶん，最初は "Natural transformation"と いう概念がつかみにくいと思いますが，重要な概念なので，多くの例にあたってみたり， 図を何度も描いてみたりして習熟してください．この章の扉の説明では，もともと圏論は Natural transformation を厳密に定義するために生まれたとのことです．

   
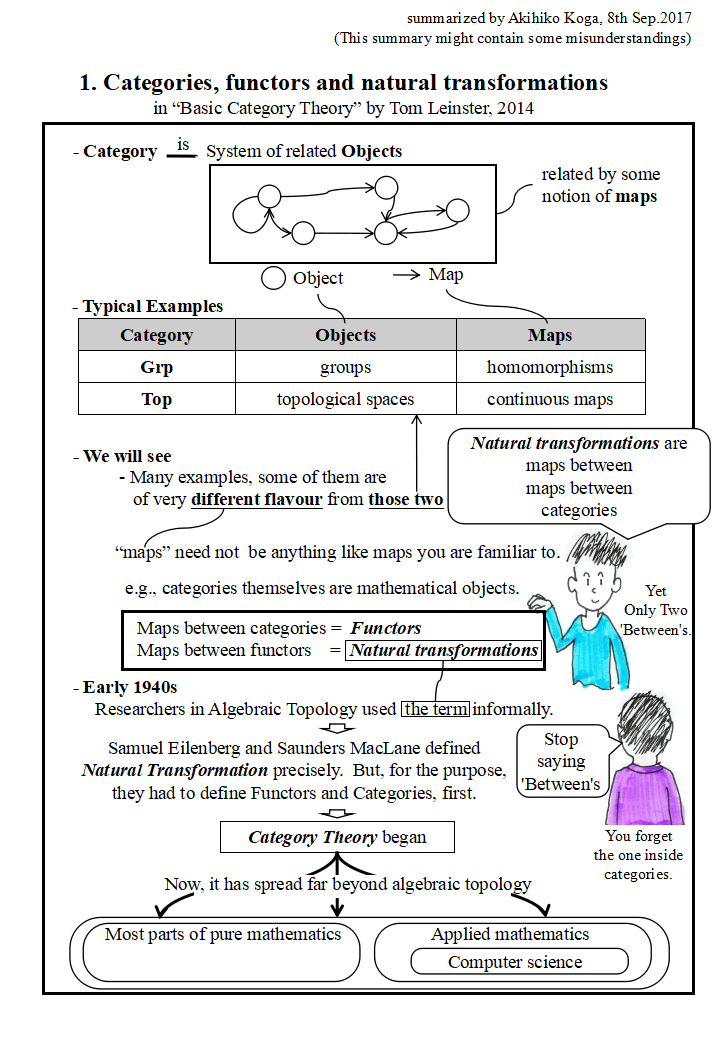
   一応，図の内容をざっと日本語で説明しておきます(2019.01.16 (水) 追加)．

   まず，圏とは「オブジェクト（なにか「もの」）」のシステムです．「システム」と いうからには，単なる集まりでなく何か構造があります．それは射（map）です． 「オブジェクト」は「射（maps）」で関係づけられています．そういうものが圏です． 圏とはオブジェクトの集まりと，そのオブジェクトの間に射があって，その射同士の 合成ができて，ある種の条件を満たす「システム」を言います．こういう「システム」として数学上の同じような性質を持っている「モノ」の「システム」を扱おうということです．

   典型的な圏には，群の圏 Grp，位相空間の圏 Topなどがあります． 群の圏 Grpでは「オブジェクト」は群であり，射は個々の群の間の準同型です． 位相空間の圏 Topでは「オブジェクト」は位相空間で，射は個々の位相空間の 間の連続写像です．

   私たちは非常に沢山の例を見て行くことになります．その中には上に挙げた二つとは， ずいぶん趣が違うものがあります．「射」はあなたが馴染みの深いなにものか（例えば 関数）である必要は ありません．例えば，圏の集まりさえも圏になります．このとき，圏から圏への射は 関手（functor）と呼ばれます．さらに，関手から関手の射も考えられます．これは 自然変換（natural transformation）と呼ばれます（ここは高階になっていきますので 最初は捉えにくいかもしれませんが，何度も証明を追ったり，例にあたることで慣れて行ってください）．

   1940 年代，代数的トポロジーの研究者達は，この「自然変換」という用語を非形式的に使っていました．アイレンバーグとマクレーンは，この「自然変換」を正確に定義しました． しかし，そのためには彼らはまず圏と関手を定義する必要がありました．

   このようにして圏論という理論が出来上がってきました．今日，圏論は，代数的トポロジーを はるかに超えて，殆どの数学の領域，そして計算機科学を含む応用数学に広がっていきました（とさ）．

2. Adjoints

   ここでは Adjoints を学びます．Adjoints は２つの圏からお互いに相手に向かって 関手（functor）が定義され，それらがある種の条件を満たすことにより，お互いに 拘束しあっているものです．これらの裏にはある種の同型が隠れています．ここでは 図の一番左の定義の後に沢山の例に触れ，次に最初の定義と同値な２つの定義を 述べます．これら３つの定義はそれぞれ，ある種の直観を我々に与えてくれます． Leinster によると，Adjoints を知ることは，あなたの数学の工具箱にとても 貴重な工具を加えることになると言うことです．

   
   

3. Interlude on sets

   集合論に関する幕間です．幕間ということは気楽に読んでよいということなんでしょうね．

   なんでここに集合論の幕間があるかというと，次の Representables で盛大に集合を使うからです． Representables では米田の埋め込み，米田のレンマが登場します．これらは，圏のオブジェクトを，集合を値としてとる関手で表現することに関係しています．

   
   

   ３つの話題があります．

   １つ目は集合の性質を圏論的に表現してみること．集合論は，要素を含む，含まないの関係から 構築することができますが，普段の数学では，その原理的なところまで降りて行かなくて， 直積がとれるとか，直和がとれるとか，集合から集合への関数の集合が作れるとか，もう少し 上のレイヤーでの性質を使います．一つ目のお話は，このレイヤーの性質を圏論的に表現するというお話です．このような取り組みを見ると，集合の圏論的な記述はオブジェクト指向言語のインタフェースにあたるのかもしれません．つまり，属する・属しないに基づく集合論はその実装で， 圏論的に抽出した特徴を持てば，もしかしたら，別の実装を持っても良いとか．

   二つ目は，「コレクション」の大きい・小さいです．たぶん，皆さんも，集合論で，「すべての集合の集合」を考えると矛盾が生じるというのはご存知と思います．「あまりにも大きなサイズの集合を考えると矛盾がでる」というように表現されることが多いと思います． ここではコレクションのサイズとして，small と large を導入します．圏論の中でも 普段はあまり気にしませんが，例えば米田のレンマについては，射のコレクションが集合に 収まる場合（smallである場合）など，意識が必要な場合があります．この本でも， 第６章の Adjoint Functor Theorem では本質的に必要になってくるという注意書きがあります．

   最後は集合論の簡単な歴史です．Cantor の集合論，集合の Type，Membership に基づく集合論（ZFC），今日的な集合論，いくつかのコメントがあります．この節の内容はこの本の後では使いませんが，知っておくと有益な perspective を得られると書いてあります．

   実は，この章の内容は，Leinster の別の論文

   Tom Leinster: Rethinking set theory, 2012, pp1-8

   とかなり重複しています．こちらは8ページで短く，分かりやすい論文です．こちらの論文を 先に読んでおくと，この章は読みやすいかもしれません．この主張は，Leinstert 独自のものではなく， William Lawvere という人が言ったことを分かりやすく書いたということみたいです（この William Lawvere も圏論ではいろいろな成果を出して，よい入門書も書かれた人みたいです）． Rethinking set theory については，私の別のページ

   集合論(Set Theory)

   の方にも短い解説を書きました．

   この Rethinking set theory については，やはり， 結構な議論（賛否）があるみたいです．次のURLは，Leinster の知り合い（圏で集合を特徴づけるのに反対の人）が立ち上げた ブログのようですが，Leinster ご本人も参加されて延々と議論がなされています．

   Asaf Karagila : On Leinster’s “Rethinking set theory

   私は，英語を読むのも疲れるので，最初のいくつかの議論しか読めていません．

   最後に，この章のまとめ図に関しては，あまり気の利いたイラスト＋ジョークを書けませんでした． 数学基礎論（Foundation）のお話は下手に意見表明してしまうと，気に障る人が多いかなと思うと， 何か思いついても躊躇してしまうのです． それで，アイザック・アシモフの「銀河帝国の興亡」ネタ（Foundationが出てくる）に逃れたのですが，古くてわかる人はあまりいないでしょうね．

4. Representables

   圏の表現に関する章です．圏は射によってお互いに相手を見ているオブジェクトの世界です． それぞれのオブジェクトにはそれぞれの見方（View）があります．この図にはいくつかの例を 表にして示してあります．例えば，位相空間の圏では，その中のオブジェクト R (実数の集合）は，ほかの位相空間の中に自分の像，つまり曲線を見ています（Leinster は，「見る」という言葉を使っていますが，相手を見るというより，相手の中に自分の像を見るといった方が正しい表現のように思います.むしろ，こちらの方が見られているという関係に見えます．）．

   今の例は，見る立場でしたが，双対をとって見られる立場というものも あります（上の考察からするとこちらの方が見るという感じに近いかもしれません）．これらの，「オブジェクトを見る，見られる」というテーマは，我々を， 圏の表現のテーマへと，自然に導きます．

   
   

5. Limits

   我々は，すでにUniversal Property に対する２つのアプローチ（Adjoints, Representables）を学びました．ここでは３つの目アプローチ，Limits/Colimits を学びます．数学では， ある概念を作り出す方法として，ある種のオブジェクトと射の集まりをとってきて，それらに 対するある関係にあるものを新しいものとして作り出すことがあります．このとき，Limits/Colimits を作り出していることが結構多いです． 例えば，群論で群Gから群Hへ準同型 h があるとき，その準同型の核 ker(h) という概念が ありますが（群論では G の中のある正規部分群），これは Limit にあたります．また，２つの整数の最小公倍数は，割り切れるという関係の順序を整数に導入した時の Colimit になっています．ここではこのような Limits/Colimits を学習します．

   
   

6. Adjoints, representables and limits

   最後の章は，これまで学んだ Adjoints (随伴関手），Representables, Limits/Colimits (極限/余極限) の関係です．

   
   

   これらは，Universal property を表現するためのアプローチで，基本的に三つの中の一つの方法で 表現できるものは他の二つの方法でも表現できます．それはあたかも，平面上の点が デカルト座標でも極座標でも表現でき，それぞれ注目している特徴寮が違うだけという状況と 似ています．

   この章は，このことを示して終わりなのかなと思ったら，そうではなくてすごく沢山の ことが書いてあります．ハイライトは，つぎの５つです（ちょっとこちらの順番が図の中で上から下へ並んでいませんが）．

   1. Presheave [A^op, Set] は極限，余極限を持つ．

   2. Representable A(-, A) は，極限を保つ

   3. Presheave [A^op, Set] の中の任意の関手 F は，Representables の 適当な図式の余極限として表すことができる．

   4. Left adjoint を持つ関手は極限を保つ．
      ある条件下で，

      Left adjoint を持つ <=> その関手が極限を保つ

      という形の，Adjoint Functor Theorems と呼ばれる一連の定理があります．

      (5つのハイライトの中でこの項目 4 だけが浮いているような気がします）

   5. Topos への道
      上記 2 と 3 および米田のレンマなどからPresheave [A^op, Set] は Exponentails を持つことが言える．上記 1 から Presheave [A^op, Set] は任意の有限 products を持つことが言えるので，Presheave [A^op, Set] は Cartesian Closed Category (CCC) と呼ばれるものであることが分かる． さらに，1 から，有限極限を持つことが言える．また，subobject classifier と呼ばれる真偽値を抽象化したものも持つことが証明されるので，Presheave [A^op, Set] は， Topos になる．これは，論理学と幾何学の主題を一緒にする信じられないお話の始まりへと 進んでいく．

7. Appendix Proof of the general adjoint functor theorem
   ここには章の説明はありません．

8. Further reading
   ここには章の説明はありません．

ホームページトップ(Top of My Homepage)