圏論の理論で モナド (Monads) というものがあります．例えば，Steve Awodey の Category Theory の最後の章は，モナドと代数の章です．一般的な圏論の教科書では，モナドが随伴関手の合成であること，モナドから随伴関手への分解方法もあることなどの説明はありますが，どのように使われるのかまでは説明されません．
圏論の理論で モナド (Monads) というものがあります．例えば，Steve Awodey の Category Theory の最後の章は，モナドと代数の章です．一般的な圏論の教科書では，モナドが随伴関手の合成であること，モナドから随伴関手への分解方法もあることなどの説明はありますが，どのように使われるのかまでは説明されません．
一方，モナドは関数型言語の中で副作用を閉じ込めるのに利用されているなどの 宣伝がなされることがあり，理論に興味があるプログラマたちの関心を集めています． これを言いだしたのは，Eugenio Moggi 氏でしょうか，wikipedia をみると，文献
Moggi, Eugenio (1991). "Notions of Computation and Monads" (PDF). Information and Computation. 93 (1): 55–92. doi:10.1016/0890-5401(91)90052-4.で，プログラムを構造化するためのモナドの一般的な使い方を示したとあります．
このほかにも，なにやら，モナドはいろいろ応用がありそうです．そこで，ここではモナドの利用を調査をしてみようと思います．読んだ，あるいは，読もうかなと思っている文献を次にあげていきます．読んだものは，Abstract に書いてある程度の概要もつけてあります（読んでなくとも Abstract だけ読んでとりあえずつけたものもありますが）．
文献への直接のリンクは張らないことの方が多いので，興味があれば，文献のタイトルや著者で
ぐぐって調べてください．
Haskell のモナドに関するものなど，Moggi の話題にごく近いもの．
Moggi の話題と直接の関連はないかもしれない計算機科学でのモナドの利用． プログラミング言語のセマンティックスなどもここに集めるつもりなので，上との切れ目がはっきりするかは分かりません．また，今のところ論理学（Logic）もここに入れる積りです．
代数，そのほか，ソフトウェアに限らないモナドの応用．これも上の２つと重複があるるかもしれません．応用を集めてある文献では計算機科学の応用も書いてある可能性があるので．
モナドの理論一般についての参考書，文献．圏論で，モナドのことをある程度取り上げているものも含みます．
本当はこの論文を読むべきなんでしょうね． とりあえず，アブストラクトと最初の数ページだけ読みましたので， アブストラクトの図を載せておきます．
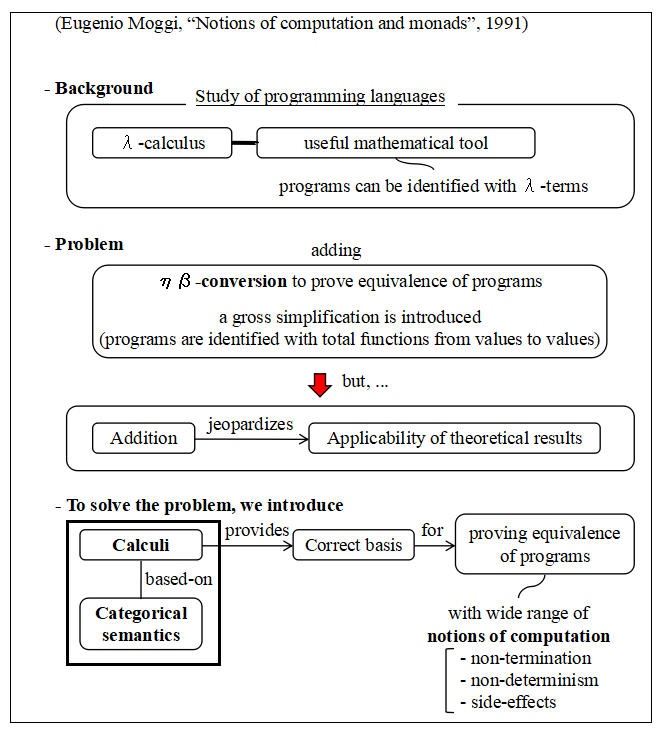
一応，図を読み上げておきます． λ-calculus は，プログラムをλ-term で表現することができ，プログラミング言語の研究の ための有用な数学的ツールである．しかし，プログラムの同値性の証明体系を強力にしようとして ηβ変換を導入すると，αβ変換だけのときと違う問題が生じ，λ-calculus の成果の適用を 危うくする．（α変換，β変換，η変換は，wikipedia の「ラムダ計算」に定義が載っています）． ここでは，この問題を解決するために，Categorical semantics に基づいた計算 (Calcui) を提案する．これは，広い範囲の計算の概念（例外処理，非決定性，副作用）を 持ったプログラムの同値性を証明する正しい基盤を提供する．
（あれ？ η変換の話だったと思ったのですが，種々の計算の概念（Notion of computation）を 持つプログラムの同値性証明基盤に変わってるような．この２つはイクオールなんでしょうか？ 不勉強で私はこの２つの関係を正しく把握していません．読んでみればわかるのかな？）
論文の中身は，最初の５ページくらいで種々の「計算」に対応するモナドの例を圏論的に 例示しています（Partiality, nondeterminism, side-effects, exceptions, continuations）． これらは圏論の知識がないと読めません（たぶん，Awodey の Category Theory 位以上． 薄いレクチャーノートでも良いので，モナドとか代数とかが出てくるもの）
第２章では，モナドを持った簡単なプログラミング言語を定義して，その証明の体系を 与えているようです．論文の残りは，
3. Extending the simple metalanguage
4. Strong monads over a topos
Conclusions and further research
となっています．圏論に詳しくて興味のある方は読んでみてください．
著者の Phillip Wadler は Haskell の設計に係わった人なんですね．
この論文もアブストラクトから起こした図を載せておきます．
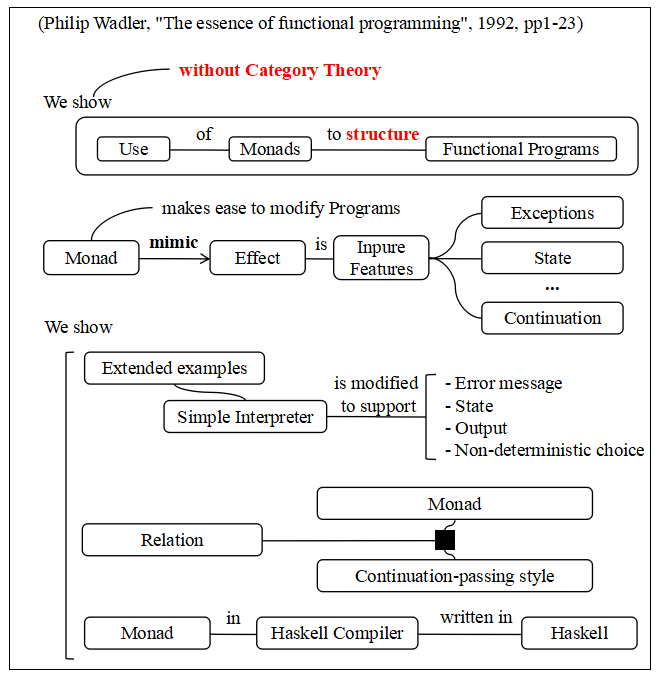
一応説明すると（図を読み上げるだけですが），この論文では関数型プログラムを構造化するためのモナドの使い方を，「圏論なしで」示します．「圏論なしで」というところが嬉しいですね． もっとも， このページは，「圏論を勉強しよう」のページの子ページなわけですから，こういうことを 言ってはいけないんですけど．
で，モナドは Effect を模倣（mimic）することでプログラムの変更を容易にします．ここで Effect とは日本語では「副作用」と 言われるもので，例外，状態，継続（Continuation）のような Inpure な機能のことです．継続は Scheme などにある，ちょっと変わった制御機能ですね．制御情報自身を他のデータと同様に扱うことによって大域脱出とか大域突入みたいなことができるという．
この論文では次の３つのことを示します．まず第１に簡単なインタープリタを改造していくことで，エラーメッセージ，状態，出力，非決定論的な選択の機能を追加していく例題を示します．次にモナドと継続パッシングスタイル（関数呼び出しのパラメータをうまく使うことで継続を渡していくコーディングスタイル）の関係を示します．最後に，Haskell 自身で書かれた Haskell Compiler の中のモナドを示します．
手元にある，この論文を印刷したものを見ると，線が１つも引かれていないので， 私は読んでないんだと思います．とりあえず，上のことはアブストラクトに書いてあることです． 読んだら感想を書くかもしれません．
アブストラクトを読むと次の図に示すような論文です．
Haskell のモナドは関数 a→ m b を関数 m a → m b にマッピングする機構を提供します．ここで，このマッピングは m （モナド）に依存し，モナドは， (1) 非決定論性から failure handling まで広い範囲の機能を可能にし，また， (2) プログラムを副作用（Effects）のあるものと無いものに，関数性を保ったまま分離することを可能にします．（モナドを実装した）プログラミング言語 Haskell はモナドプログラミングのための構文 "do Notation" を提供します．この論文では List, Maybe, IO Monads を含むモナドの例を紹介します．
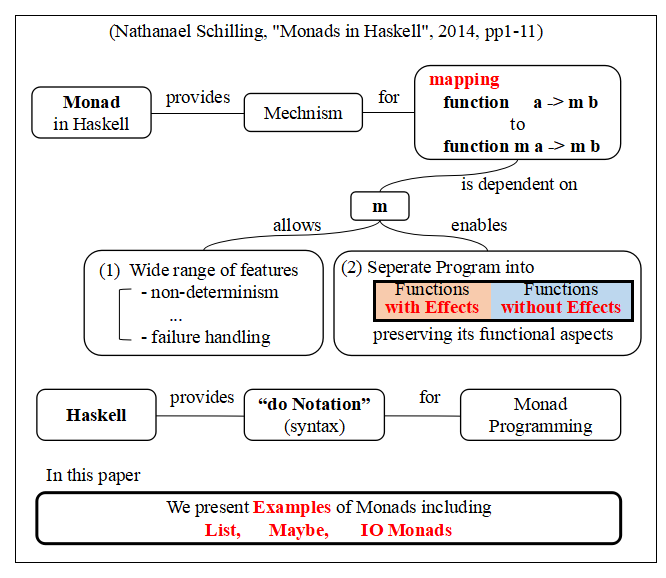
手元にある論文の印刷物を見ると，全ページにマーカーが引いてあり，読んだはずなんですが， 何がかいてあったのかはっきり思い出せません．全部にマーカーが引いてあるということは，きっと読みやすい論文だったのではないかと思います． あとで思い出したり，もう一度，読み直して，何が書いてあったか思い出したら，感想など書くかもしれません．
12ページの薄い論文ですが，論文全体が，これでもかというほど例で埋め尽くされています． 論文の構成は，
となっています．基本的に圏論が分かってないと読めません．それも Awodey の Category Theory + αが要りそうです．ただ，例が全部で３２個あります（すべてがモナドの例という訳ではありませんが）．ですから，圏論が中途半端にしかわかって無くとも，どんな例があるのかということをとりあえず，頭に入れるために眺めてみるという手もあるかもしれません．
あと，参考文献を見ると，この著者 Philip S.Mulry は，この分野の論文をたくさん出されているようなので，どれか易しそうなのを探して読んでみるというのも良いかもしれません．
第１０章（最終章）がモナドと代数（Monads and Algebras）です．ここでは，モナドが随伴関手の合成で 作られていること，また，モナドを随伴関手に分解できることが書かれています．モナドが どのように使われているかはこの本の範囲外です．といいますか，一般に圏論の本では モナドの扱いはこんな感じです．
第５章（最終章）Categories at work の第３節が 5.3 Monads となっていて，モナドの章です． この本は MIT Press から販売されていますが，古い版
David I. Spivak, "Category Theory for Scientists (Old Version)", September 17, 2013"は，PDF で Freely available です．
私はこんな感じで自家製本して，最近持ち歩き始めました．やはり書き込みが自由にできると思う
と結構気が楽です．この自家製本技術については，
製本 DO IT YOURSELFに書きましたので，もし，これを読まれている方が，あまり圏論を
深くは分かって無くて，モナドを勉強するのに先が長そうなら，こういう教科書を製本など
しながら，気楽に勉強していくというのはどうでしょう？
ここではモナドのことを書かないといけないんですが，まだ読んでません．パラパラと 見た感じでは，随伴関手の話だけではなさそうです．節の中のタイトルを拾っていくと，
となっていて，全部で14ページ弱あります．
ちょっと古い本ですが，2000 年にちょっとだけ手が入れられて，リプリント版が
Reprints in Theory and Applications of Categories, No. 12, 2005, pp. 1–288.から入手可能です．Copyrightは
TOPOSES, TRIPLES AND THEORIES
MICHAEL BARR AND CHARLES WELLS
Copyright 2000 by Michael Barr and Charles Frederick Wells.となっております．これも昨日（2017年9月22日）に
This version may be downloaded and printed in unmodified form for private use only.
Toposes, Triples and Theories の内容に示すような構造になっています．本自体は，Topos の話題が中心のようですが，モナドは 3章と9章で取り上げられています．また，3章の終わりには1ページくらいの Historical Notes on Triples があります．圏論の詳しい内容は分からなくとも， モナドにまつわる1984年までの動きはこれで少しわかるかもしれません．Moggi がモナドを プログラミング言語の Inpure な部分の構造化に使ったのは 1990 年前後ですから， それ以前の人の頭のなかの蓄積としては，ここに書いてあるようなことがあるのでしょう．
9章の節建ては
となっています．
圏論のお勉強へ