Survey and Study of Monads

There are topics about Monads in the Category Theory. For example, the chapter 10 of the text book by Steve Awodey, "Category Theory" is about Monads. In general, although text books in category theory describe that monads are compositions of adjoints and the can be decomposed to adjoints, etc., those text books do not tell the usages of monads.

On the other hand, since it is proclaimed that monads can encapsulate side effects in functional programming languages, like Haskell, preserving the functional features, many programmers are interested in the monads. The wikipedia says Eugenio Moggi began this usage of monads.

Moggi, Eugenio (1991). "Notions of Computation and Monads" (PDF). Information and Computation. 93 (1): 55–92. doi:10.1016/0890-5401(91)90052-4.

Other than this usage in the functional programming languages, monads seem to have many applications. Here, I am going to survey the usages of monads. I listed up the references I have read or am going to read below. I attached figures to some of them reading their abstracts. If you are interested in them, please read them by yourself.

- Topics about Functional Language and programming

1. Moggi, Eugenio, "Notions of Computation and Monads" , 1991, pp1-29

   I ought to have read it. I put a figure made from its abstract.

   

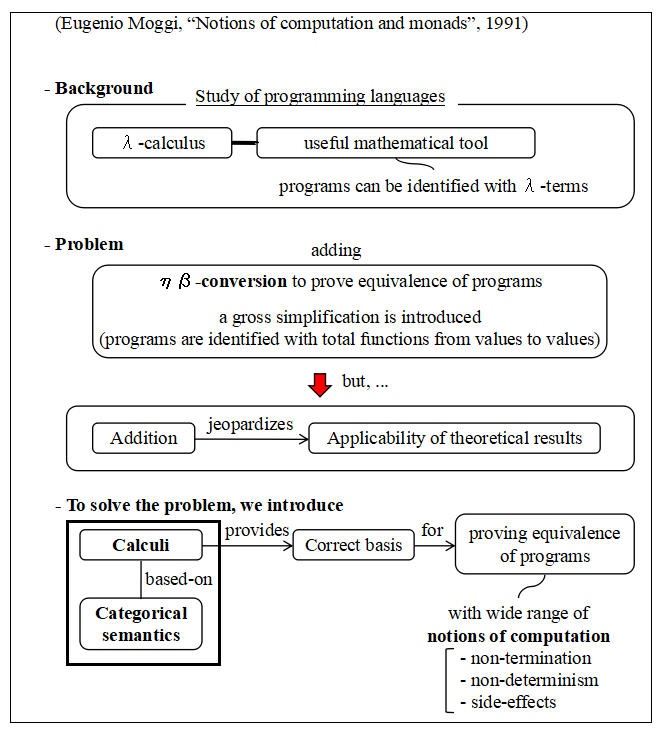
   I explain the figure to be sure.

   λ-calculus (lambda-calculus) is a useful mathematical tool for the study of programming languages, since programs can be described as lambda-terms.

   However, introducing the eta-conversion to enhance the power of proving the equivalences of programs, a problem arises, that is, applicability of theoretical results might be jeopardized.

   We introduce calculi based on category theory that provide a correct bases for proving equivalence of programs with wide range of notions of computation, non-termination, non-determinism, side-effects.

   Oops?

   Where did the eta-conversion go? I am sorry I did not catch the relation between eta-conversion and the wide-range of computation notions. If you are interested in it, please read the paper.

   The author presents several examples of monads concerning computation (Partiality, nondeterminism, side-effects, exceptions, continuations) in the first 5 pages. To understand the examples, the knowledge of category theory is requited, as the level of Awodey's category theory, or more (The knowledge of the concept "monads" is required. You had better read a text book which contains topics about monads beforehand even if the text is thin,

   In chapter 2, the author defines a simple programming language with monad features and provides a system to prove the programs written in the language. The rest of the paper is organized as follow.

   3. Extending the simple metalanguage
   4. Strong monads over a topos
   Conclusions and further research
   

2. Philip Wadler, "The essence of functional programming", 1992, pp1-23

   Phillip Wadler is one of the designers of Haskell.

   I put a figure made from its abstract.

   

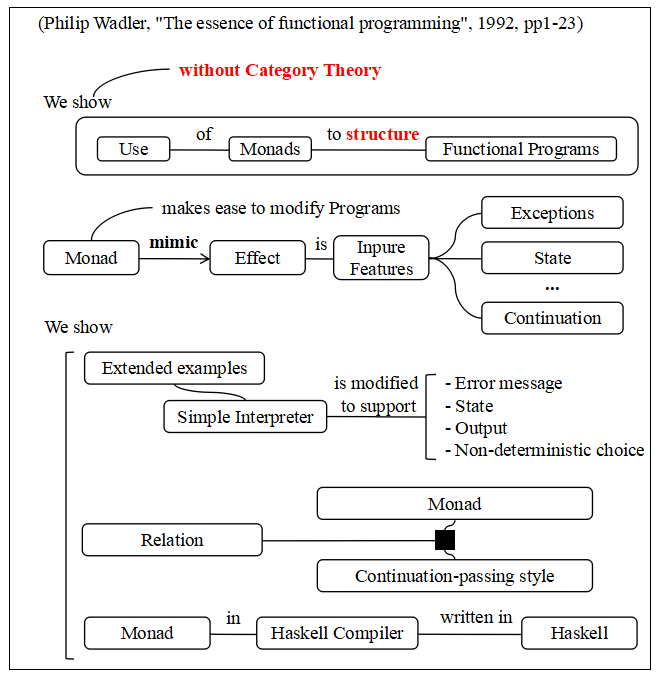
   It says the author explain the use of the monads to structure functional programs without category theory. The phrase "without category theory" is helpful to us, isn't it.

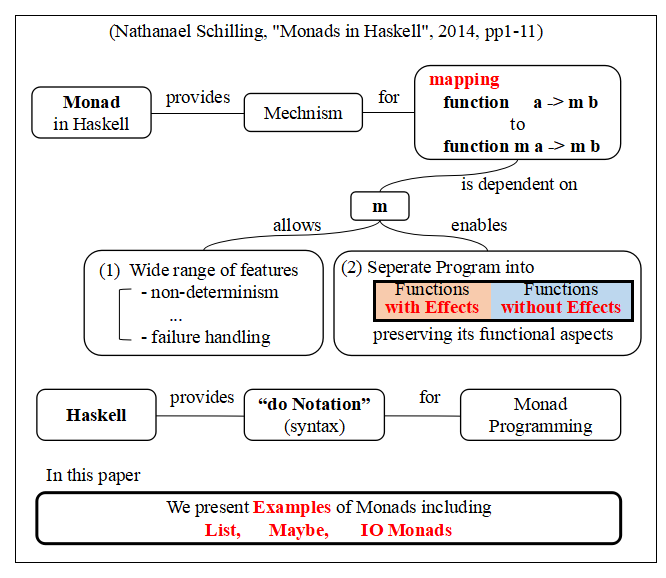
3. Nathanael Schilling, "Monads in Haskell", 2014, pp1-11

   I put a figure made from its abstract.

   I think this paper is easy to understand how the monads are used in Haskell.

   The monads in Haskell provide a mechanism of monads of mapping

   function a → m b to function m a → m b

   Here, the mapping is depentent on m (monad). The mechanism m allows wide range of features from non-determinism to failure handling and enables the separation of program into functions with effects and functions without effects preserving the functional aspects. Haskell provides "do Notation" for monad programming. This paper presents examples including List, Maybe, IO monads.

   For me, this paper is easy to understand. If you do not know how monads are used in haskell well, I recomend this paper first.

   

   - Topics in Computer Science

4. Philip S.Mulry, "Monads in Semantics", 1998, Pages 275-286

   While this is a thin paper of 12 pages, it contains a lot of examples. The paper consists of

   1. Preliminary definitions and examples (9 examples)
   2. Categories of Algebras (11 examples)
   3. The results and examples of "Lifting Tools" (12 examples)

   Basically, to read the paper, the knowledge of category theory (at he level of chapter 10 of Awodey's text book) is necessary. Though, since there are 32 examples, simply viewing them would be useful even for the readers who do not know the category theory well.

   Since there are many references to the author's own papers, it would be good to seek some paper that matches the reader's interest.

   - Other applications

5. ... I am looking for some good references for other applications ...

   - Fundamental text books, tutorial, paper about monads

6. Steve Awodey : Category Theory

   The chapter 10 (the last chapter) is about the monads and algebras. The chapter explains the composition of left and right adjunctions is a monad and, conversely, a monad can be decomposed into left and right adjoints. The usages of monads are out of topics. In general, usual text books of category theory do not step into such topics.

7. David I. Spivak: Category Theory for the Sciences, 2014

   Topics of monads are in "Section 5.3 Monads" in the last chapter (chapter 5) of the book. Though this book is published from MIT Press, the PDF of its previous version is available freely at

   David I. Spivak, "Category Theory for Scientists (Old Version)", September 17, 2013"

   
   I bound the printed papers into a book by myself as the right picture and began to carry the book recently. The book I can write freely is comfortable for self study. I wrote the method of binding into a book at Binding Books by Yourself (Japanese). If you are interested in such comfortable text book, please refer to the page.

   I should write about the contents of book instead binding books. I have not read the section. As long as I roughly see the section, it seem to include topics other than adjoints. The titles are

   • 5.3.1 Monads formalize context
   • 5.3.2 Definition and examples
   • 5.3.3 Kleisli category of a monad
   • 5.3.4 Monads in databases
   • 5.3.5 Monads and adjunctions

   and 14 pages in total.
   

8. M. Barr, C. Wells, "Toposes, Triples and Theories", 1984

   The book is a little old. But, its reprint version (2000) with a little change is available at

   Reprints in Theory and Applications of Categories, No. 12, 2005, pp. 1–288.
   TOPOSES, TRIPLES AND THEORIES
   MICHAEL BARR AND CHARLES WELLS

   The Copyright tells

   Copyright 2000 by Michael Barr and Charles Frederick Wells.
   This version may be downloaded and printed in unmodified form for private use only.

   I bound this book yesterday(22nd Sep. 2017) by myself too.
   The 'Triples' in the title are Monads. Monads have many names, Triples, Standard constructions, fundamental construction, Monads．The last 'Monads' was given as a standard name later. The contents of the book are

   The contents of "Toposes, Triples and Theories"

   While the main topics is Topos, the topics of monads are in chapter 3 and 9 too. Chapter 3 has the section Historical Notes on Triples (1 page). It will provide the movement till 1984. Moggi used monads to structure programs in functional programming languages around 1990. Thus, the section provides the knowledge in the researchers before his proposal.

   The chapter 9 consists of

   • Duskin's Tripleability Theorem
   • Distributive Laws
   • Colimits of Triple Algebras
   • Free Triples

   
   

Let's study category theory (japanese)

Homepage Top(Japanese)