
Steve Awodey : Category Theory

圏論の教科書としてはかなり定評のある本です.
この本に対して,私は,自分で勝手に右のような感じの表紙をつけて,持ち歩いています.
ちなみに,この絵は,随伴関手(Adjoints あるいは, Adjunctive functors)をなんとなく カッコよく描いてみたつもりのものです.
もうひとつ,ちなみに,一般にプリントアウトしたものを持ち歩くとき 簡単にでも製本すると気持ちが良いです.このような簡易製本のノウハウを 製本 DO IT YOURSELFに書きましたので,ご興味が あればそちらもどうぞ.
Awodey の本の 2006年版は,Awodey 自身の site の ここの一番下の
Weekly lecture notes are here.のリンクをたどったところから見えるようです.
Awodey 先生の圏論の講義は Youtube にも動画がアップロードされており, そのプレイリストが
https://www.youtube.com/playlist?list=PLGCr8P_YncjVjwAxrifKgcQYtbZ3zuPlbに作成されているようです.この本は,一応,簡単,かつ,きちんと書かれた本として 定評があります.上のLogic Matters : Category Theorydでも,「世の中には沢山のテキストが あるんだけど,とにかく2つ挙げさせてもらうと,このAwodeyの本と Leinster の本だ」と 書いてあります.
では,以下,目次に従って各章の扉のところの説明をまとめて行きましょう.
圏の例は結構沢山紹介されていて,全部で13個あります.
他の本もですが,圏の例が 沢山紹介されている本が多いです.つまり例がとても大事なんですね.悲しいかな, 数学専攻以外の読者にとってはあまり例がぴんときません.「群? ベクトル空間? 位相? 何? それ,おいしいの?」 ってな感じですよね.
でも,計算機科学側の学習者としては,例として,論理式の集合や関数型プログラミング言語が あるのは嬉しいですよね.
あと,注意として, 前順序(Preorder)と半順序 (Poset) は,そういう構造を持った集合の集まりの圏じゃなくて, 1つの集合そのものが圏になります.つまり,その集合の要素がオブジェクトになり, 要素 x, y に順序関係が あるとき,形式的にx から y に射が1つあるとしたものです.最初は,圏の例を 示すために無理やり持ってきたように見えますが,これらは圏というものの構造の一端を担う とても重要な圏です.あとの方で圏論の最高峰として随伴関手(Adjoint Functor)という ものがでてきますが,これを前順序で解釈したものがガロア接続(Galois Connection)です. ガロア接続は,代数学のガロアの理論の一番外側の骨格になっているだけでなく, 形式的概念分析 (Formal Concept Analysis),プログラミング言語の抽象解釈 (abstract interpretation)などに使われます.
あと,「1.6 CONSTRUCTIONS ON CATEGORIES」 は,しっかりやっといてください.すでに
存在する圏(あるいはいくつかの圏)から新しい圏を作る方法ですが,
そこに出てくる
次に続きます.二章以降は,章直下の概要説明があるようですから,それを 記述していきます.
今,全体をざっと読んでみました.Awodey 先生は,章はじめの 概要にあまり,具体的な内容を書かない人みたいなので,書いてあることを そのまま載せても分かりにくいような気がします.ということで, 目次などから適宜キーワードを拾って,補いながら書いていきます.
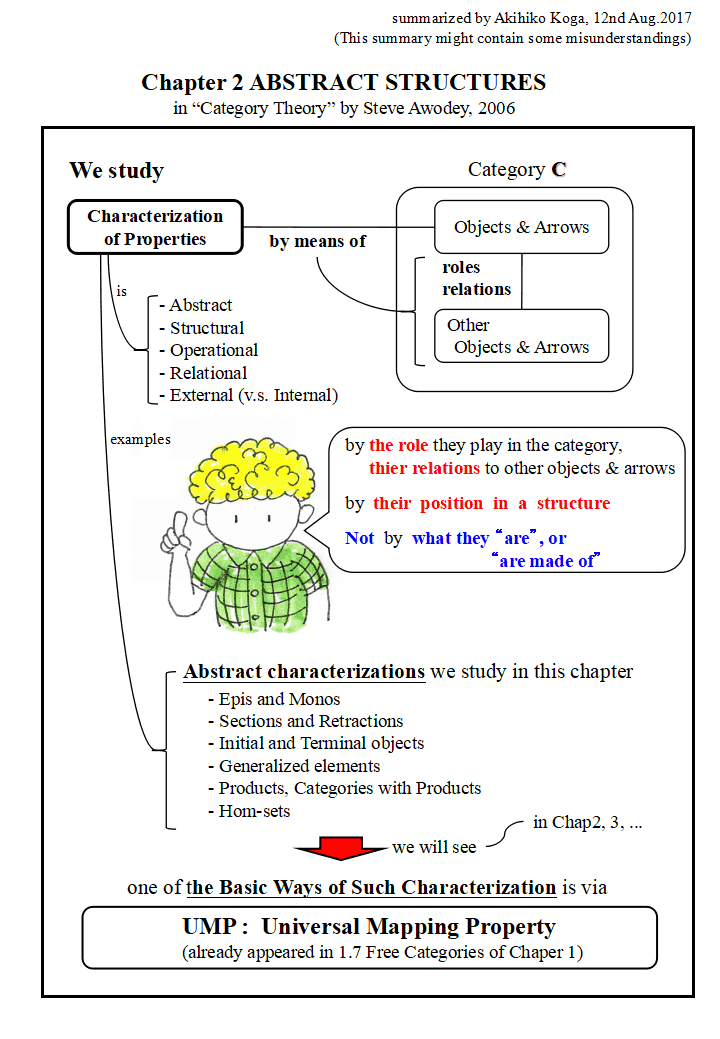
ここでは,記述されるオブジェクトや射が演じる役割と他のオブジェクトや射との関係 (the role they play in the category, thier relations to other objects & arrows)が 重要で,それらが「何であるか?」あるいは「何で出来ているか?」(what they "are", "are made of")は重要ではありません.こういう特徴づけは,Abstract, Structural, Operational, Relational, External (v.s. Internal)であるということができます. この章ではこのような特徴づけとして,
という 性質です.簡単なところで似た概念を探すと(本当は「似ている」のではなく本質的に同じなのですが),与えられた条件を満たすオブジェクトと射のうち最も一般的なものが(同型を除いて)一意に決まる
がイメージを掴みやすいと思います.順序集合(Poset : partially ordered set)では,最大の要素は存在すれば一意に決まる. (前順序集合(Pre-ordered set)では,同値を除いて一意に決まる)
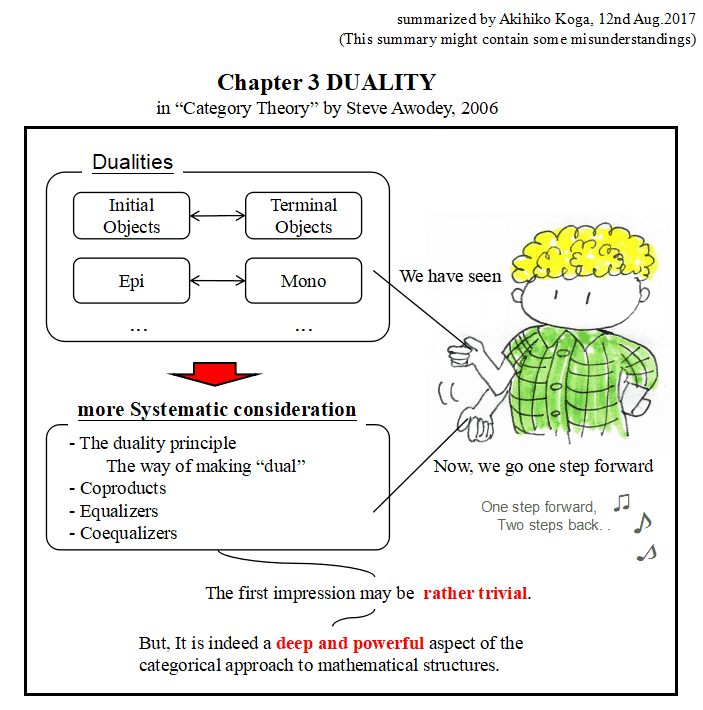
これらは射をひっくり返しただけなので,最初はとても当たり前(trivial)に
感じると思いますが,結構,
私の経験でも,実際,射をひっくり返しただけでこんなに元の概念と変わってしまうのか と驚くことが多いです.特に,関数の概念は多:1で(つまり,相手が一つに 決まればよいので),射の元と先で対称性を持っておらず, 双対をとると容貌が変わってしまいます.例えば,集合と関数の圏 Sets ではinitial object は 空集合でただ1つしかないのに,terminal object は singleton set (ただ1つの要素から なる集合)で無数にあります(すべて同型ですが).これに対して,関係(relation)を射に とれば,initial object も terminal object も空集合です.
圏論から離れて,例えば, 半群論で,関数の半群 S ⊆ (A→B) では右ゼロは簡単に作れるのですが, 左右を入れ替えた左ゼロはちょっと考えないと難しいです(A, B は集合,A→B はAからBへの 関数の集合とします). 実際,右ゼロとなる関数はAのすべての要素をBの同じ1つの要素 b に飛ばせば,それが 右ゼロですが,左ゼロの関数 f を作るためには,すなわち,その関数の適用のあとに別の関数を適用しても結果が変わらないようにする(f∘g = f for ∀g∈S)ためには,考える関数 の集合 S を予め制限しなければなりません.もしこの例が分かりにくかったら忘れてください.
ここでは次の3つの観点から,群論と圏論の関係を考察します.
まず,Groups in a Category は圏の中に群を構成する方法です.有限積のある圏を とり,その圏の中のオブジェクトGが群であることを記述するために, 単位元 u : 1 → G, 2項演算 m : G×G → G, 逆元をとる1項演算 i : G → G を 持つことを課し,さらにそれらが群の公理(結合法則を満たす,単位元がある, 逆元がある)を満たすことを課します(普遍代数っぽいです).これは, 圏の中にこのような演算を持つ体系を表現する常套手段みたいです.
次に the Category of Groups は,以前に例として示した,群をオブジェクトとし群の準同型を 射とする圏の中で,群論の基本的な概念(準同型 h に対するカーネル ker(h)など)を 表現する方法です.ここでは例えば,equalizer が カーネル ker(h) になることが示されます.
最後に,Groups as Categories ですが,これは群論での商群を作ったり, カーネルを求めたりといった操作が,圏の圏(圏をオブジェクトとして関手を射と する圏)にも適用することができるということを学びます.例えば,群論の中で 行うように,圏の圏の中でも,商圏やカーネル圏が作成できることが示されます.
この章の概要の最後で,「もしあなたが,すでに群論の基礎的な知識があれば, ここでやっていることを 見ることですでに学習した1章から3章までの深い洞察を得ることができる だろう」と言っています.さらに,「もし,群論を知らなくても,ここで圏論を 応用して群論を学べば良い」と言われています.本当に,群論の基礎を知らなくても この章を読んだだけでそれを学習することが出来るかどうかは分かりません.私は,分からなかったら, この章は雰囲気だけ掴んで,気にせず,次の章に行ったら良いと思います.確か, この本でも,また, Leinster の本でも,「例は全部分からなくても気にするな」と 書いてあったと思います.
まず,図の上部 We start with Brief Discussion と書いてある箱を説明します. 第5章の最初では,まず,今まで学習したこととその延長のような概念,Equalizer, Monic, Generalized elements, Subobject, Pullback などの概念を使って, 数学における,すでに皆さんが知っている概念を表してみます. Pullback は,あまりなじみがない人もいるかもしれませんが,Awodey の教科書に よると,数学や論理学で頻繁に現れるとても重要な概念で,Product を少しだけ 複雑にしたものです.また,ここで表す数学上の概念としては,一つは部分集合, 部分群,部分代数など,部分の概念で,これは Monic で表します.もう一つは, 逆写像や共通集合,あるいは,それらを合わせたような概念で,これを Pullback が 担当します.
また,教科書の前半では,Product, Equalizer, Pullback, Terminal Object などの重要な 性質もみていきます.それは
圏にProducts とEqualizers があれば,Pullbacks と Terminal Objectsも 存在するし,逆に Pullbacks と Terminal Objectsがあれば Products と Equalizers も 存在する.という性質です.先回りして言うことになりますが,この性質がなぜ重要か説明しておきます. この章ではいままで述べたような Pullback などの概念を一般化した Limits と Colimits を説明 するのですが,Limits は Products と Equalizers が あれば作れるのです.したがって, それら二つの代わりに,Pullbacks と Terminal Objects があっても,やはり Limits を作れることになります.上の性質は,こういう Limits を作れる条件に 関係してくるのです.ちなみに, Colimits は, Coproducts と Coequalizers があれば作れます.
これらの Brief Discussion を十分楽しんだあとに,よりシステマティックに, このような概念の定義に取り組んでいきます. General Notion of "Limits and Colimits" と書いてある2番目の大きな箱の中を 説明していきます.
Limits/Colimit の概念は圏の中の与えられた図式を満足するオブジェクト(と射)の 中で UMP (Universal Mapping Property) を満たすもののことを言います.ここで図式と言っているのは,圏の中の いくつかのオブジェクトとそれらの間のいくつかの射を選んだものです. あるオブジェクト C からこれらのオブジェクトへの射が可換であるとき,C は その図式の Cone であると言います.
上で私は,オブジェクト C からの射が図式と可換であることを「図式を満足する」と表現 しましたが,実は図式は,オブジェクトと射に対する条件を表しています. 等式で表される条件ですし,一般には複数のオブジェクトと射が絡みますから,連立方程式みたいな条件です.で,Cones の集合は, その図式の条件を満たす解の集合に相当します.その中の UMP を持つオブジェクトは 解の中の最も一般な解を表します.ちょっと直観的,かつ,荒っぽい説明でしたので, 正確には教科書を読んでください.ただし,このような直観を持っておくことは 役に立つと思います.
Colimits については,Limits の Dual をとったものです.
以上,説明してきたものが Limits と Colimits で,これらの例としては今まででてきた,Product, Coproduct, Equalizer, Coequalizer, Pullback, Pushout, などがあります.
あとは,Limits と Colimits に関する話題がいろいろ展開されています.まず,さきほど言った, Product と Equalizer があれば,Limits は作れること. それから極限を保つ関手のこと.これは色々な応用がありますが, 上の図に書いてあるような同型式などを簡単に証明できるようになります. もう一つの話題は極限を作る関手ですが,これは変換した先の圏で極限が あれば,その逆像,つまり出発点側の圏にも極限があるような関手で, 群論などでの議論を忘却関手(Forgetful functors)を使って,集合の圏の 議論に帰着させることができます.
これが本章の概要ですが,章直下の概要説明には,続きが書いてあって, この章の後,第6章で,もう一つだけ基本的な概念(Exponentials)をやった 後,第7章(Functors and Naturality)で,いわゆる, "Higher Category Theory" と 呼ぶべきものに進むので楽しみにしているようにと書いてあります.
でも,私は,この章の内容も,次の章の内容も楽しいです.とくに次の章は Exponentials で, これは関数の空間や論理学の「ならば」(A -> B)を作ることに関係していて, 応用上も重要です. そのことを こそっと上の絵の中にも書きました.
これでこの章の概要説明は終わりです.
最初に,この章の概要で位置づけについて自信がないと言いました.これは, 最初の Discussion の部分で,数学上の部分集合や逆写像を Monic や Pullback で 表すところがあるのですが,これは単に,Limits/Colimits の具体例となる概念が 重要であることを示すためだけなのかどうかが自信がないのです.それだったら Limits/Colimits の章でなく別の章で圏による数学上の概念の表現の有用性の 説明の章を設けても良いように思えるし,第一,Monic がすぐ,極限と結びつかない など色々疑問がわいてくるのです.解説文の中に疑問を色々挟むのは 読者に対して不親切で,申し訳ないです.でも,本当によく分からないので,正直に 書いておきます.
でも段々長くなってきたなあ.1ページに収まるかなあ?
前章まで, Equalizers, Products, Pullbakcs など,多くのUMPを表す概念をLimits/Colimitsという
概念になんとか統一してきました(1).でも,Free Alggebras はまだです.
これは, Limit/Colimits より深いところにある Adjoints という考え方に
よらなければ統一的な扱いはできません.これは9章でやります(2).
この章では,(3) の,Limits/Colimits で統一できないもうひとつの
概念の
この章のトピックスとしては以下の通りです.
結構,もりだくさんで,Exponentials は使いでがありますよね.
(圏論に携わっている)数学者にとって,Natural Isomorphism という概念の比重が,私たち 門外漢に比べてとっても大きいのではないかということでした.私が混乱したのは,「ここはNatural Transformation」の 章なのに何で Natural Isomorphism ばかり書いてあるんだ」ということでしたので.たぶん, とても重要なのでしょう.

この章は,最初に,圏の圏の性質がいくつか(Product, Coproduct, Equalizer を持つなど )の レビューがあって,次に関手についての基本的な用語を定義します.injective/surjective on objects/arrows, と faithful, full です. 特に, faithful, fullは重要です.injective/surjective on awwors との区別を しっかりつけておきましょう.本文中にも,faithful と injective on arrows を区別する例が載っていますが,ここでもちょっと人為的だけど直観的に分かると思われる図を載せておきます.
次にこの章の動機付けの例を2つ,詳しく見ていきます.Hom functor と Stone duality です. これらは Natural Isomorphism を理解するための例だと思って読んでください.
その後で,Natural Transformation の定義がなされて,それによって
これらのもとに,色々な関手の圏やMonoidal 圏の定義の仕方,圏の同値関係の概念を学びます. 特に,ここで定義する圏の同値関係は,2つの圏が同型ではないのだけど,ほとんど同型といった ,より広い同値関係を導入しますので,圏を理解するのに有用です.この圏の同値関係は 第9章で学習する随伴関手(Adjoints)の特殊な例になっています. ということでも,この章は大事ですし,次の8章から最後までの基礎になっていますから, この後ろの章で分からなくなってきたら,この章を読み直すのが良いと思います.
あと,圏論の圏論を考えるわけですから,これらの中にはいわゆる「Abstract Nonsense」に 見えるものもあるわけですが,これらは,実際に我々の手元にあるそれぞれの 特殊な問題に具体化することができる一般的な圏であり,決して「Abstract Nonsense」では ないよとも言っています.
「米田のレンマはとても有用なテクニックで, 圏論の中で単独で用いられる結果の中ではもっともよく用いられるレンマだ. Amzing ! いったい,何度現れるのだろう?」と 書いてありました.と言うか,扉の説明にそれしか書いてなかったので, 読者には,Awodey が感激していることだけが分かって,この章で具体的になにを やるのか見当がつかなかったんじゃないかと思います.この部分は後で修正されて, Amazing ! の部分が落とされて,章の具体的な内容が少し入りました(個人的な希望としては Amazing ! は 残しておいてもよかったように思います). あと,この米田のレンマは,群,半群(モノイド)での Cayley の定理や, 順序集合の,冪集合(Powerset)や順序イデアル(Order Ideals)による表現の 素直な拡張になっています(それらも表現定理です).
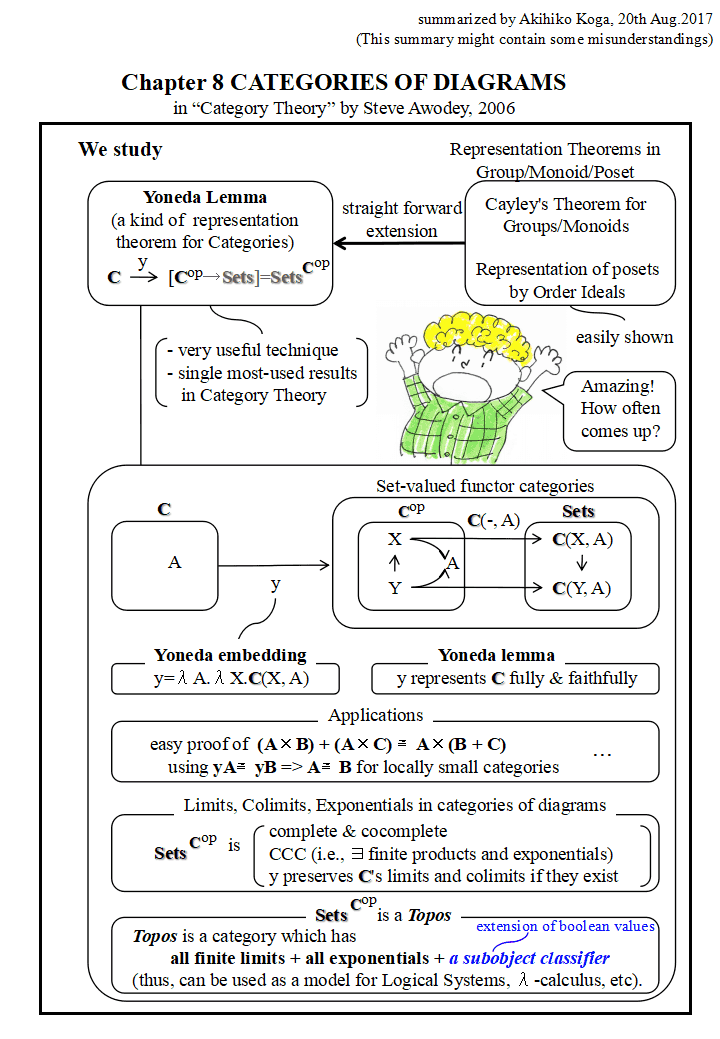
で,この章の内容は,
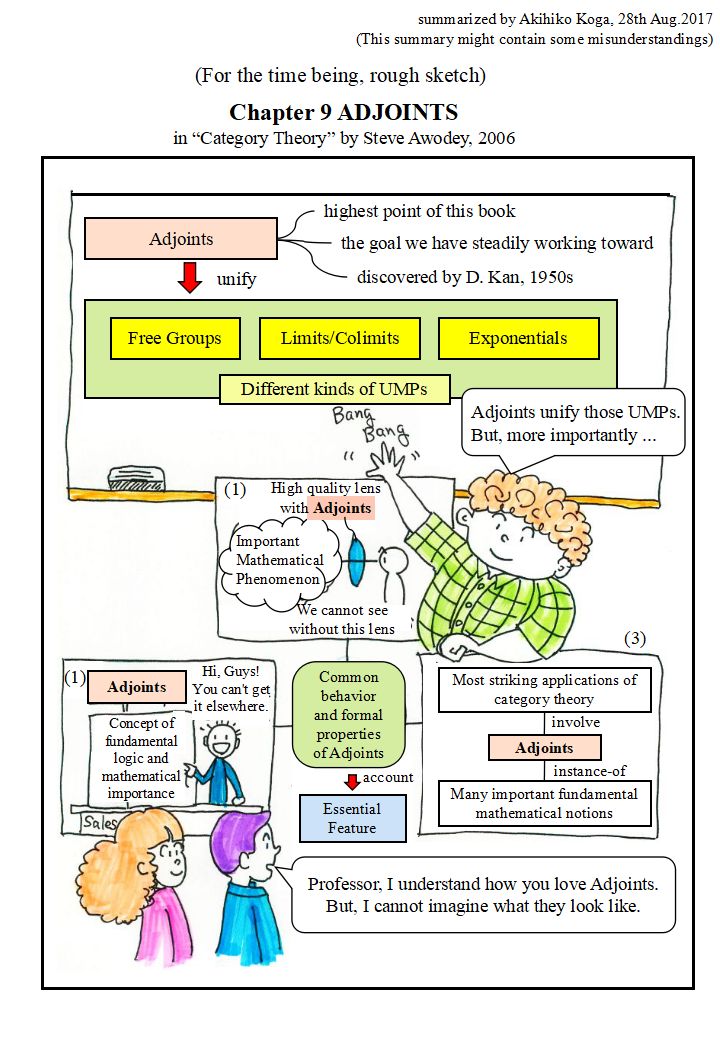
これが「当面」なのは,次のような 必要な情報がまったく入ってないからです.
これらを考えながら読めば良いのかもしれませんが,私が欲しい 「先行オーガナイザ」の役割を 十分果たすためには,多少のキーワードは入っていて欲しいと思います. 今のところ,これらを多少でも書き加える積りですが,いつになるかは分かりません. これをおいておき,他のものにとりかかるかもしれません.
一応言っておくと,Adjoints は2つの圏から相手に向かう関手があり, それらがある関係を持つことで相互に拘束しあっている関係です.
一言不満を言うと,私としては この説明の仕方よりは,それぞれの圏が,ある共通の骨格の圏とある関係に なっているという説明が分かりやすいと思うのですが,そういう説明を陽に している本は見たことがありません.調べ方が足りないのか,やっぱり, 一般の本のような Adjoint の説明の仕方の方が良いのか.
ここでは,まず,等式の集合で規定される代数 T-Algebra の圏から集合の圏への 忘却関手 U の left adjoint として,T-Algebra の Free 関手の存在が 保証されることが,前章の Adjoint Functor 定理から導かれるということを 思い起こします.
次に「モナド」を,ある種の代数系を規定する自己関手 T : C→C として定義し,モナドが Adjoints と深い関係を持っていることを示します. つまり,F -| U という Adjoint があるとき,T = UF とおけば,T はモナドに なり,また,T から Adjoints の組 F -| U を構成する方法がある(Eilenberg-Moore の方法とKleisli の方法)ことが示されます.モナドの例としては, closure operation (位相空間で集合に対して,それを含む最小の閉集合を割り当てる 演算など),集合のパワーセットを割り当てる関手,自由モノイドを割り当てる関手 などがあります.
この章では,モナドでない自己関手 P : S → S から代数系を作成 する方法についても解説され,最後に,その代数系がモナドになるための条件も 示されます.
この章では,モナドが Adjoints と相互に変換しあえる関係であることと 自己関手からの代数系とモナドの関係だけが述べられ,モナド自身や自己関手を 使った代数系がどのように使われるかは載っていません.
これでこのテキストは終わりです.あとは,このテキストで身につけた基礎を 頼りに,荒海にのりだすか,あるいは,もっと専門的な本を読むかということ なのでしょう.
ということで,Awodey の Category Theory の解説もこれで終わります.
圏論のトップページ