One page explanations for the chapters of
Awodey's Category Theory

Back to "Let's study category theory"
Related page : short explanation of Leinster's "Basic category theory"

This is a very good book, maybe easier than Mac Lane's "Categories for the Working Mathematician", still, full of rich topics and examples of the category theory, especially, in computer science.

?

The text book (2006 Version) can be accessed at

Weekly lecture notes are here.

- One page Explanations

PDF of the one page explanations is here

1. Chapter 1 Categories
   (None. No short explanetion at the front page of chapter 1.
   So, I did not make a figure for the contents of the chapter 1.)

   Maybe, UMPs (Universal Mapping Properties) are hard to understand for the first time. But, they are very important concepts through out the whole text. So, I recommend to study them again and again when you feel some troubles about the explanations involving UMPs. To imagine the following fact in our mind is useful to understand UMPs.

   For a subset A of poset P, a maximum (minimum) element of A is uniquely determined if A has.

   In addition, slice/coslice category, arrow category, a poset as a category (not Posets), a preordered set as a category are important more than novice leaners may think.

2. Chapter 2 Abstract structures
   In chapter 2, we study how to express several concepts (such as epis and monos) about objects and arrows categorically, that is, by the relations to other objects and arrows. This is the part written as "Characterization of Properties" in the following figure.

   
   

   Here, roles and relations of objects and arrows to other objects and arrows are important, and "what "they" are" or "what they are made of" are not important. Such characterizations are "Abstract, Structural, Operational, Relational, External (v.s., Internal). In this chapter, we study the following concepts as such concepts.

   • Epis and Monos
   • Sections and Retractions
   • Initial and Terminal objects
   • Generalized elements
   • Products, Examples of Products, Categories with Products
   • Hom-sets
   Through the study of the above concepts, we will see one of the basic ways of such characterization is via

   UMP: Universal Mapping Property

   "UMP: Universal Mapping Property" has already been introduced in chapter one (1.7 Free categories). But, many readers would have not recognized the concept was so important at chapter one. I recomend readers read the part "UMP" appeared in 1.7 repeatedly.

3. Chapter 3 Duality
   Here we will continue to see "abstract characterization". Especially, we will see the concept "Duality", that is, to construct concepts by reversing arrows. We have already seen "Initial" v.s. "Terminal" and "Epi" v.s. "Mono". In this chapter, we study such pair of concepts more systematically.

   
   

   Since the dual concepts are build by reversing arrows simply, readers might think the concepts built by such operations are trivial. But it(dualization) is indeed deep and powerful aspects of categorical approach to mathematical structures.

   Indeed, some dual concepts seem very different from their original concepts. For example, in the category of sets, the arrows(function) are not synmetric along the direction. In the category Sets, while there is only one initial object, that is, the empty set., there are many terminal objects, that is, singleton sets. The product and coproduct (disjoint union) of Sets seem very different too.

4. Chapter 4 Groups and categories
   We will study varous connection between groups and categories.

   
   

   We will focus on three different aspects.

   1. groups in a category
   2. the category of groups
   3. groups as categories

5. Chapter 5 Limits and colimits
   Chapter 5 is about limits and colimits. The scene around us became category-like gradually.

   We start with two topics. One is representing mathematical concepts such as "subsets", "subgroups", "inverses", "intersections" in terms of category theory. To be more specific, we look categorical concepts "subobjects", "equalizers", "generalized objects", "pullback", "products". The other topics is seeing when we have products and equalizers in a category, we also have pullbacks and terminal objects in the category, and vice versa. These topics are integrated into the theory of limits/colimits in the latter half of the chapter.
   
   

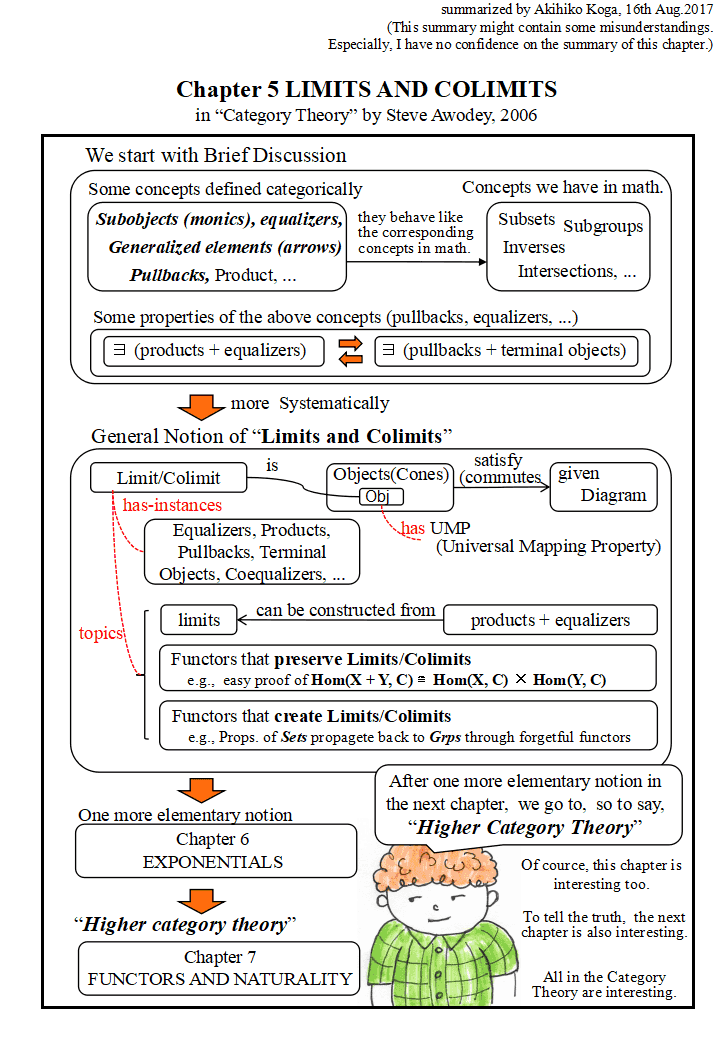
   In the latter part of this chapter, limits/colimits are defined as objects which have UMP concerning given diagrams of objects and arrows. "Equalizers", "Products", "Pullbacks", "Terminal objects" are their instances. As topics of limits/colimits, the followings are shown.

   • when we have all products and equalizers, we can construct limits using them.

   • functors preserving limits/colimits.
     we see that using such functors we can easily prove, for example,
     Hom(X+Y, Z) is isomorphic to Hom(X, Z) × Hom(Y, Z)

   • functors that create limits/colimits
     Using the property of such functors, for example, we can see some properties of Sets propagate back to Grps through forgetful functor U : Grps → Sets.

6. Chapter 6 Exponentials
   Exponentials are important. For example, Cartesian Closed Categories (CCC), which are categories with all finite products and all exponentials, act as models for Heyting algebras, Lambda calculus, etc. in computer science.

   
   

7. Chapter 7 Functors and naturality
   
   For me, this chapter was difficult to grasp the structure of the contents, the role of each section. Herhaps, the importance of the "natural isomorphisms" is much heavier for mathematicians than for me.

   In this chapter, first, some terminologies about functors, such as full, faithful, etc. are defined. Especially, the difference between fathful and injective on arrows is important. While an example of their difference is shown at the chapter, I add the another artificial example of their difference. It would be intuitive.

   

   In this chapter, we study the construction of Fun(C, D), the category of all functors from a category C to another category D with arrows natural transformations between functors. This category is very important.

   Now, I began to make the short explanation of "Chapter 9 Adjoints" and reallized the importance of this chapter "Naturality". If you feel difficulties in Chapter 8-10, it would be a good idea, to read this chapter again and again.

8. Chapter 8 Categories of diagrams
   
   

9. Chapter 9 Adjoints
   For the time being, I put the following rough drawing which is written by the short explanation at the front page of chapter 9.

   

   It is temporarily because it lacks the following necessary information.

   1. What are the "Adjoints" ? (Definitions or something like that)
   2. What is the mathematical phenomenon which cannot seen without the lens of category with adjoints ?
   3. What is the fundamental logic & mathematical importance ?
   4. What are the Most striking Categopry Theory Applications and how adjoints are involved ?
   5. What are the mathematical notions which are instances of adjoints ?
   6. What are the common behaviors and formal properties of adjoints ? What are the accounted essential features ?
   While it may be enough that we read this chapter thinking the above, I want some keywords indicating the above items in the summary drawing which I expect as "Advance Organizer" of this chapter.

   Now, I am going to rewrite the figure. But I have not decided when I will do it. I may do other work first.

   By the way, Adjoints means the situation that given two categories and functors from each category towards the other satisfy some conditions and they restrain each other.

   I think this is the usual explanation. But I do not like this. I think we should focus on the common skeletal structure of the two categories.

10. Chapter 10 Monads and algebras
    This is the last chapter of this book.

    

    After some preliminaries, "Monad", which represents a category of certain algebras, is defined as a endofunctor

    T : C→C

    with two natural transformations satisfying unit and associative laws.

    In this chapter, the relationship between adjoints and monad is explained, that is,

    - If these is adjoints F -| U, T = UF is a monad, and,

    - If there is a monad T, we can construct adjoints F -| U such that T = UF by Eilenburg-Moore method or Kleisli method.

    In this chapter, another category of algebras P-Alg(S), which is generated by an endofunctor

    P : S → S

    is also explained. P-Alg(S) is not always a monad. The condition for that P-Alg(S) is a monad, is shown.

Some links in my web-site related to this page (English)